图形学之卷积滤波器
博客目录：
一、盒式滤波器
二、帐篷式滤波器
三、高斯滤波器
四、三次B样条滤波器
五、三次 Catmull-Rom 滤波器
六、三次Mitchell-Netravali滤波器
当有了卷积工具，下面介绍图形学常用的几种滤波器：
一、盒式滤波器
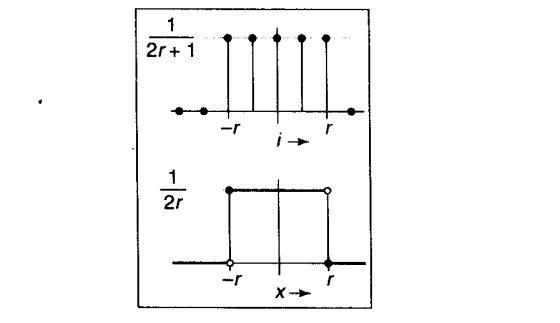
盒式滤波器是一个分段常值函数，它的积分结果为1。
- 离散滤波器，其数学形式为：
\[a_{box,r}[i] =
\begin{cases}
1/(2r + 1) & |i|\leq r\\
0 & \mbox{其他}
\end{cases}
\]
为了保持对称性，函数定义包含了两个端点。
- 连续滤波器数学形式：
\[f_{box,r}(x) =
\begin{cases}
1/(2r) & -r \leq x <r \\
0 & \mbox{其他}
\end{cases}
\]
此时只包含一个端点，使得半径为0.5的盒子能用作重构滤波器。因为盒式滤波器不是连续的，需要格外注意这些边界情况。
二、帐篷式滤波器
帐篷式滤波器（也为“线性滤波器”），是分段连续的线性函数：
\[f_{tent}(x) =
\begin{cases}
1 -|x| & |x|<1 \\
0 & \mbox{其他} \\
\end{cases} \\
f_{tent,r}(x) = \frac{f_{tent}(x/r)}{r}
\]
帐篷式滤波器没有值的跳变情况，不需将离散和连续情况分开。通过缩放标准大小的帐篷式滤波器\(f_{tent}\)来定义 \(f_{tent,r}\)。如果定义了滤波器\(f\),那么就可以用\(f_r\)来表示“滤波器伸展\(r\)倍（收缩\(r\)倍）”。但是\(f_r\)与\(f\)有相同的积分效果，并且积分结果等于1。
三、高斯滤波器
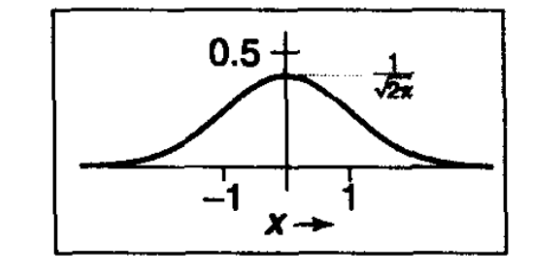
高斯滤波器（也称“正态滤波器”），没有有限支撑集（定义域\(-\infty \rightarrow +\infty\)）,必要时可将函数进行截尾处理，将某个半径之外的值都设为0。高斯滤波器因为其平滑的特性，是一种不错的采样滤波器。
四、三次B样条滤波器
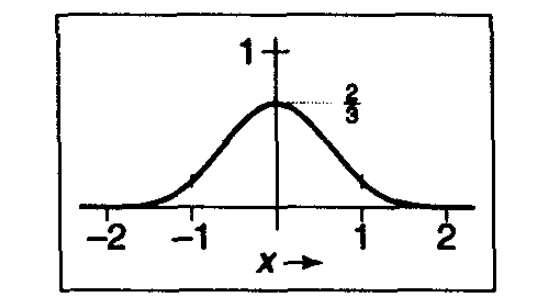
三次滤波器有4段，经常被用作重构。这种也被称为B样条滤波器，起源于作为样条曲线的混合函数：
\[f_{a}(x) = 1/6
\begin{cases}
-3(1-|x|)^3 + 3(1-|x|)^2 + 3(1-|x|) +1 & -1 \leq x \leq 1\\
(2-|x|)^3 & 1 \leq |x| \leq 2 \\
0 & \mbox{其他}
\end{cases}
\]
五、三次 Catmull-Rom 滤波器
这是另一种三次滤波器，如图在x=-2 、-1、 1、 2处函数值为0，可用作重构滤波器插值样本。数学表达形式：
\[f_{C}(x) = 1/2 \begin{cases}
-3(1-|x|)^3 + 4(1-|x|)^2 + 3(1-|x|) +1 & -1 \leq x \leq 1\\
(2-|x|)^3-(2-|x|)^2 & 1 \leq |x| \leq 2 \\
0 & \mbox{其他}
\end{cases}
\]
六、三次Mitchell-Netravali滤波器
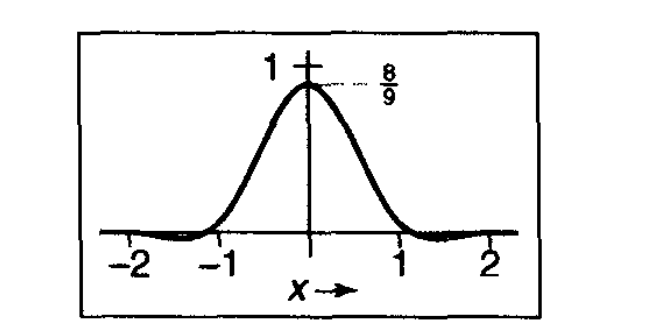
三次Mitchell-Netravali滤波器用于解决重采样图像问题，在上述两种三次滤波器中折中改进，这种滤波器是前面两种滤波器的加权组合。上图的数学表达式：
\[f_{M}(x) =\frac{1}{3}f_{B}(x)+\frac{2}{3}f_{C}(x) = \frac{1}{18}
\begin{cases}
-21(1-|x|)^3 + 27(1-|x|)^2 + 9(1-|x|) +1 & -1 \leq x \leq 1\\
7(2-|x|)^3-6(2-|x|)^2 & 1 \leq |x| \leq 2 \\
0 & \mbox{其他}
\end{cases}
\]
