图形学中的数据结构
在图形学中涉及多种数据结构,下面介绍三种常见的数据结构:
一、翼边数据结构( Half Edge)
翼边数据结构(又名“半边数据结构”)由美国Stanford大学的B. G. Baumgar t提出,用于存储镶嵌几何模型。对于管理镶嵌格发生变化的模型是很有用的,如在子分或者简化过程中发生变化。
翼边数据结构是计算机图形学中描述多边形网格的一种常用的数据边界表示。它明确地描述了三个或者更多表面相交时的表面、边线以及顶点的几何以及拓扑特性。
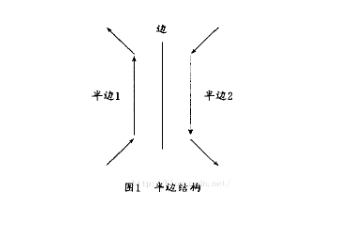
它的基本出发点是以边为核心,每条边上有上下两个顶点,左右两个邻面以及和顶点相连的四条边,这些边分别在两个邻面的边构成的环上。这样就可以建立起边与顶点、边与边、边与面的关系。这种数据结构可以从一条已知边出发,有规律地找到这个几何体的所有面、边和顶点。翼边结构的特点是数据结构有固定数目和长度的数据域。
优点
优点是可以方便、快速地获得以下信息:
- 哪些面使用了这个顶点
- 哪些边使用了这个顶点
- 哪些面使用了这条边
- 哪些边构成了这个面
- 哪些面和这个面相邻
解决以上的问题后,可以方便得创建Shadow Volume。
缺点
缺点是太零散:在查询哪些是多边形以及一个多边形的边数时,无法直接查询,需要通过非得循环找一圈才能得出结果。
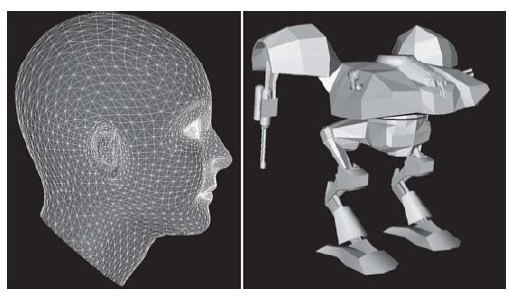
二、三角形网格(Triangle Mesh)
这是最常用的模型之一,例如:当网格在程序中保持不变时等情况。任意多边形网格都能转换成三角网格,三角网格以其简单性而吸引人,相对于一般多边形网格,许多操作对三角网格更容易。实现三角形网格只需要三种特征:顶点、边和三角形。
在翼边结构中,与边相邻的环有两个,由于翼边结构没有明确边的正向,因此要确定当前边所在的环与面较困难,于是人们对翼边结构作了种种改进,其中芬兰赫尔辛基技术大学的Martti Mantyla 教授提出的半边结构( half - edge structure)是其中较有代表性的一种。在半边结构中,将一条边一分为二,其中一条半边属于它一个相邻面的边环,而另一条半边属于它另一个相邻面的边环(如图1所示)。每一条半边仅存储它的起点指针,这样两条半边能够表示一条边的两个端点,当搜索一个面的各端点时,只需沿着半边顺序即可。
三、场景图
场景图(Scene Graph)是一种安排场景内对象的数据结构,它把场景内所有的 节点(Node) 都包含在一个 树(tree) 上。(场景图虽然叫做"图",但实际使用一个树结构来表示)。可以通过中序、先序等方法遍历场景图结构。
参考博客:https://blog.csdn.net/lafengxiaoyu/article/details/51398040
参考博客:https://www.cnblogs.com/yuanjiangw/p/11291675.html
参考链接:https://www.zhihu.com/question/25337780

