深度学习之正向传播、反向传播和计算图——2020.3.1

一、正向传播

（ 一 ） 定义

     正向传播是指对神经⽹络沿着从输⼊层到输出层的顺序，依次计算并存储模型的中间变量（包括输出）。为简单起⻅，假设输⼊是⼀个特征为 \(x \in R^d\) 的样本，且不考虑偏差项，那么中间变量:

\[z = W^{(1)}x \]

其中 $$W^{(1)} \in R^{h \times d}$$是隐藏层的权重参数。把中间变量 \(z \in R^h\) 输⼊按元素运算的激活函数$ \phi$后，将得到向量⻓度为 \(h\)的隐藏层变量:

\[h = \phi \left( z \right) \]

隐藏层变量 \(h\)也是⼀个中间变量。假设输出层参数只有权重 \(W^{(2)} \in R^{q \times h}\) ，可以得到向量⻓度为 \(q\) 的输出层变量

\[o = W^{(2)}h \]

假设损失函数为 \(l\)，且样本标签为 \(y\)，可以计算出单个数据样本的损失项

\[L = l(o,y) \]

根据 \(L_2\)范数正则化的定义，给定超参数 \(\lambda\)，正则化项即

\[s=\frac{\lambda}{2} \left( ||W^{(1)}||^2_F + ||W^{(2)}_F|| \right) \]

其中矩阵的Frobenius范数等价于将矩阵变平为向量后计算 \(L_2\) 范数。最终，模型在给定的数据样本上带正则化的损失为:

\[J = L+s \]

将 \(J\) 称为有关给定数据样本的⽬标函数。

（ 二 ）正向传播的计算图

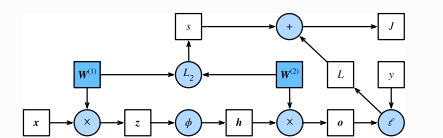
     可通过绘制计算图来可视化运算符和变量在计算中的依赖关系。例如前节softmax回归实现中，绘制的样例模型正向传播的计算图，其中左下⻆是输⼊，右上⻆是输出。可以看到，图中箭头⽅向⼤多是向右和向上，其中⽅框代表变量，圆圈代表运算符，箭头表示从输⼊到输出之间的依赖关系。

二、反向传播

     反向传播指的是计算神经⽹络参数梯度的⽅法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输⼊层的顺序，依次计算并存储⽬标函数有关神经⽹络各层的中间变量以及参数的梯度。
     关于反向传播的计算，主要会用到链式法则。