Lecture06_光栅化 2(反走样和帧缓冲,即Antialiasing and Z-Buffering)_GAMES101 课堂笔记——2020.2.28
内容概览:

一、为什么需要使用反走样?
因为如左图所示是我们需要采样的三角形,右图是根据判断像素点是否在三角形内,采样后进行填充后的图案。明显看出右图和左图的差异性,这种现象叫做“锯齿”,我们改善这种现象,可通过“反走样(或者抗锯齿 )”改善。

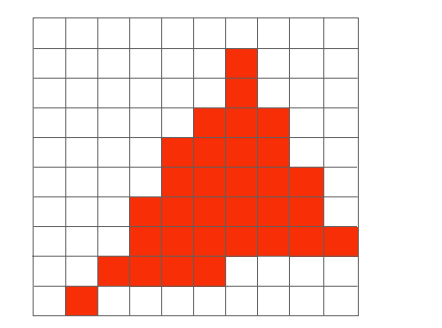
二、图形学中的采样
采样在图形学中无处不在。常见的采样有:
- Rasterization = Sample 2D Positions
- Photograph = Sample Image Sensor Plane
- Video = Sample Time
三、图形学中的采样瑕疵
( 一 )典型的采样瑕疵:
- Jaggies (Staircase Pattern)
- Moiré Patterns in Imaging

- Wagon Wheel Illusion (False Motion)

( 二 )采样瑕疵原因
上述三种采样瑕疵原因就是信号变化太快,采样跟不上信号变化。
三、反走样方法
( 一 )先模糊处理,再进行信号采样。从而达到反走样效果。
采样前进行模糊(预过滤)(Blurring (Pre-Filtering) Before Sampling)

四、频域(Frequency Domain)
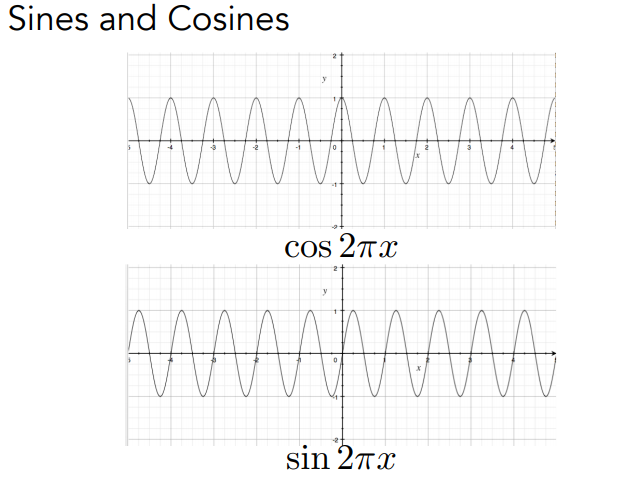
( 一 )傅里叶变换
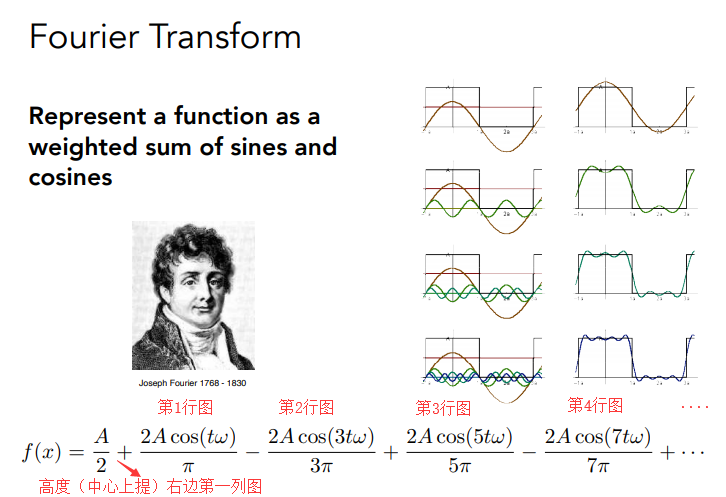
傅里叶变换可以将任何一个函数描述为许多项正弦、余弦函数和。
傅里叶变换应用:
傅立叶变换分解的信号转换成频率:
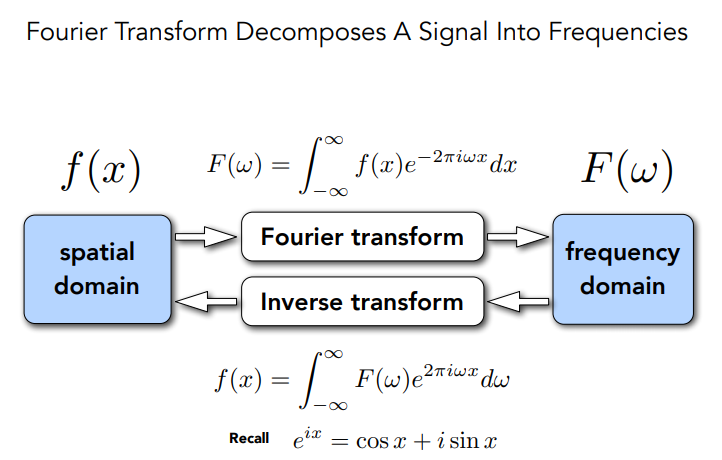
应用:
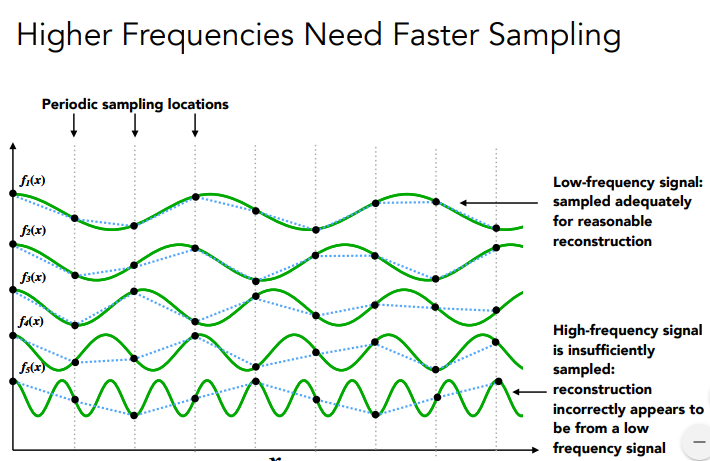
下图绿色曲线是不同的函数,竖直的虚线是采样间隔及位置,黑点是采样点,将采样点连接成采样的函数。
从上至下,函数的频率越高,采样频率相同;但是发现采样结果与原函数采样差别越大,由此造成走样现象。
结论:更高的频率函数需要更快的采样。
( 二 )走样
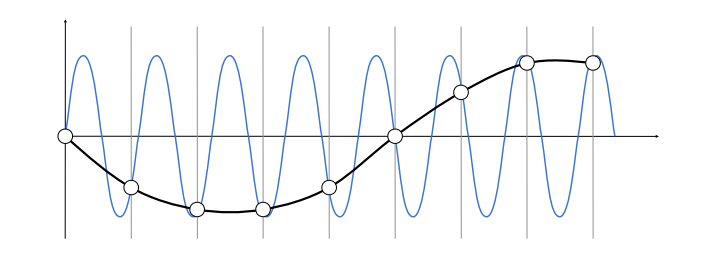
通过频率分析走样,假设:
- 第 1 种情况:蓝色是原函数,进行采样,采样结果是黑色线。
- 第 2 种情况:黑色是原函数 ,对其进行采样,采样结果仍为黑色线。
结论:使用同样的采样方法,采样不同的信号,得到的采样结果可能相同。
五、过滤 = 去掉某些特定频率
-
高通滤波器:只剩下高频信息。(Edges)
可提取出边界信息。“信号变化非常大”==>高频信息

-
低通滤波器: 只剩下低频信息 (Blur)
得到相对模糊的图。

-
过滤高低频信息

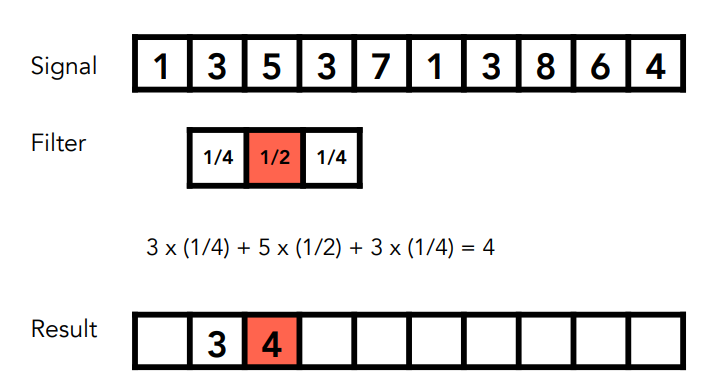
六、过滤 = 卷积(= 平均)
卷积过程释义:
通俗理解为加权平均。
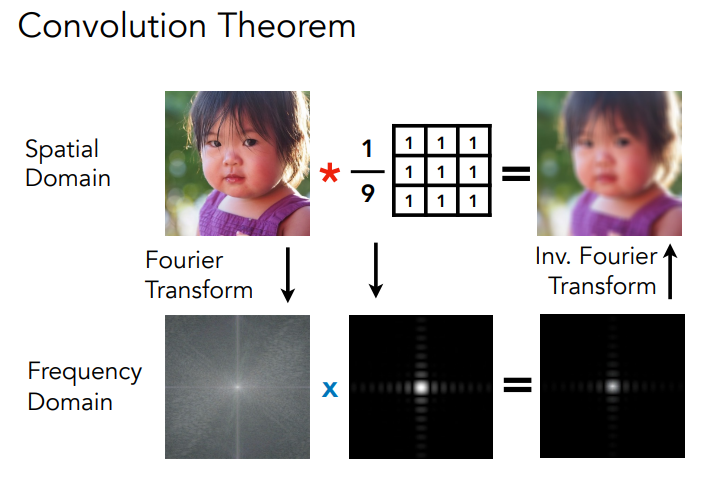
( 一 )卷积定理
Box Fileter:
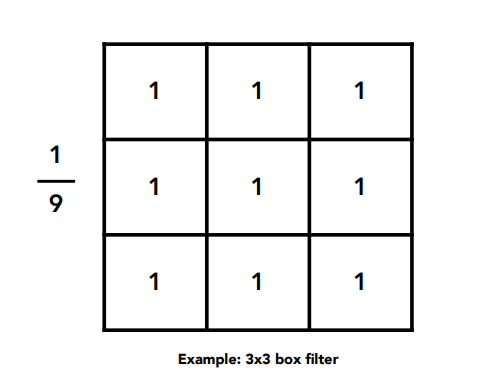
Box Function = "Low Pass" Filter,Box 越大。越模糊;若 Box 越小,甚至 < 像素大小,留下了更大的频域,相当于没有模糊处理。
七、采样 = 重复频率(频域)上的内容


