Lecture05_光栅化 1(三角形)_GAMES101 课堂笔记——2020.2.25
今日学习内容概览:
- Finishing up Viewing
- Viewport transformation
- Rasterization
- Different raster displays
- Rasterizing a triangle
一、透视投影(Perspective Projection)
( 一 )粗略方法:
确定近平面(l,r,b,t),保持远、近平面不的点变,将远平面变为近平面一样大小:
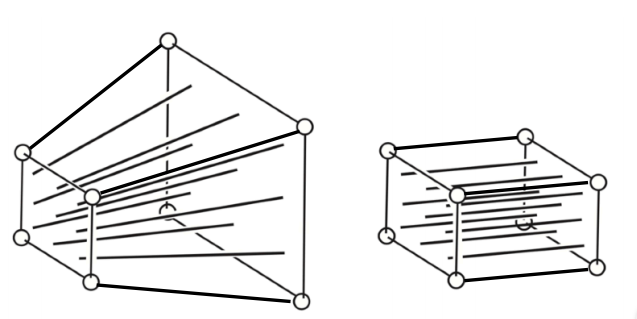
( 二 )细致处理:
有时通过垂直的视角(field-of-view,fovY)和宽高比(aspect ratio = width / height),(假设对称性即L = -r,B = -t).
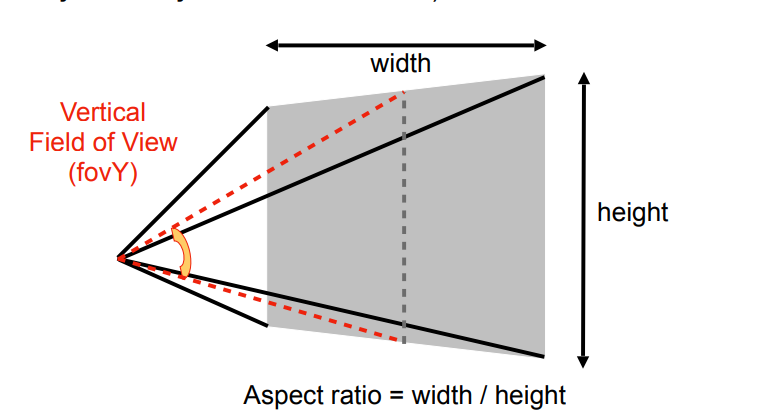
( 三 )转换fovY和面为l,r,b,t
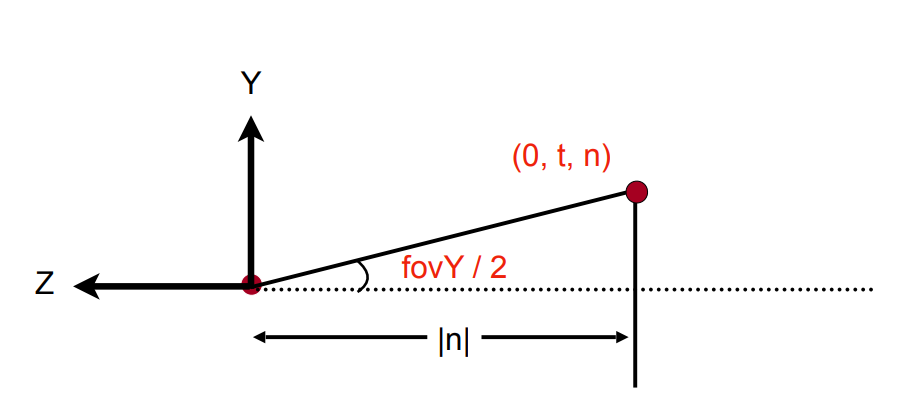
计算公式:
\(\tan \frac{fovY}{2} = \frac{t}{|n|}\) \(aspect = \frac{r}{t}\)
二、规范立方体(Canonical cube)
在 MVP 后,即进行规范立方体到屏幕(画到屏幕)
MYP概念:
- 模型转换(载置对象)
- 查看变换(放置相机)
- 投影变换
- 正投影(长方体到“规范”立方体\(\left[-1,1 \right]^3\))
- 透视投影(平截头体到“规范”的立方体)
( 一 )屏幕的定义:
- 像素的组合
- 数组大小即为——分辨率 eg:1920*1080
- 典型的光栅成像设备
( 二 )光栅化和屏幕的关系:
- Raster == screen in Germa
- Rasterize == drawing onto the screen
( 三 )像素(Pixel)
- 可通俗理解为:一个像素就是一个颜色的小正方形
- 颜色是由 RGB 组合而成
( 四 ) 屏幕空间定义:
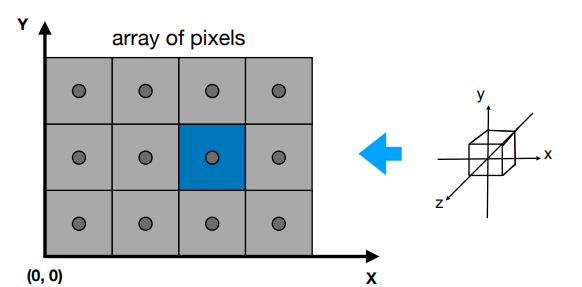
像素的排列:
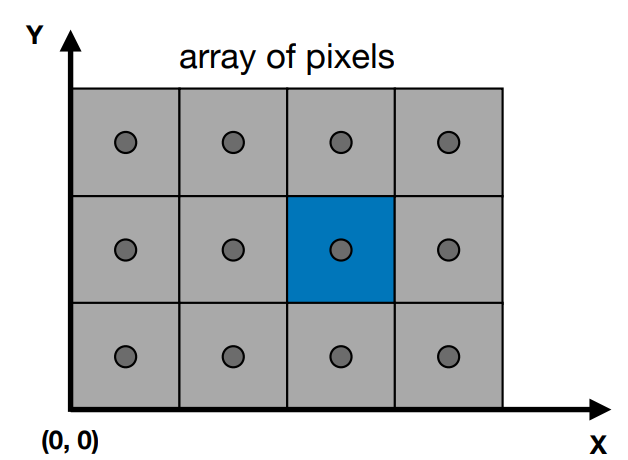
-
约定:
- 像素坐标为(x,y)形式,并且x,y为整数(相当于个数)
- 像素坐标范围:(0,0)到(宽度-1,高度-1)
- 像素(x,y)的中心点是(x+0.5,y+0.5)
- 屏幕占比范围(0,0)到(宽度,高度)
-
与z无关
-
Transform in xy plane: [-1, 1]2 to [0, width] x [0, height]
-
Viewport transform matrix:
三、显示设备
( 一 )数控记号笔拉丝机

( 二 )激光切割机

( 三 )不同的光栅显示器
-
示波器

-
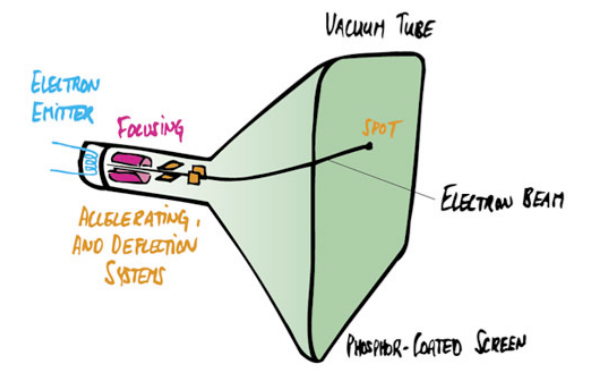
阴极射线管
-
电视 - 光栅显示(CRT 显示器的应用)
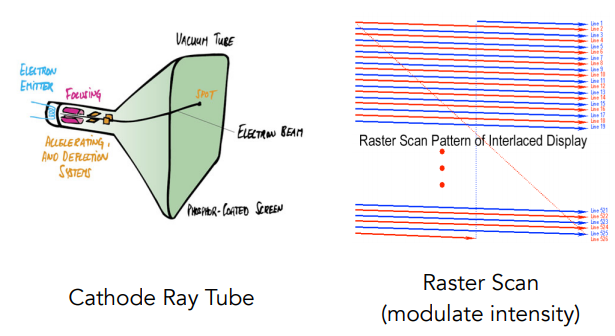
右边的图像是隔行扫描技术(eg:将画面分为两部分,上半部分扫描奇数行,下半部分扫描偶数行),目前在一些视频压缩中仍有应用。缺点:容易造成画面撕裂,尤其是高速运动(eg:体育运动出现鬼影)
- 帧缓存:内存为光栅显示
显存,也被叫做帧缓存,它的作用是用来存储显卡芯片处理过或者即将提取的渲染数据。如同计算机的内存一样,显存是用来存储要处理的图形信息的部件。
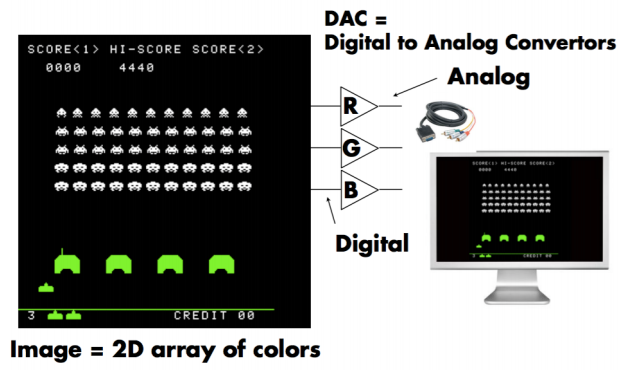
DAC——数模转换器,又称D/A转换器,简称DAC,它是把数字量转变成模拟的器件。D/A转换器基本上由4个部分组成,即权电阻网络、运算放大器、基准电源和模拟开关。模数转换器中一般都要用到数模转换器,模数转换器即A/D转换器,简称ADC,它是把连续的模拟信号转变为离散的数字信号的器件。
- 平板显示器

视网膜显示器:分辨率已经大于人肉眼的分辨率屏幕。
LCD工作原理示意如下:
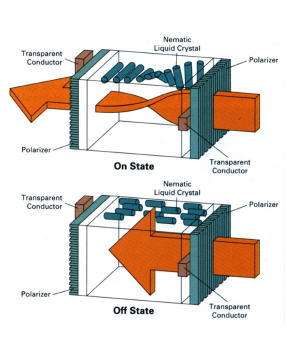
LCD——液晶显示器,通过液晶将竖直的光扭转为水平的光。
- Electrophoretic (Electronic Ink) Display
例如:kindle,通过黑白墨水,控制电子号,从而进行显示。缺点:因为改变黑白朝向耗时,因此刷新率低。

三、光栅化:绘图到光栅显示
( 一 )网格
-
多边形网格(Polygon Meshes)

-
三角形网格(Traingle Meshes)


( 二 )三角形 - 基本形状图元
-
Why triangles?
- 最基础的多边形
- 可由别的多边形拆解而来
- 独特的性质
- 保证是平面
- 能够定义良好的内部
- 定义方法:可通过定义三角形的三个点,实现渐变效果
- 最基础的多边形
-
什么像素值近似三角形?

判断一个像素(中心点)与三角形的位置关系===>通过采样实现。
采样:给一个连续函数得到值,即一个函数的离散化过程。
四、采样
在评估一个点的函数取样。我们可以通过采样离散函数。如下:
for (int x = 0; x < xmax; ++x)
output [x] = f(x)
采样是图形学的核心理念,可以采样的:时间(1D)、面积(2D)、方向(2D)、体积(3D)等等
( 一 )光栅化作为2D采样

例如:如果每个像素的中心是三角形内
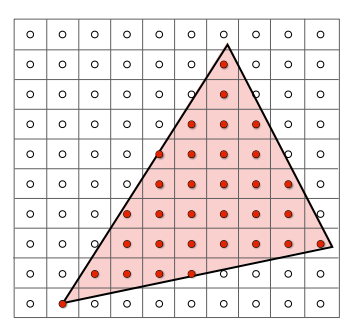

定义二元函数:\(inside(tri, x, y)\)(注:X,Y:不必为整数)

光栅化=采样A 2D指示灯功能
for (int x = 0; x < xmax; ++x)
for (int y = 0; y < ymax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);
这个循环函数让像素中心值为 0 或 1 (0表示不在三角形内部,1表示在三角形内部),根据中心点为的值从而给予某种颜色。
( 二 )回顾:样本位置

( 三 )回顾:叉乘
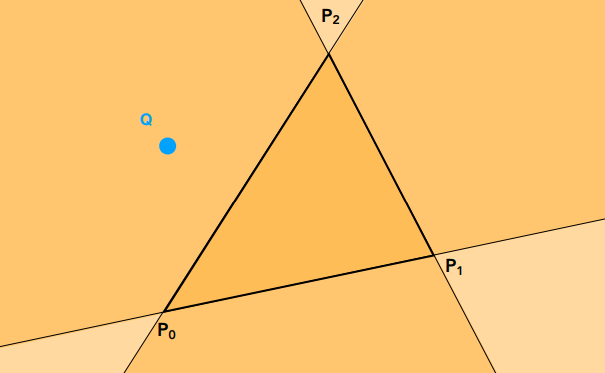
通过某一点(例如:Q点)与三角形\(P_{0}P_{1}P_{2}\)的边长位置关系做判断。规定某一个方向,以逆时针方向举例,\(P_{2}P_{1} \times P_{2} \times Q\)得知,叉乘指向朝上,因此Q点在\(P_{2}P_{1}\)的右边;同理可得,Q 点在\(P_{1}P_{0}\)的右边,但 Q 点在\(P_{0}P_{2}\)的左边。(点位于三条边的方向并不完全一致)**====》因此,Q点在三角形\(P_{0}P_{1}P_{2}\)的外部。
如果是在像素中心点在边界呢?
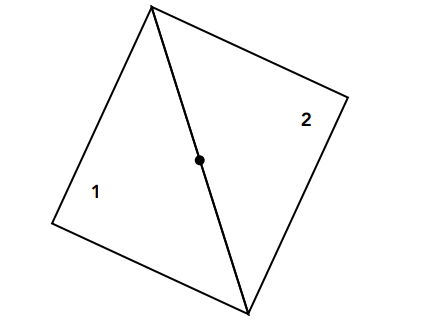
两种方法:一种是不做处理(本堂课采用),另外是做特殊处理。
注:图形学的第三方库API如OpenGL和DirectX对边界点有严格的规定。即中心点在三角形的上边/左边,则算作在三角形内部;若点在三角形的下边/右边,则不属于三角形内部。
检测屏幕中所有的像素
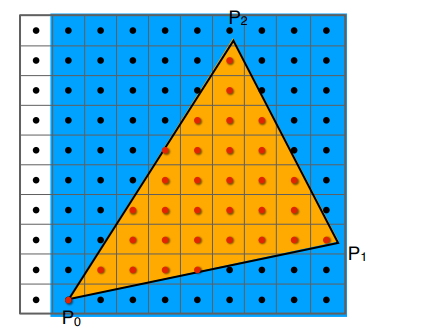
检测像素的步骤:
1. 首先通过 x,y 的坐标从最小值到最大值选出包围盒(Bounding Box)。(即蓝色包围部分,去掉第一列白色部分。此通过水平和竖直确定的包围盒,还可称为**轴向包围盒=AABB包围盒(Axis-aligned bounding box))**
2. 在区域内进行循环,使用inside函数确定像素中心点的值。
AABB是应用最早的包围盒。它被定义为包含该对象,且边平行于坐标轴的最小六面体。故描述一个AABB,仅需六个标量。AABB构造比较简单,存储空间小,但紧密性差,尤其对不规则几何形体,冗余空间很大,当对象旋转时,无法对其进行相应的旋转。处理对象是刚性并且是凸的,不适合包含软体变形的复杂的虚拟环境情况。
AABB也是比较简单的一类包围盒。但对于沿斜对角方向放置的瘦长形对象,其紧密性较差。由于AABB相交测试的简单性及较好的紧密性,因此得到了广泛的应用,还可以用于软体对象的碰撞检测。
光栅化加速方法之——增量三角形遍历
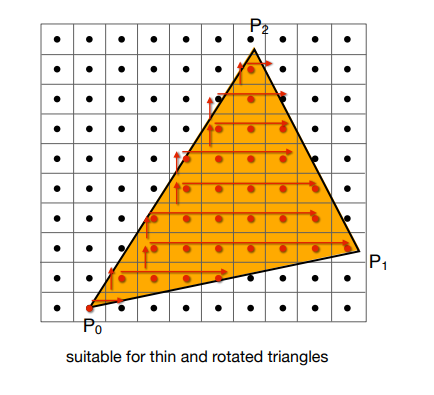
这种方法是在每一行的从最左到最右,确定一个包围盒。适用于窄长、旋转的三角形(即实际在AABB盒中覆盖了很少的像素。)
( 四 )实际屏幕中的光栅化
- 下面是两个手机屏幕的光栅化图像:

- iPhone :每个像素由3条(RGB)代表一个像素
- Galaxy :使用\(Bayer Pattern\)方法,使RGB均匀分布。现象:其中绿色点最多(观察方法:只看某一种颜色,分别看三种颜色点,即可看出。)这是因为人眼对绿色更敏感,这样看起来跟舒服。
- 彩色打印

如果加的颜色越多,那么会更黑;RGB值越高,图片越亮。
( 五 )按照像素为一个正方形(本课程采用),展示一个示例:
-
采样信号展示:

-
The Display Physically Emits This Signal(进行填充后为左图,实际图形为右图)
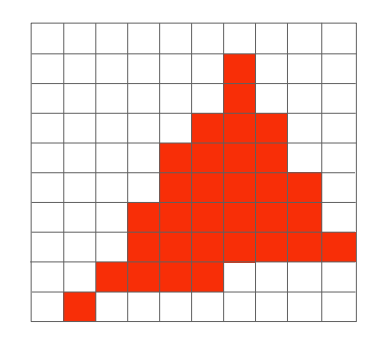

由此,发现一个问题,采样填充后的图像并不完全符合原始图像,出现锯齿(Jaggies)现象。同样的现象见下图:

原因: 因为像素本身具有大小,采样率不高,从而信号走样(Aliasing)。
目前,仍是图形学一直不断改进的问题,下节课将介绍如何解决“锯齿”问题,引入抗锯齿和反走样的概念。

