Lecture04_转换控制_GAMES101 课堂笔记——2020.2.21

学习内容概览：

• 3D transformations
• Viewing（观测）转换
  • View/Camera transformation
  • Projection（投影） transformation
    • Orthographic(正交) projection
    • Perspective(透视) projection

上节内容补充：

     旋转 \(\theta\) 角是旋转 \(-\theta\) 角的矩阵转置，如果旋转 \(R_{\theta}^T = R_{\theta}^{-1}\),则该矩阵为正交矩阵。

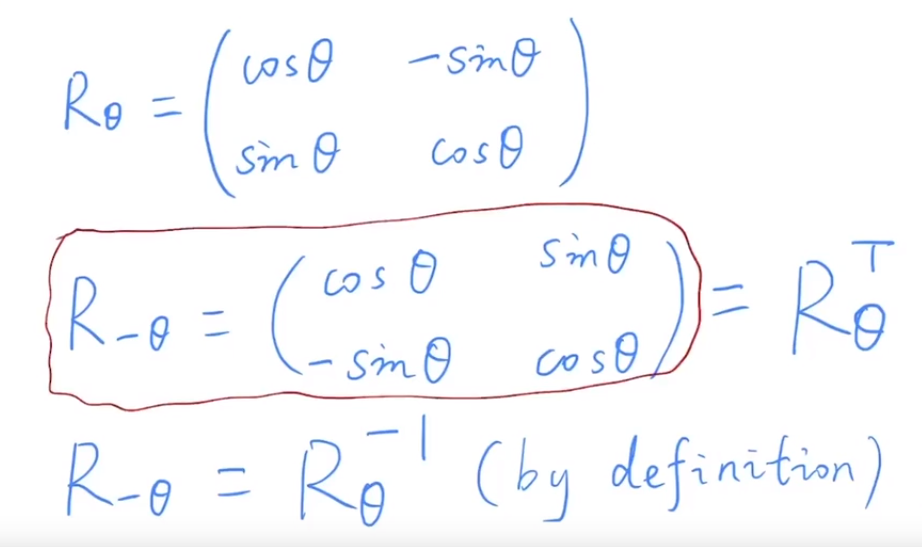
一、3D transformations

    类似2D使用齐次坐标表示(点用1，向量用0)：

• 3D point = \(\left(x,y,z,1\right)^T\)
• 3D vector = \(\left(x,y,z,0 \right)^T\)
      通常，\((x,y,z,w)(w!=0)\)是3D的点：

\[\begin{pmatrix} x^{'} \\ y^{'} \\ z^{'} \\ 1 \end{pmatrix} = \begin{pmatrix} a & b&c&t_x \\ d& e&f&t_y \\ g&h&i&t_z \\ 0&0&0&1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \]

( 一 )齐次坐标表示3D 变换

顺序：先线性变换再平移。

1. 3D 变换

• 缩放和平移：
  

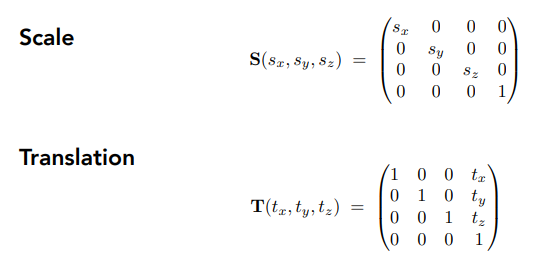
• 绕着x、y、z轴旋转：
      固定旋转轴，分别绕着另外两个轴旋转。
  问题：为何绕 Y 轴旋转的旋转矩阵中 \(-\sin \alpha\) 与 \(\sin \alpha\) 的位置不同?
  Ans：因为 \(X \times Y\)得到 \(Z\) 轴， \(Y \times Z\)得到 \(X\) 轴，连续书写字母顺序是：XYZXYZ...但是\(Z \times X\)得到 \(Y\) 轴，所以 \(Y\) 因此是反的。
  

2. 3D 旋转

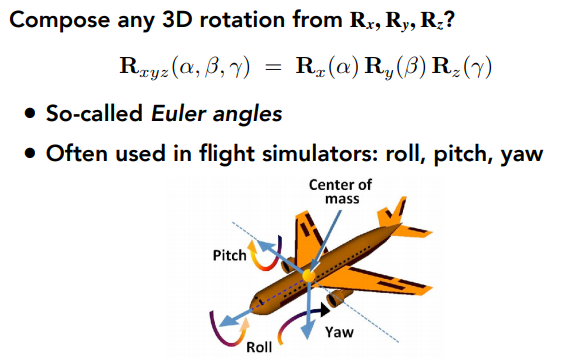
    对于任意一个旋转 \(R_{xyz} \left(\alpha,\beta,\gamma\right)\),可以由 \(R_x\left(\alpha\right)\) 、\(R_y\left(\beta\right)\) 和 \(R_z\left(\gamma\right)\) 组成。其中，\(\alpha\) 、\(\beta\) 和 \(\gamma\) 称为欧拉角（Euler Angles）。通过下图中的操作，可将飞机的头朝向任意方向。

3. 罗德里格斯公式（Rodrigues’ Rotation Formula）

      在三维旋转理论中，对于给定旋转轴和旋转角度，以Olinde Rodrigues命名的罗德里格斯公式是用于在空间旋转向量的高效算法。
     旋转轴为 n 轴，旋转角为 \(\alpha\) .默认旋转轴过原点(若不过原点，可想将其移至原点，然后做线性变换后，在将其平移至原位置）。其中，罗德里格斯公式如下：

另外提到一个概念：

四元数：便于计算旋转与旋转之间的差值。

二、观测变换（View/Camera Transformation）

（ 一 ）What is view transformation?

     以上三步简称"MVP"变换。

（ 二 ）How to perform view transformation?

1. 主要定义三个要素：

• 位置
• 观测方向
• 向上的方向（类似地图上的向北指向，以便确定整个观测的位置。）
  

2. 进行视图变换

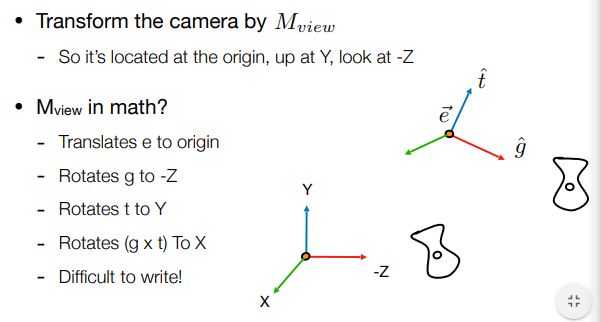
     约定：相机在原点，向上指向 Y，看向 Z 方向。

3. 相机转换步骤

4. 写成转换矩阵

总结

三、投影变换

（ 一 ）投影变换的分类

     其中，人眼成像类似于透视投影（右图）；正交投影（左图）常用于工程制图。

（ 二 ）透视投影 VS 正交投影

     透视投影是在一个点投射成四棱锥形成；正交显示若将相机放于无限远，远、近平面将无限接近。

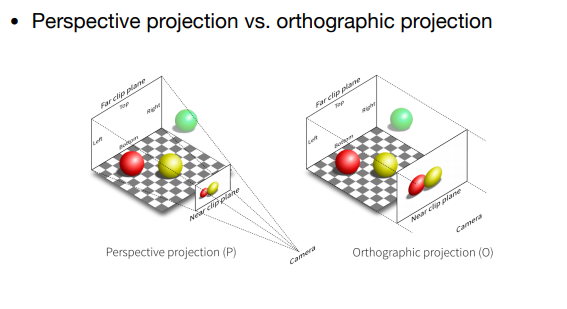
下面，将对透视投影和正交投影分别进行阐述。

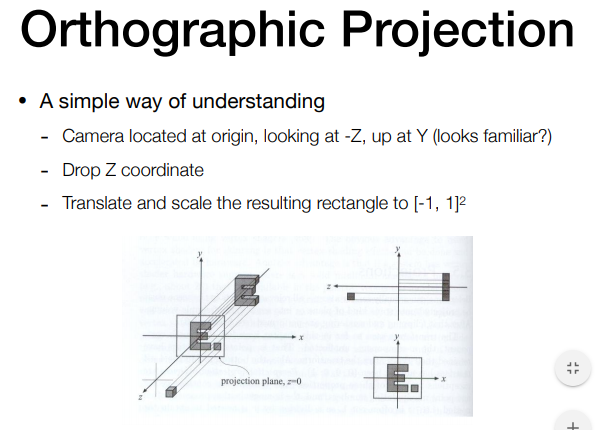
四、正交投影

（ 一 ）3D化2D方法：

     主要将平移和缩放放在\(\left[-1,1\right]^2\)中。

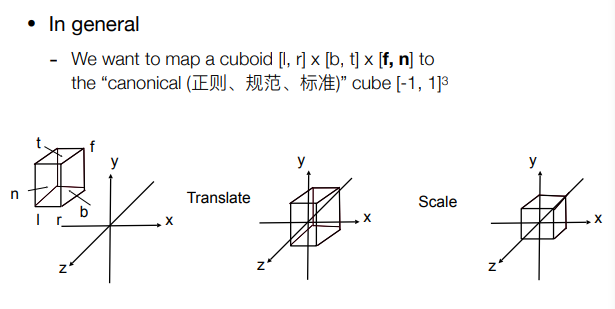
（ 二 ）3D 常用方法

     定义一个空间中的立方体，将其映射成标准立方体\(\left[-1,1\right]^3\)中。“先平移再缩放”。

注意：此时的\([f,n]\)中，远平面 f < 近平面 n,因为是沿着 \(-Z\) 方向查看。但是在OpenGL中，由于是左手坐标系，因此f>n,是 \(\left[n,f\right]\) 。

     变换步骤：先平移再缩放。

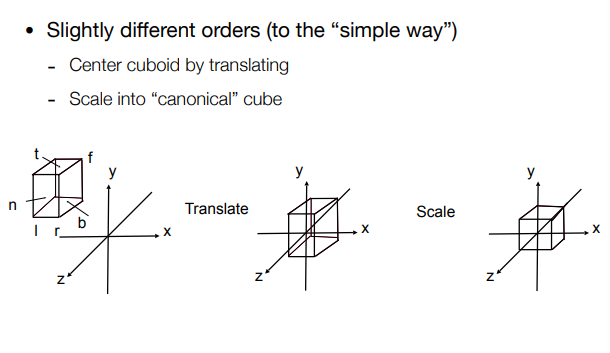
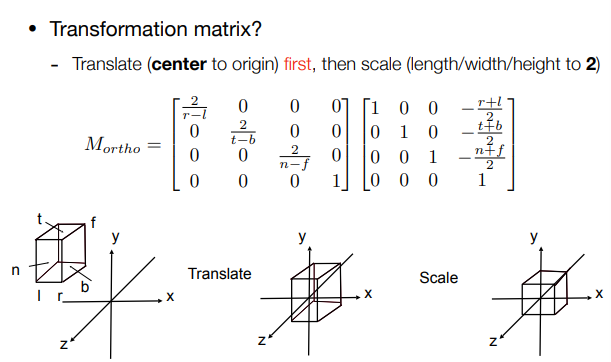
（ 三 ）变换矩阵

     先将中心移至原点，再将其边长缩放为2。（在坐标轴[-1,1]范围内。）

     坐标系选择不同，会导致结果不同。

五、透视投影

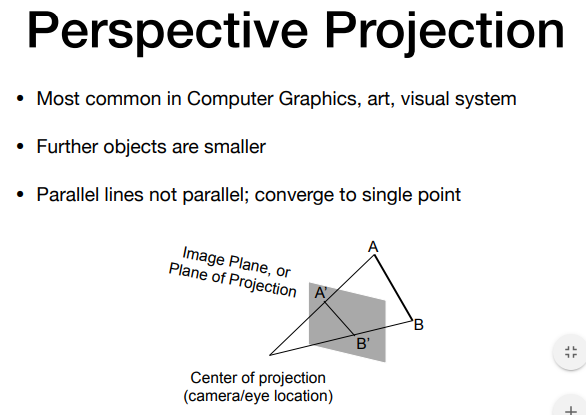
     透视投影是目前最广泛的投影，近大远小，效果：放远处平行线不再平行，例如这个平行的铁轨。

     其中关于那个矛盾，是因为欧式几何是在同一个平面内，而这个铁轨照片里面包含了许多个平面，是在不同平面、不同角度，因此会感觉有些矛盾。

（ 一 ）回顾：齐次坐标性质

     其中，这里面这个结论很重要，在后面进行透视投影中会用到。

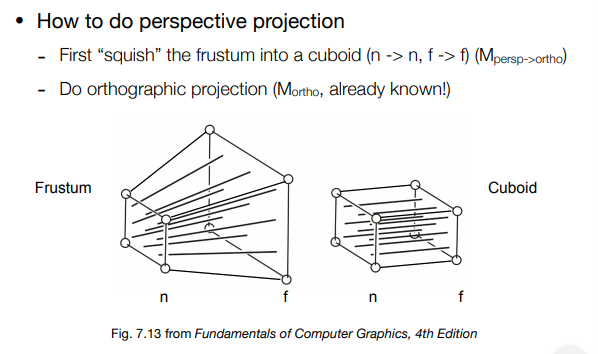
（ 二 ）怎样进行透视投影？（难点）

     简单说，就是把这个Frustum的远平面f挤成同近平面n一样大的平面，然后进行正交投影。
约定：

• 近平面不变
• 远平面f的中心点不变
• Z值仍为f
  
       关于远平面挤压后坐标的变化,（通过相似三角形算出）等值关系：
  
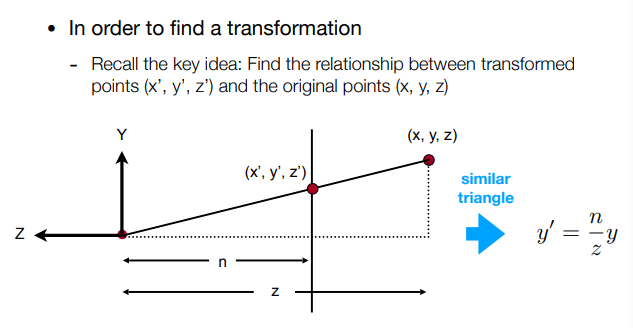
       在齐次坐标中，利用乘以一个数，仍为原点，先乘以 \(\frac{n}{z}\)。
  
       透视投影到正交投影：
  
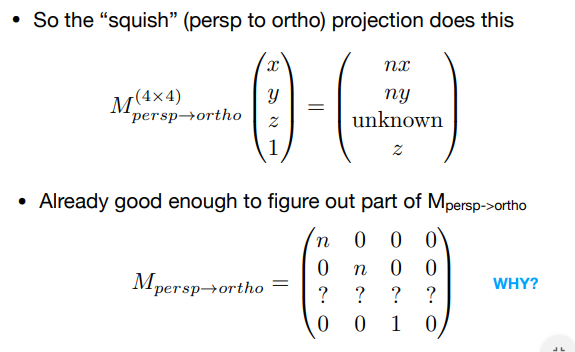
       求第三行四个问号的值：

1. 观察特殊性——远、近平面的点特殊性：

2. 利用近平面的点不变性，计算出第三行的前两个问号，得出一个等式\(An + B = n^2\)：

3. 利用远平面的点，Z坐标值不变性，得出\(Af + B = f^2\)：

     

4.将第2、3步的等式联立，得出A、B的值。

Question：对于中间任意一点（x,y,z），在经过挤压后（将其变为立方体后），变换后的Z值会靠近远平面还是靠近近平面？
Ans：会更大一些，因为是双曲线上的一段。