激活函数总结——2020.2.10

一、激活函数简介

    首先，我们先通过三个问题掌握神经网络激活函数的概念及意义：
1. 为什么需要激活函数？
    神经网络可以看成是一个多层复合函数，早期引入激活函数就是为了使其具有非线性，因为引入之前为线性函数相互复合，但这样得到的最终结果仍旧是线性的。假如需要将一个 n 维向量，变成 m 维的向量（即：\(R^n \rightarrow R^m\)），则需要利用激活函数的非线性来达到目的。

2. 什么函数可用作激活函数？
    激活函数必为非线性函数，另外激活函数在神经元数足够的情况下，应尽可能使神经网络可以实现对任何一个输入向量到输出向量的连续映射函数逼近，即：万能逼近定理（universal approximation theorrm）。

万能逼近定理：
    优点：用一个简单到不能再简单的函数的线性组合和叠合可以逼近任何连续函数。
    缺点：天下没有免费的午餐。
    举例：

• 一维阶梯函数的线性组合能逼近任何连续一维连续函数。
• Sigmoidal 函数可以逼近阶梯函数。因此,一维Sigmoidal函数的线性组合能逼近任何连续函数。

3. 如何评价激活函数的好坏？
    首先，我们需要了解梯度消失、梯度爆炸两个概念。其中，好的激活函数就需要尽可能避免这两种现象。
梯度消失
    反向传播算法在计算误差时每一层都会乘以本层激活函数的导数。如果本层激活函数的导数绝对值小于1，那么多次连乘后会导致误差项逐渐接近于0，由于参数的梯度值由误差值计算所得，因此会导致前几层的权重梯度接近于0，这样参数并不会得到更新。因此，该现象被称为梯度消失问题

梯度爆炸
    梯度爆炸可以看做与梯度消失相反，即激活函数的导数绝对值大于1，多次连乘后的误差项会趋于一个非常大的数，由此造成梯度爆炸。

二、激活函数汇总

    下图是一些常见的激活函数及其导数，后文将对其概念及应用场景进行大致介绍。
![]

(一)sigmod函数

\[f(x) = \frac{1}{1+exp^{(-x)}} \]

    sigmod函数图像：

    sigmod函数能够将输入的连续实值规范到0~1之间输出。特别地，如果输入的数非常大的负数，那么输出为0；如果输出是非常大的正数，那么输出为1。
sigmod缺点

1. 在深度神经网络中，容易导致梯度消失。
2. sigmod的输出不是zero-centered（0均值），会导致后一层的神经元得到上一层输出的非0值信号作为输入值，可能同时导致收敛缓慢。
3. 计算过程含幂运算，求解耗时。

(二)tanh函数

\[tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \]

    tanh函数图像：

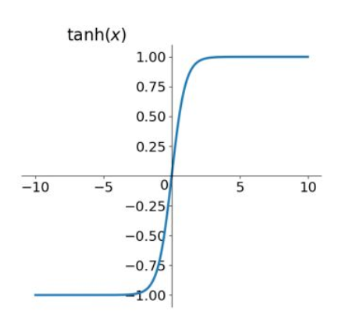
tanh读作Hyperbolic Tangent，可以看做是sigmod的改进，解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

(二)ReLu函数

\[Relu = max(0,x) \]

    ReLu函数图像：

ReLu函数优点

1. 解决了梯度消失的问题，所有的值均≥0.
2. 计算速度快，仅需与0比较，取max即可。
3. 收敛速度比sigmod和tanh更快。

ReLu函数注意事项
    目前ReLu 函数作为常用的激活函数，在参数初始化和设置学习率时需要注意，否则容易造成Dead ReLu Problem（即一些神经元永远不会被激活，导致相应的参数永远不会被更新。）
    解决办法：

• 采用Xavier进行初始化
• 学习率从小开始设置，避免设置太大；或者也可使用adagrad自动调节学习率。

参考博客：https://zhuanlan.zhihu.com/p/40903328
参考博客：https://blog.csdn.net/tyhj_sf/article/details/79932893