【动画笔记】辗转相除法——求最大公约数和最小公倍数

最近咱摸起了C语言，尝试着结合最近学的运筹学写个计算工具，途中遇到了一个需求：分数的约分。

• 分数约分怎样一步到位呢？答案便是找分母和分子的最大公约数。

• 那么怎么尽快算出最大公约数呢？网上查了一查，发现了一个算法：辗转相除法。

这篇笔记就简单而直观地记录一下这个算法。

最大公约数

这个词非常贴近分数中约分的方法，所谓最大公约数即是多个整数共有的约数中最大的一个，在约分的时候分子和分母同时除以最大公约数，能得到最简分数。

因为上面说的过程中进行的都是整除运算，所以最大公约数也称为最大公因数。

不妨说得更直接一点，公因数就是公约数。

---

关于最大公约数的定义有两点需要注意：

1. 公因数/公约数是针对整数而言的。

2. 一般规定最大公约数为正整数，也就是满足如下公式：

   \[\color{Gray} \gcd(a,b) = \gcd(\left | a \right |,b) = \gcd (a,\left | b \right | ) = \gcd (\left | a \right | ,\left | b \right | ) \]

   要算带有负号的数值时，可以给其套上绝对值，再计算。

手算

现实中在求多个整数的最大公约数时，可以把这些数的因数都列举出来找共有的因数，亦或可以使用短除法：

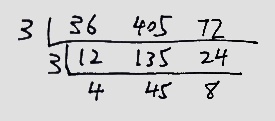
我觉得这些方法其实多少有些依赖我们以往的经验，比如看到36,405,72中有6,5,2，可能很快能想到公因数3。（感觉我大脑里此时枚举了所有可能的因数）

这个过程如果抽象成编程语言中的算法，具体以代码实现，大概就是一个循环+判断所有数除以因数是否余数都为0了，时间复杂度是O(n)，随着运算数值的增大，代码的执行次数也会线性增加。

为了优化时间复杂度，这个时候就到了这篇笔记的主角——辗转相除法了。

辗转相除法

上面提到了求多个整数的最大公约数，在这之前得先看看针对两个整数的二元算法👇

公式

辗转相除法也被称为欧几里得算法(Euclidean Algorithm)，怎么“辗转”的呢？先上公式看看：

\[\color{Gray} \gcd(A,B) = \gcd (B,A \bmod B) \]

A 代表被除数(Dividend)；
B 代表除数(Divisor)；
A mod B 代表 A 取模 B，也就是A除以B后的余数，在C语言里的表达式可以写成A % B。

这里的gcd代表的是Greatest Common Divisor，也就是最大公约数。此公式的含义是：

• [被除数] 和 [除数] 的最大公约数 = [除数] 和 [余数] 的最大公约数

这便是整个“辗转”过程的核心，具体证明这里就不多赘述，可以看看文末的相关文章。

---

辗转

下面演示一下这个“辗转”过程，计算一下36和405的最大公因数：

所谓的辗转实际上指的是一个迭代运算的过程，迭代运算在编程语言里的体现其实就是重复执行一段代码，在每一次执行过程中以上一次执行运算的结果值为基础，运算出新值后代入下一次运算，不断用旧值推算新值，直至达到终止条件为止。

辗转相除法过程的抽象描述如下：

1. 初始化：两个整数之中的较大值A作为被除数，较小值B作为除数。

2. 运算：对 A 和 B 进行 取模（取余数）运算，得到余数C。

3. 迭代：将原本的除数B作为被除数，余数C作为除数，重复第2步的运算。

4. 迭代终止：当某次运算中余数为0时，无法继续进行运算，算法结束，最后一次运算的除数就是最初两个整数的最大公约数。

直观化理解

刚开始我想了好一会儿也没想到这种辗转相除怎么理解，直到查了资料才了解到了古人的智慧方法——几何化表达。

可以这样想，两个整数其实可以看作两个维度，可以在一个二维空间中用一个图形表达出来。显而易见，最适合的图形便是长方形了，长方形对边相等，拥有长和宽两个参数，正好对应了两个整数。

那么除的过程呢？实际上在长方形的长和宽都是整数的情况下（长宽比为有理数），是肯定能被有限个正方形填充满的。除的过程实际上就是往长方形中塞入尽可能大的正方形。

---

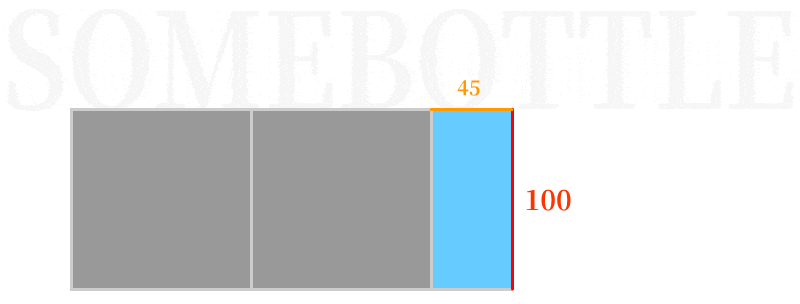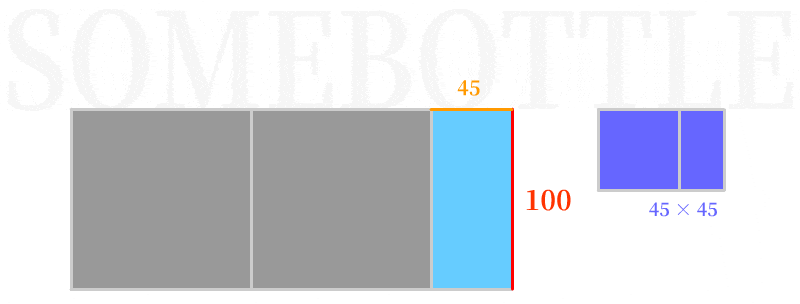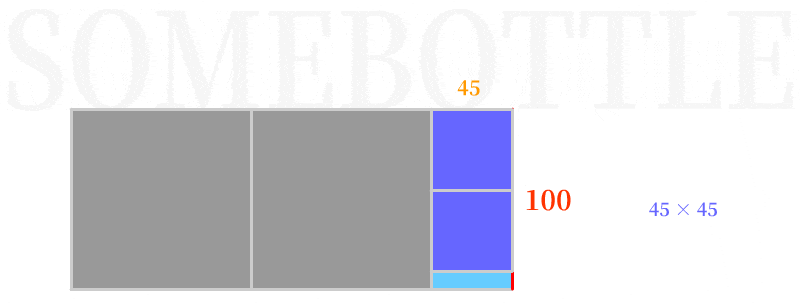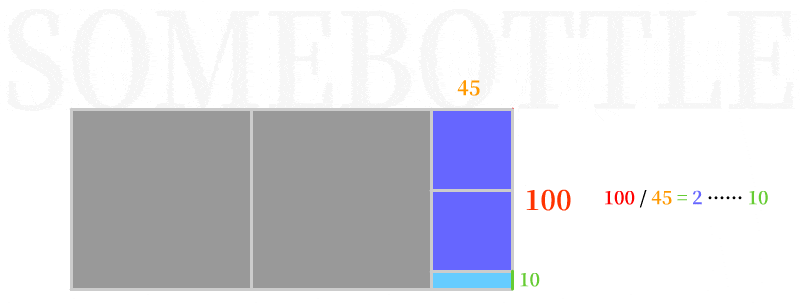
下面直观展示一下辗转相除法求100和245的最大公约数：

👆 首次运算，以短边100为长构造正方形填入（尽可能大的正方形），可见剩余下来的长方形长宽比为100:45，正好对应了下一次运算的被除数和除数。

👆 第一次迭代，以短边45为边长构造正方形填入，剩余下来长方形区域为45:10，对应下一次迭代的被除数和除数。

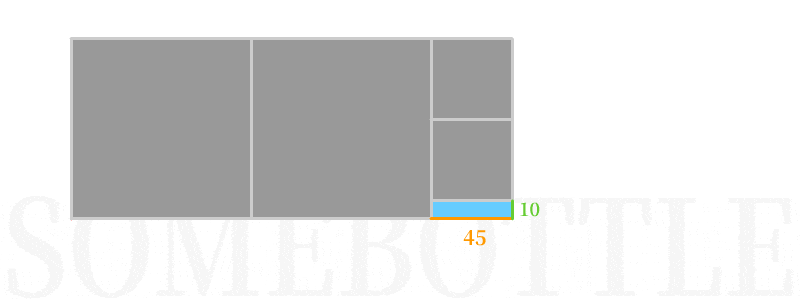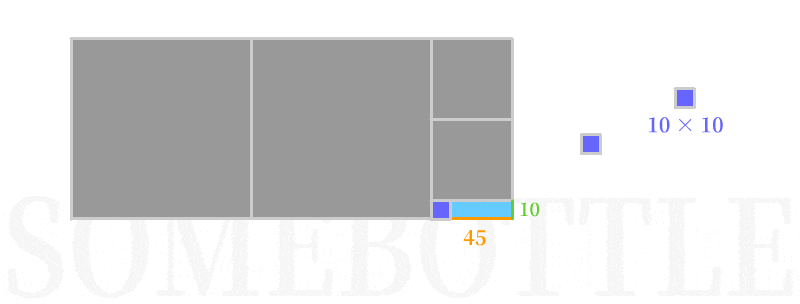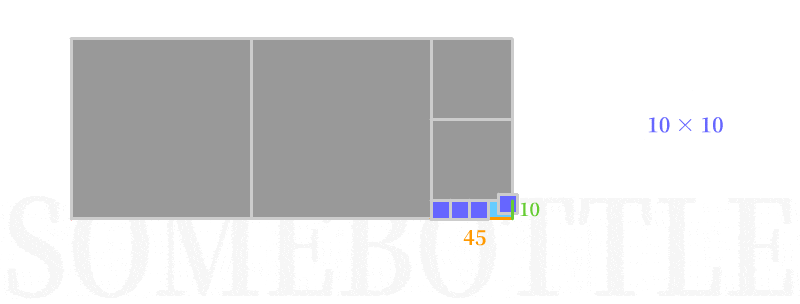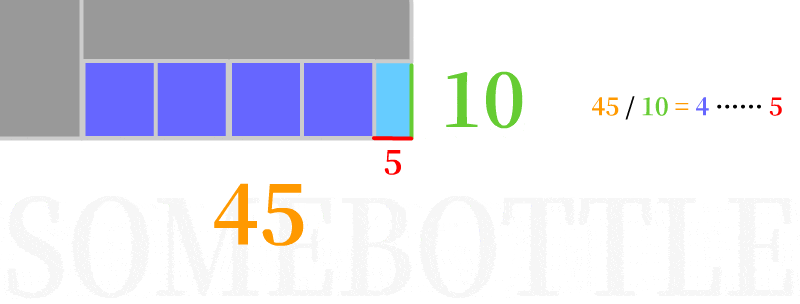
👆 第二次迭代，以短边10为边长构造正方形填入，剩余下来长方形区域为10:5。

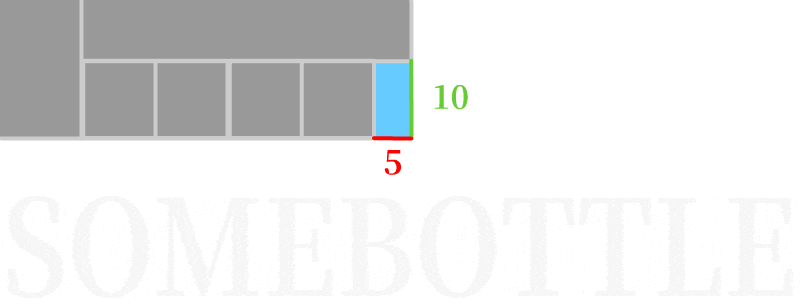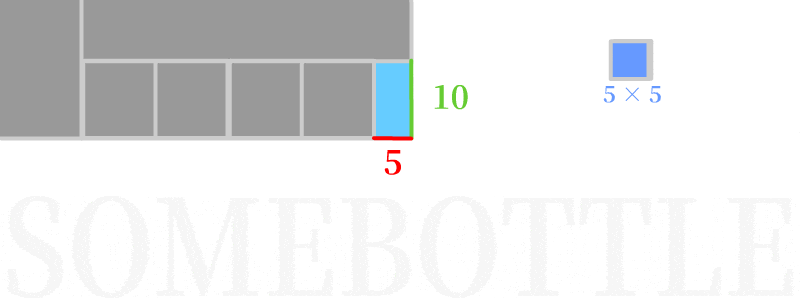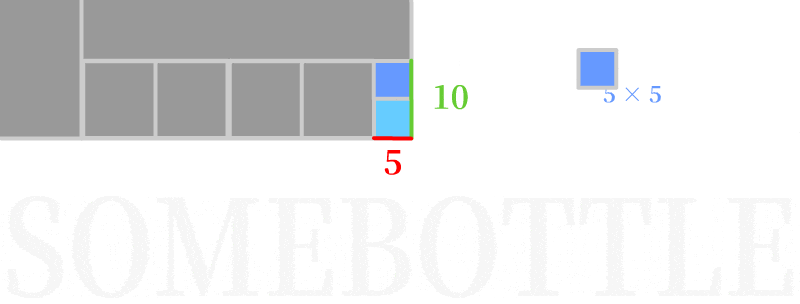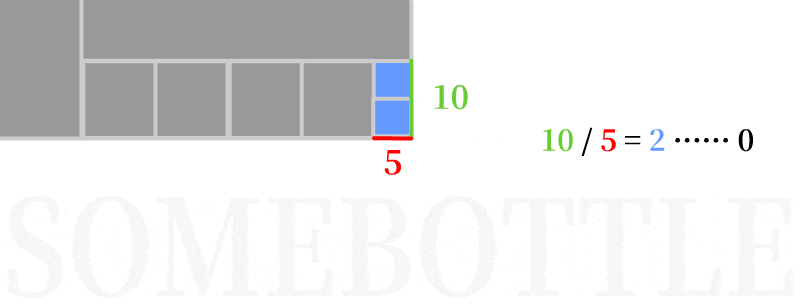
👆 第三次迭代，以短边5为边长构造正方形填入，正好填满了剩余的长方形区域，算法结束，最初两整数的最大公约数为5。

• 即一定数量的5×5的正方形正好能填充满100×245的长方形（正方形的边5正好能整除100和245）。

由此可见，整个算法的过程直观体现出来就是每一次都在剩余的长方形空间中塞入尽可能大的正方形，直至正方形正好能填充满剩余的长方形空间。
（这也是为什么首次运算要用较大的值除以较小的值）

具体实现

这里用C语言实现辗转相除算法：

// #include <math.h>
long int GCD(long int num1, long int num2) {
    // 寻找两数最大公约数(欧几里得算法)
    // 公式 GCD(被除数,除数)=GCD(除数,余数)
    // 这里为了便于理解写的复杂了一些，新定义了三个局部变量
    long int dividend; // 被除数
    long int divisor; // 除数
    long int remainder; // 余数
    num1 = labs(num1); // 给两个数套上绝对值
    num2 = labs(num2);
    if (num1 > num2) { // 较小的数作为除数
        dividend = num1;
        divisor = num2;
    } else {
        dividend = num2;
        divisor = num1;
    }
    do {
        remainder = dividend % divisor;
        dividend = divisor; // 把被除数换成除数
        if (remainder) { // 余数不为0，就把除数换成余数
            divisor = remainder;
        }
    } while (remainder != 0);
    return divisor;
}

时间复杂度

观察发现，该算法的核心操作是“取模”(Modulo)。整个算法可能依赖于多次迭代，每次迭代都会进行取模操作，而每次取模操作后留给下次运算的数据量相对来说都会减少超过一半。

---

为什么是减少超过一半呢？因为每次除法运算中余数的绝对值一定小于被除数绝对值的一半：|余数| < 0.5 |被除数|

下面用文字解释了一下（这张图中所有数都是正整数）：

---

话说回来，提到数据减半，我不由得就想到了二分查找。二分查找每一次迭代只用处理上一次运算中的一半数据，这样下来能推算出其时间复杂度是O(log2(n))级别（我之前尝试着推算过这个）。

回到辗转相除法:

\[\color{Gray} A \bmod B < \frac{A}{2} \]

\[\color{Gray} B \bmod (A \bmod B) < \frac{B}{2} \]

(A是被除数，B是除数)

两次迭代中，A和B的值分别减少了一半，也就是: \(\color{Gray} A + B \to \frac{A}{2} + \frac{B}{2}\)，

对于除数B来说，每次减少一半的时候处于这个区间：1<操作次数<2；因此迭代次数至多为2log(min{A,B})次（这里除数是B，即2log(B)）。

之所以是min{A,B}(取A和B中较小的值)，是因为算法的终止条件是余数为0，也可以理解成除数为0，而算法最开始会选择较小的值作为除数。

所以辗转相除法的时间复杂度是O(logn)级别的。

---

对于两正整数的辗转相除法来说：

• 最好的情况

  首次运算余数即为0，一步完成，时间复杂度为 \(\color{Gray} O(1)\)

• 最糟糕的情况

  一直迭代到除数为 1 （1是所有整数的公因数），余数为0，时间复杂度级别为\(\color{Gray} O(\log_{}{n})\)

求多个整数的最大公约数

辗转相除法是针对两个整数的二元算法。

而如果要求多个整数的最大公约数，只需要化成多次二元辗转相除运算即可。

C语言实现

#include <stdio.h>
#include <math.h>  

// GCD即上述的二元辗转相除函数

long int ArrGCD(long int *arr, int arrLen) {
    long int temp = arr[0];
    int i;
    for (i = 1; i < arrLen; i++)
        temp = GCD(temp, arr[i]); // 用前一次的最大公约数和当前的数进行辗转相除
    return temp;
}

int main() {
    long int testArr[] = {405, 45,180,210};
    int arrLen = sizeof(testArr) / sizeof(int);
    printf("%ld\n", ArrGCD(testArr, arrLen));
    return 0;
}

核心方法：用前一对数值的最大公约数和当前数进行辗转相除，遍历数组进行迭代运算。

时间复杂度

前面针对两个整数的辗转相除的时间复杂度级别是\(\color{Gray} O(\log_{}{n})\)。而在这里需要遍历一次数组元素，且每遍历一个元素需要进行一次辗转相除算法。

一层循环加上对数阶复杂度，很容易能得出这个求多整数最大公约数算法的时间复杂度是：\(\color{Gray} O(n\log_{}{n})\)

求最小公倍数

前面的求最大公约数我是由约分的概念引出的。在分数运算中除了约分，还有一个很重要的运算技巧便是通分。

通分要找的是最小公倍数。

关于最小公倍数

公倍数是两个整数A,B共有的倍数，也就是公倍数可以被A和B整除。

两个整数的公倍数有无限多个，而这些公倍数中除0外最小的一个便是最小公倍数（Least Common Multiple）。

注意：和最大公约数一样，最小公倍数一般规定为正整数。

\[\color{Gray} lcm(a,b) = lcm(\left | a \right |,\left | b \right | ) \]

---

用最大公约数算最小公倍数

在求了最大公约数后，求最小公倍数可谓是小菜一碟了~因为最小公倍数和最大公约数有一个性质：

\[\color{Gray} lcm(A,B)\cdot gcd(A,B) = A \times B \]

即 最小公倍数 × 最大公约数 = 两整数之积。

在已经知道了最大公约数的情况下，利用两整数之积 / 最大公约数即可算出最小公倍数。

PS：关于这个公式的证明就不多说了...

C语言实现

这里的实现很简单，调用一次上面的求最大公约数函数即可。

但是程序中有一点需要注意，最好不要写成两整数之积 / 最大公约数的形式。如果两个整数的数值都很大，在运算过程中很容易发生数据溢出问题。

为了尽可能避免溢出，可以写成 A / 最大公约数 * B 的形式。

long int LCM(long int num1, long int num2) {
    long int divisor = GCD(num1, num2); // GCD 即上面提到的求最大公约数的函数
    num1 = labs(num1); // 一般LCM也被限定为正整数
    num2 = labs(num2);
    return (num1 / divisor) * num2; // A/GCD * B
}

时间复杂度

因为上面的写法实际上是套用了辗转相除算法，所以时间复杂度也是一致的：

\[\color{Gray} O(\log_{}{n}) \]

求多个整数的最小公倍数

和求多个整数的最大公约数一样，可以利用多次二元迭代运算来实现。

C语言实现

long int ArrLCM(long int *arr, int arrLen) {
    long int temp = arr[0];
    int i;
    for (i = 1; i < arrLen; i++) // 从第二个元素开始遍历
        temp = LCM(temp, arr[i]); // LCM是上面提到的求最小公倍数的函数
    return temp;
}

时间复杂度

同上面求多个整数最大公约数的一致：

\[\color{Gray} O(n\log_{}{n}) \]

总结

脑袋一热写了这样一篇笔记。写的过程中咱深刻体会到了咱在证明公式方面能力的缺乏...要继续加油了！

另外可能我对辗转相除法时间复杂度的理解有些许问题，希望大家能予以指正。

相关文章

• 辗转相除法介绍 - 林择枝
• 辗转相除法 - Wikipedia