Vanya decided to walk in the field of size n × n cells. The field contains m apple trees, the i-th apple tree is at the cell with coordinates(xi, yi). Vanya moves towards vector (dx, dy). That means that if Vanya is now at the cell (x, y), then in a second he will be at cell 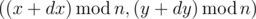 . The following condition is satisfied for the vector:
. The following condition is satisfied for the vector: 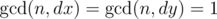 , where
, where 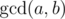 is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.
is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.
Vanya wonders, from what square of the field he should start his path to see as many apple trees as possible.
The first line contains integers n, m, dx, dy(1 ≤ n ≤ 106, 1 ≤ m ≤ 105, 1 ≤ dx, dy ≤ n) — the size of the field, the number of apple trees and the vector of Vanya's movement. Next m lines contain integers xi, yi (0 ≤ xi, yi ≤ n - 1) — the coordinates of apples. One cell may contain multiple apple trees.
Print two space-separated numbers — the coordinates of the cell from which you should start your path. If there are several answers you are allowed to print any of them.
5 5 2 3
0 0
1 2
1 3
2 4
3 1
1 3
2 3 1 1
0 0
0 1
1 1
0 0
In the first sample Vanya's path will look like: (1, 3) - (3, 1) - (0, 4) - (2, 2) - (4, 0) - (1, 3)
In the second sample: (0, 0) - (1, 1) - (0, 0)
好困╯﹏╰,不填坑了,睡觉去。有需要问思路的留言
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int INF = 1e9; const double eps = 1e-6; const int N = 1000010; int cas = 1; struct _node{ int x,y,k; void set(int _k, int _x, int _y) { k = _k; x = _x; y = _y; } }; _node point[N]; int xk[N],cnt[N]; int n,m,dx,dy; void run() { point[0].set(0,0,0); xk[0] = 0; for(int i=1; i<n; i++) { point[i].set(i,(point[i-1].x+dx)%n,(point[i-1].y+dy)%n); xk[point[i].x] = i; } memset(cnt,0,sizeof(cnt)); int x,y,k,y0,yk; while(m--) { scanf("%d%d",&x,&y); k = xk[x]; yk = point[k].y; y0 = (y - yk + n) % n; cnt[y0]++; } int mx=cnt[0], pos=0; for(int i=1;i<n;i++) if(mx < cnt[i]) mx=cnt[i], pos=i; printf("0 %d\n",pos); } int main() { #ifdef LOCAL freopen("case.txt","r",stdin); #endif while(scanf("%d%d%d%d",&n,&m,&dx,&dy)!=EOF) run(); return 0; }
思路:
题目的关键条件是这个 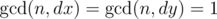
首先想个问题,先是一维的情况下,假设只有一行的格子,长度为x,每次能移动的距离为dx,而且gcd(x,dx)=1,这样手动模拟一下,可以发现规律,从某个点出发直到回到这个点上,步数均为x次,而且每次落下的点都是不重复的,也即这x次的位置覆盖了整条方格上的每一个方格。
那现在二维的情况下,gcd(n,dx) = gcd(n,dy) = 1,也就是从某一行和某一列的交点出发,要重新回到这个交点,就要经过n步而且这n步覆盖了每一行每一列。每个循环必须每个x走一次以及每个y走一次,n个格子属于一组循环里面的,总共有n*n个格子,所以有n组循环。一组循环内的格子是等价的。同一行内的n个格子均来自不同的n组。
现在考虑一组特殊的循环,这组循环从(0,0)开始出发
走了第一步以后就到 (dx%n, dy%n)
第二步到 (2*dx%n, 2*dy%n)
第k步到 (k*dx%n, k*dy%n)
用一个对应关系存储,从(0,0)出发的,经过了k步以后,会到达位置(x[k] , y[k])。
然后考虑普遍的情况了,每组循环都比如经过(0, y0)这个点
从这个点出发的第一步 (dx%n, (y0+dy)%n)
第k步到 (dx%n, (y0+dy)%n), 也即(x[k], (y0+y[k])%n)
那么现在给你某个坐标(x,y),要怎么算出他属于哪一组循环的呢
根据等式x[k]==x,可以求出对应的k的值
那就能求出对应的y[k]了,然后y0+y[k]==y → y0=y-y[k]
这样就知道这个(x,y) 是属于 (0,y0)这一组的了
那么算法大概是这样:
预处理出x[k],y[k],时间复杂度o(n)
遍历每一个apple的坐标(x,y),求出对应的坐标(0,y0),然后cnt[y0]++,复杂度o(m)
找出值最大的cnt[y],答案就是(0,y)了。 总复杂度o(n+m)
代码如上。


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号