Tomash keeps wandering off and getting lost while he is walking along the streets of Berland. It's no surprise! In his home town, for any pair of intersections there is exactly one way to walk from one intersection to the other one. The capital of Berland is very different!
Tomash has noticed that even simple cases of ambiguity confuse him. So, when he sees a group of four distinct intersections a, b, cand d, such that there are two paths from a to c — one through b and the other one through d, he calls the group a "damn rhombus". Note that pairs (a, b), (b, c), (a, d), (d, c) should be directly connected by the roads. Schematically, a damn rhombus is shown on the figure below:
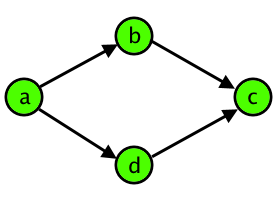
Other roads between any of the intersections don't make the rhombus any more appealing to Tomash, so the four intersections remain a "damn rhombus" for him.
Given that the capital of Berland has n intersections and m roads and all roads are unidirectional and are known in advance, find the number of "damn rhombi" in the city.
When rhombi are compared, the order of intersections b and d doesn't matter.
The first line of the input contains a pair of integers n, m (1 ≤ n ≤ 3000, 0 ≤ m ≤ 30000) — the number of intersections and roads, respectively. Next m lines list the roads, one per line. Each of the roads is given by a pair of integers ai, bi (1 ≤ ai, bi ≤ n;ai ≠ bi) — the number of the intersection it goes out from and the number of the intersection it leads to. Between a pair of intersections there is at most one road in each of the two directions.
It is not guaranteed that you can get from any intersection to any other one.
Print the required number of "damn rhombi".
5 4
1 2
2 3
1 4
4 3
1
4 12
1 2
1 3
1 4
2 1
2 3
2 4
3 1
3 2
3 4
4 1
4 2
4 3
12
题意: 就是找有多少个四点组合符合图中那样的。
思路: 注意到一点,虽然n比较大,有3000个,在满载情况下m的数量可以达到3000*2999=9000000,但是m是比较小的只有30000。
所以完全可以遍历一遍边而花费代价不高。
想着想着就想到一种方法。。不算什么算法。。也不难实现的
用一个结构体edge保存每条边的起点和终点,再用一个邻接矩阵保存某个点到某个点是否有边连通。
再用一个数组 c[x][y] 保存 有多少种方法,是 x 经过一个点再到 y的,这样子以x和y为端点的菱形的数量就是 c[x][y]*(c[x][y]-1)/2 了
遍历一次边集,对于每条边,起点终点分别为x和y,然后遍历一下z,看z是否与x相连,相连的话,则c[z][y]++,这一步需要o(m*n)
统计完以后遍历一次c矩阵,用上面的公式操作矩阵之和就是答案了,这一步需要o(n*n)
总复杂度大概在10^8左右,ok
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int INF = 1e9; const double eps = 1e-6; const int N = 3010; const int M = 30010; int cas = 1; struct _edge{ int u,v; }edge[M]; bool g[N][N]; int c[N][N]; int n,m; void run() { memset(g,0,sizeof(g)); memset(c,0,sizeof(c)); for(int i=0;i<m;i++) { scanf("%d%d",&edge[i].u,&edge[i].v); g[edge[i].u][edge[i].v]=1; } for(int i=0;i<m;i++) { int &x=edge[i].u; int &y=edge[i].v; for(int z=1;z<=n;z++) if(z!=x && z!=y && g[z][x]) c[z][y]++; } int ans = 0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i!=j && c[i][j]) ans+=c[i][j]*(c[i][j]-1); printf("%d\n",ans/2); } int main() { #ifdef LOCAL freopen("case.txt","r",stdin); #endif while(scanf("%d%d",&n,&m)!=EOF) run(); return 0; }


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号