三:变换,量化与熵编码
第6章 变换编码
1. 变换编码
-
变换编码的目的
- 去除空间信号的相关性
- 将空间信号的能力集中到频域的一小部分低频系数上
- 能量小的系数可通过量化去除,而不会严重影响重构图像的质量
-
块变换和全局变换
- 块变换:离散余弦变换(Discrete Cosine Transform,DCT),4x4,8x8,16x16
- 全局变换:小波变换(Wavelet)
-
变换的能量集中特性
- DCT编码
2. 变换类型
- K-L变换
- 傅里叶变换
- 余弦变换
- 小波变换
3. KL变换
- 最优变换
- 基函数根据具体图像而确定
- 没有快速算法
-
实际中很少使用
- 复杂度极高



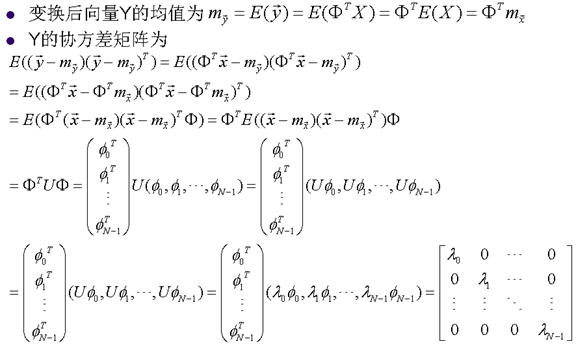

-
K-L变换非常复杂度很高,不实用
- 需要计算协方差矩阵U
- 需要计算特征向量
- 需要发送 到解码器
4. 离散傅立叶变换

5. 离散傅立叶变换性质


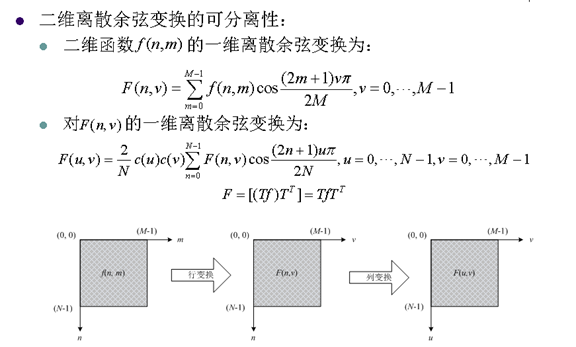
6. 离散余弦变换
- 比K-L变换,傅里叶变换的复杂度更低
- 变换性能仅次于K-L变换
- 有快速算法可以加快变换速度
- 可以用整数变换进一步降低复杂度
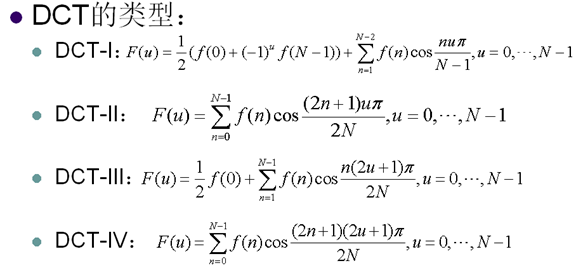



7. DCT与DFT的关系

8. 离散余弦变换的重要性质

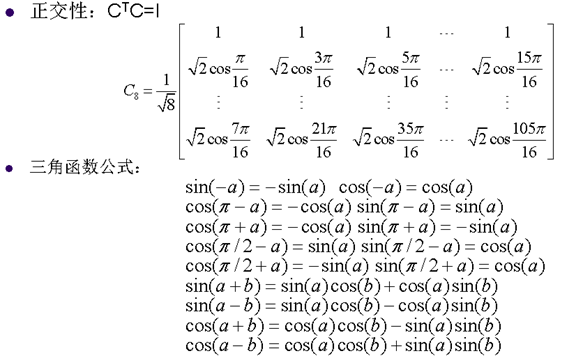
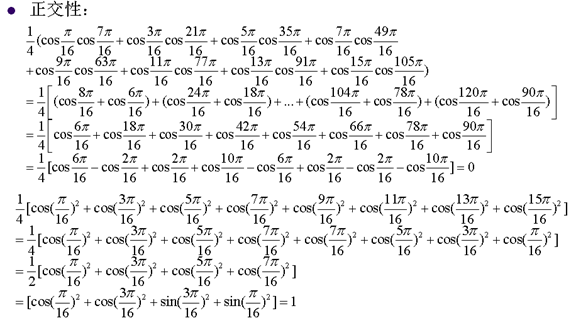
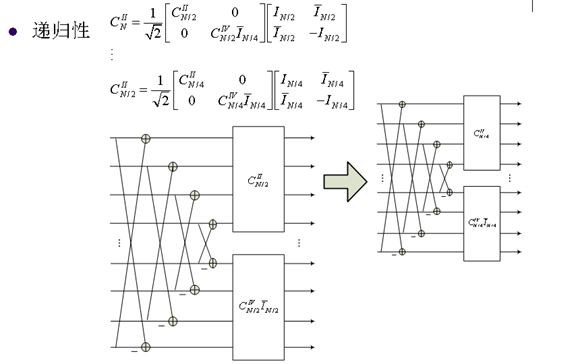
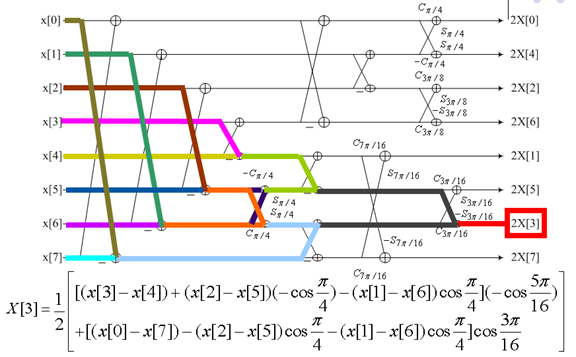
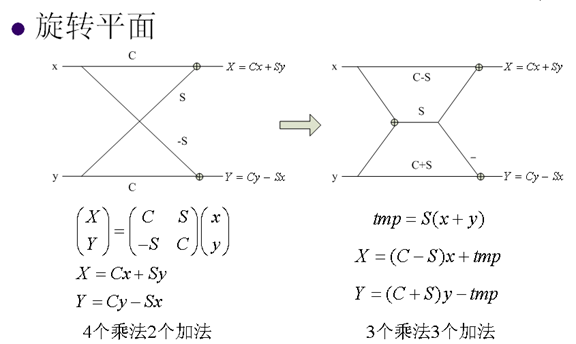
9. 快速DCT变换

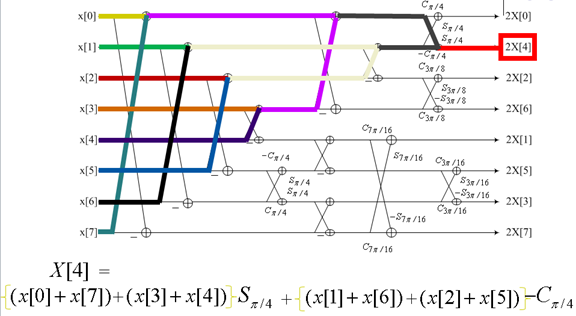
下图是一个动态展示:

10. 整数离散余弦变换
-
离散余弦变换为浮点操作
- 需要64位精度
- 浮点计算复杂度高
- 变换精度高
-
整数变换:离散余弦变换的整数近似
- 需要更少的位宽
- 整数计算复杂度低
- 好的整数变换的变换精度接近浮点变换
- 浮点近似方法

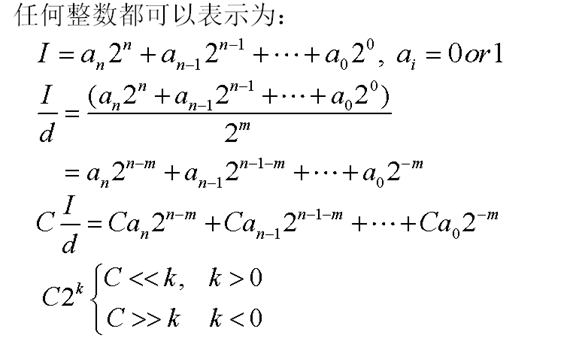

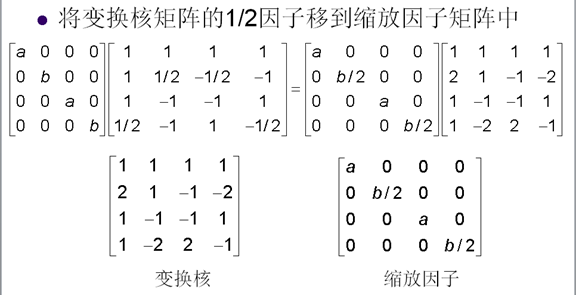
11. H.264的4x4整数变换



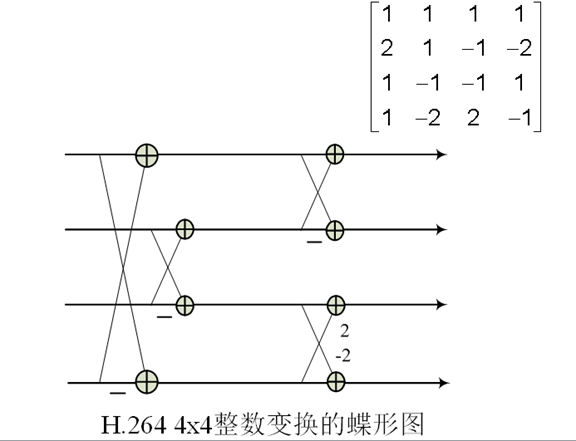



12. 小波变换
- 新的变换方法
- 避免由于块编码带来的块效应
- 更适合视频空间可分级编码
第7章 量化
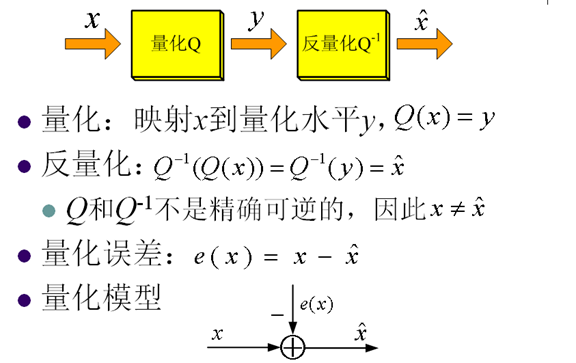
1. 量化Quantization
-
用更小的集合表示更大的集合的过程
- 对信号源的有限近似
- 有损过程
-
应用
- A/D转换
- 压缩
-
量化方法
- 标量(Scalar)量化
- 矢量(Vector)量化
2. 量化的基本思想
- 映射一个输入间隔到一个整数
- 减少信源编码的bit
- 一般情况重构值与输入值不同
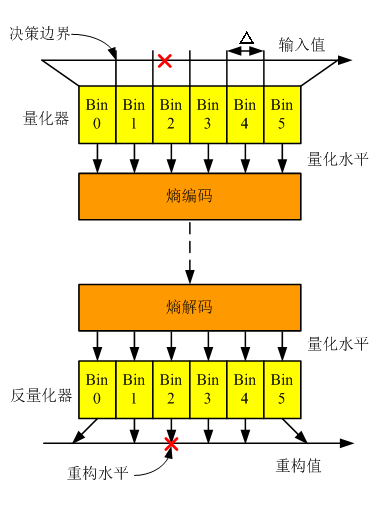
3. 量化模型
4. 量化的率失真优化
-
量化器设计问题
- 量化水平的个数,即Bin的个数
- 决策边界:Bin的边界
- 重构水平
-
量化器设计是对率失真的优化
- 为了减少码率的大小,需要减少Bin的个数
- Bin的个数减少导致重构的误差增大,失真也就随着增大

5. 失真测量

6. 量化器设计
-
量化器设计的两个方面
- 给定量化水平数目M,找到决策边界xi和重构水平 使MSE最小
- 给定失真限制D,找到量化水平数目M,决策边界xi和重构水平yi使MSE<=D

7. 均匀量化(Uniform Quantization)
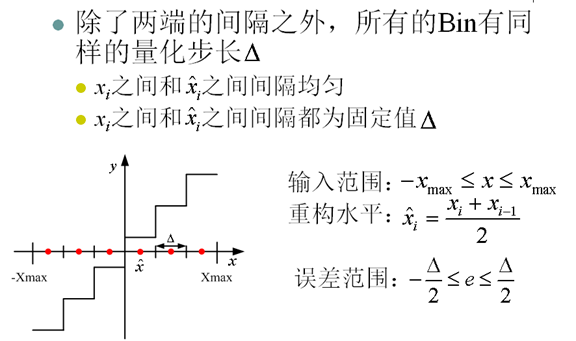
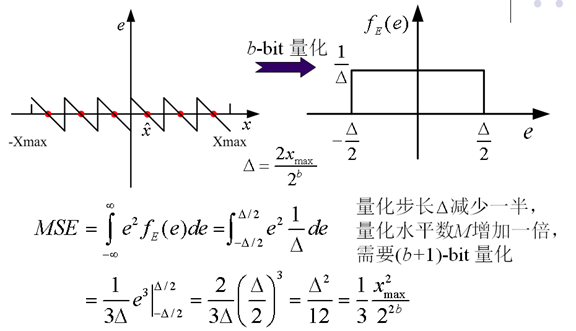
8. 量化与峰值信噪比


9. 中升量化器(Midrise Quantizer)

10. 中平量化器(Midtread Quantizer)
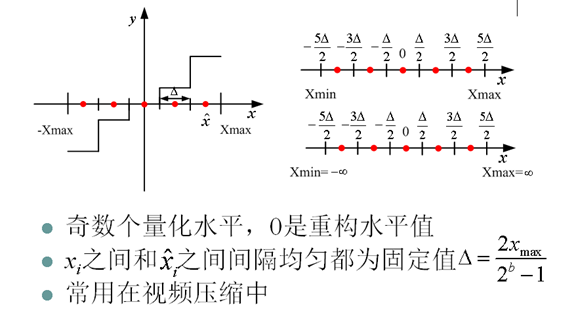
11. 死区量化器(Deadzone Quantizer)
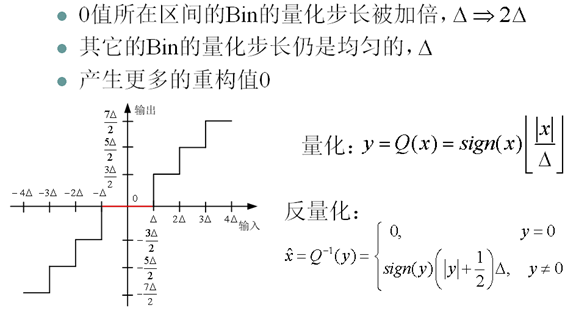
12.非均匀量化(Non-uniform Quantization)
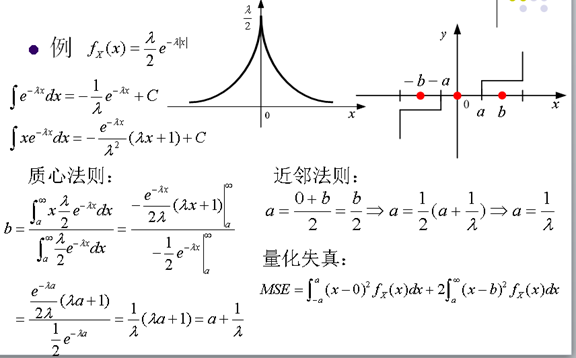
- 如果信源不是均匀分布的,采用均匀量化不是最优的
- 对于非均匀量化,为了减少MSE,当概率密度函数fX(x)高时,使Bin的量化步长减小,当概率密度函数fX(x)低时, 使Bin的量化步长增加。

13. 最优的标量量化
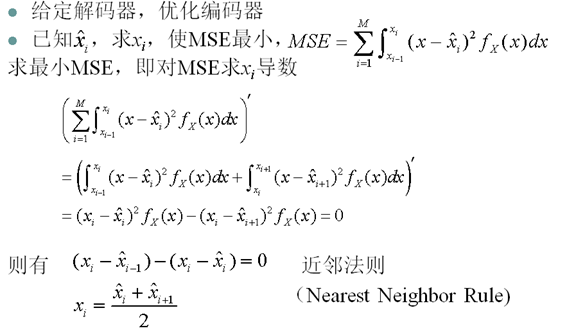

14. 量化编码
-
定长编码量化水平
- 使用等长的码字编码每个量化水平,码字长为:
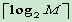
- 使用等长的码字编码每个量化水平,码字长为:
-
熵编码量化水平
- 根据量化水平的概率分布情况,用变长的码字编码每个量化水平
- 平均码字长
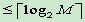
- 比定长编码量化水平效率高
- 广泛应用在图像和视频编码中
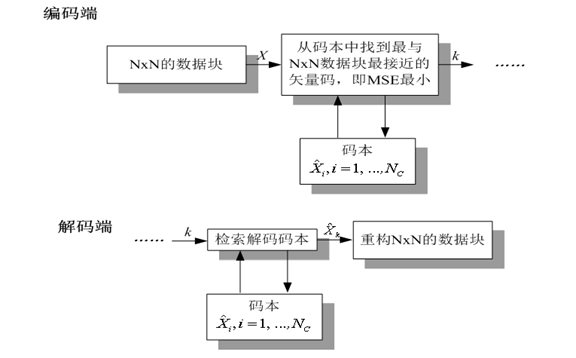
15. 矢量量化
- 标量量化:对数据一个一个的进行量化,称为标量量化。
-
矢量量化:将数据分组,每组K个数据构成K维矢量,再以矢量为处理单元进行量化。
- 矢量量化是标量量化的多维扩展
- 标量量化是矢量量化的特殊情况
- 矢量量化工作过程

- 二维矢量量化
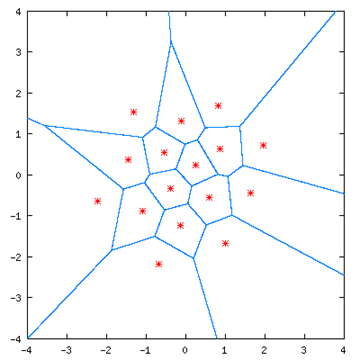
-
矢量量化优点
- 只传码字的下标,编码效率高
- 在相同码率下,比标量量化失真小
- 在相同失真下,比标量量化码率低
- 矢量量化缺点:复杂度随着维数的增加呈指数增加
第8章 熵编码
1. 熵编码
-
熵(Entropy):信源的平均信息量,更精确的描述为表示信源所有符号包含信息的平均比特数
- 信源编码要尽可能的减少信源的冗余,使之接近熵
- 用更少的比特传递更多的信源信息
-
熵编码:数据压缩中根据信源消息的概率模型使消息的熵最小化
- 无损压缩
- 变长编码
2. 熵
- 信息量:
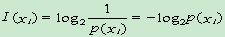
单位:比特
- 熵:
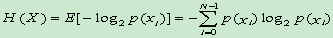
单位:比特/符号


3. 定长编码

4. 变长编码
-
变长编码:用不同的比特数表示每一个符号
- 为频繁发生的符号分配短码字
- 为很少发生的符号分配长码字
- 比定长编码有更高的效率
-
常用的变长编码
- Huffman编码
- 算术编码
5. Huffman编码
-
前缀码:任何码字不是其它码字的前缀
- 如果011为一个有效码字,则0,1,01,11必不是有效码字
- 不会引起解码歧义
-
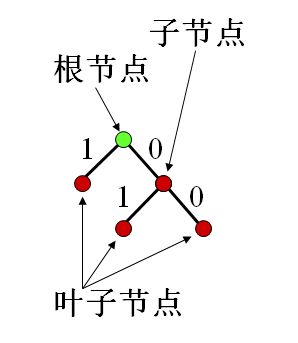
Huffman:
- 二叉树
- 树节点:表示符号或符号组合
- 分支:两个分支一个表示"0",另一个表示"1"
-
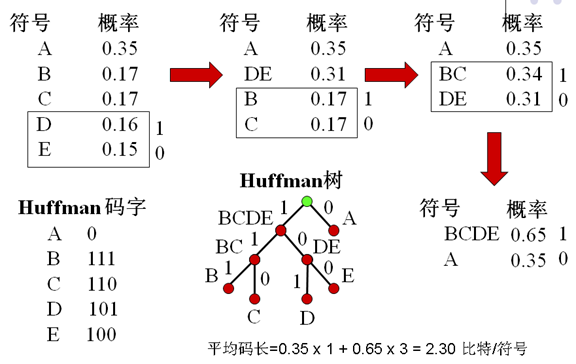
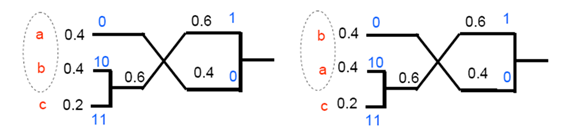
Huffman的不唯一性
-
每次分支有两种选择:0,1

-
相同的概率产生不同的组合
-
-
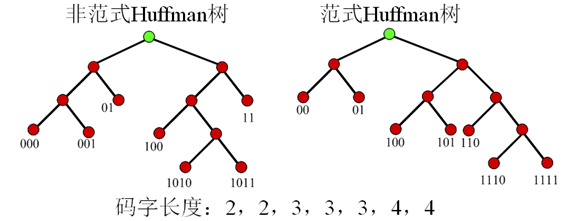
缺点:
- 数据的概率变化难于实时统计
- Huffman树需要编码传输给解码器
- 只有在p(xi)=1/2ki 时是最优编码
- 最小码字长度为1比特/符号
-
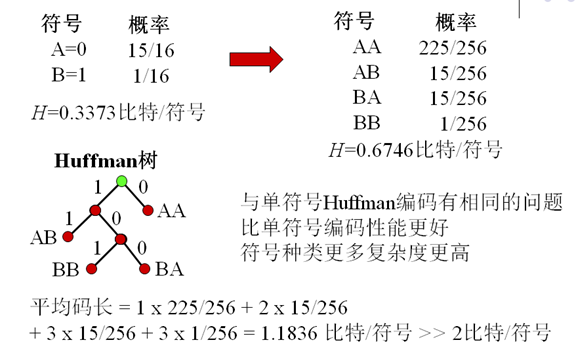
如果有二值信源,其两个符号的概率相差很大
- 例如:p(1)=0.0625,p(0)=0.9375则H=0.3373比特/符号,Huffman编码平均码长=1比特/符号
- 两个符号联合编码有更高效率
6. 扩展Huffman编码
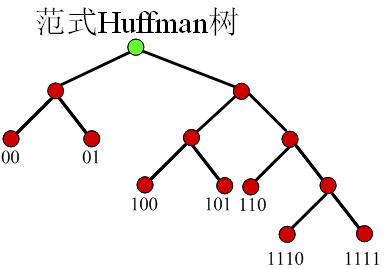
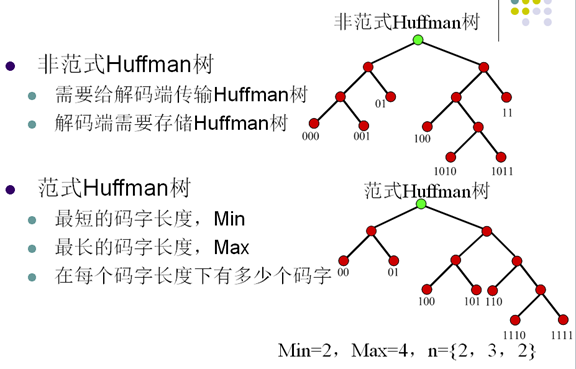
7. 范式Huffman编码
-
范式Huffman树的建立规则
- 节点左支设为0,右支设为1
- 树的深度从左至右增加
- 每个符号被放在最先满足的叶子节点
-
特性
- 第一个码字是一串0
- 相同长度的码字的值是连续的
- 如果所有的码字通过在低位补0的方式,使所有码字的长度相同则有 0000<0100<1000<1010<1100<1110<1111
-
从码字长度n到n+1有如下关系
- C(n+1,1)=(C(n,last)+1)<<1
-
从码字长度n到n+2有如下关系
- C(n+2,1)=(C(n,last)+1)<<2
8. 一元码
- 编码一个非负整数n为n个1和一个0
- 不需要存储码表
-
可以用Huffman树表示
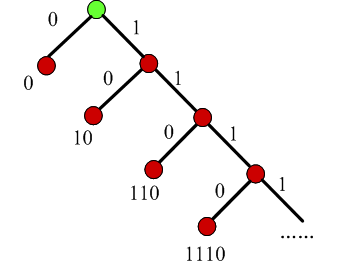
- 码长增长太快:n=100,码长101

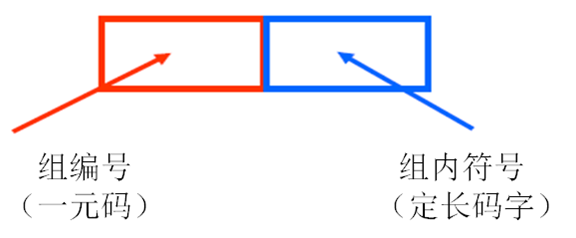
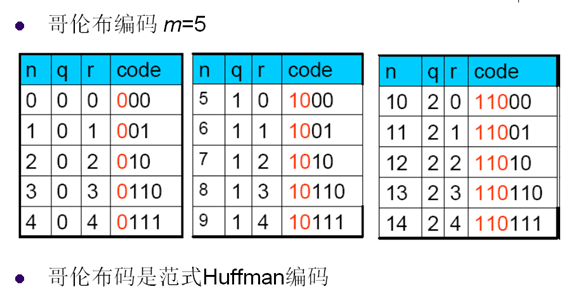
9. 哥伦布编码
- 将信源符号等分成几组,每组有相应的编号
- 编号小的分配码字短,编号大分配码字长
-
同组的符号有等长的码字,比一元码的码字长度增长慢

- 码字分配

10. 指数哥伦布编码
- 哥伦布码对信源符号的分组大小相同
- 指数哥伦布码对信源符号的分组大小按照指数增长
- 指数哥伦布码依然是一元码加定长码的形式
- 指数哥伦布码的指数k=0,1,2,…



11. CAVLC( Context-Based Adaptive Variable Length Code)
-
当前块的系数分布和其邻块的系数分布情况相关
-
NX为块X的非零系数个数,当前块C的第一个系数的编码码表由NC决定, NC=( NA+ NB )/2
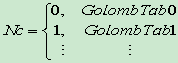
-
-
当前待编码系数和前面编码系数有相关性
- 当前块C的其它系数的编码码表由前一个系数的幅值决定cofN-1=>GolombTab_x,用GolombTab_x编码cofN

12. 算术编码
- 信息量=>符号编码比特数
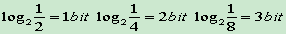
- Huffman编码为每个符号分配一个码字,这说明Huffman编码的压缩上限是1比特/符号
- 算术编码若干个符号可编码成1bit
-
算术编码是把信源表示为实数轴上[0,1]区间,信源中每个符号都用来缩短这个区间
- 输出[0,1]区间的一个实数表示一串编码符号
- 比Huffman编码更有效
-
编码思想
- 编码器用熵编码算法编码一串符号产生一个[0,1]区间的实数,将实数的一个二进制表示传给解码器
- 解码器用熵解码算法解码得到一串符号
-
小数的二进制表示
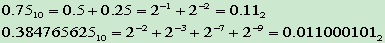
-
信源符号概率分布
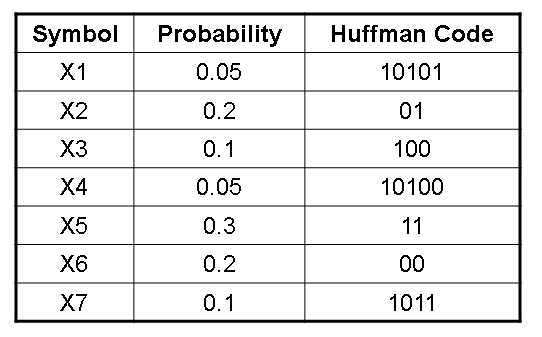
- 字符串:X2 X2 X3 X3 X6 X5 X7
- Huffman编码,01 01 100 100 00 11 1011,18bit
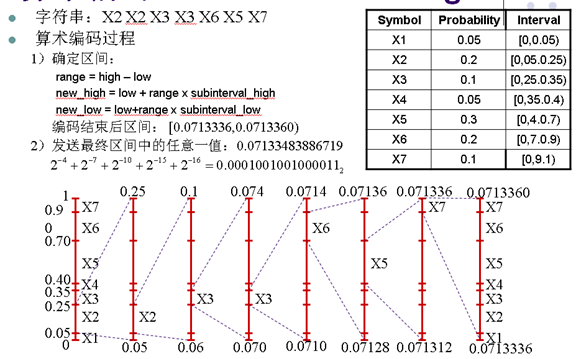
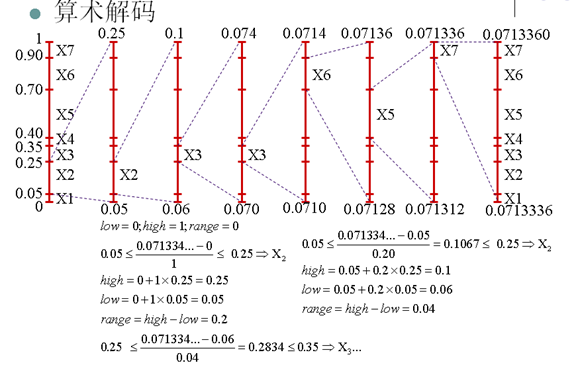
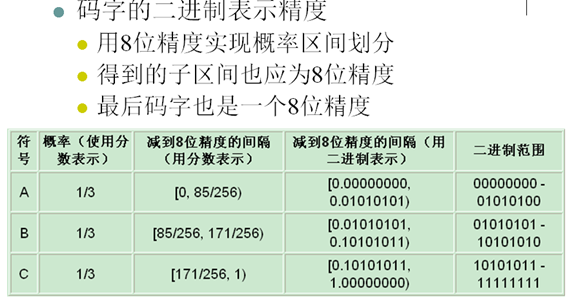
- 算术编码更接近熵
- 有限精度算术编码是次优(Near-optimal)编码,发送整数比特给解码端
- 算术编码到最后一个字符编码结束才输出码字
- 编码复杂度也比较高
13. 二值算术编码

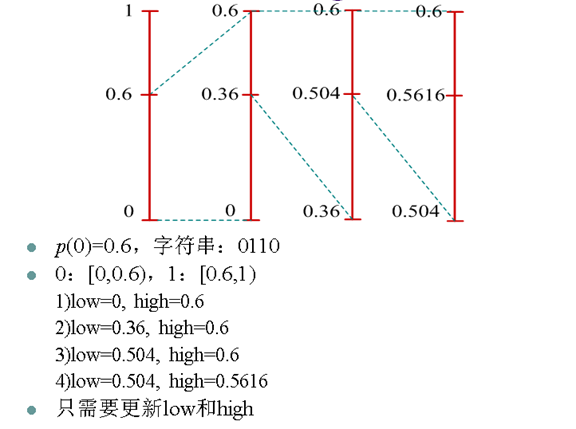

13. 自适应二值算术编码
- 由于信源0和1出现的概率是在不断变化的,因此0和1的概率区间也应该不断改变
- 自适应二值算术编码每编码一个0或1都重新统计0和1的概率并重新划分[0,1)区间
- 编解码端的概率统计模型一致,能够得到同样的[0,1)区间划分


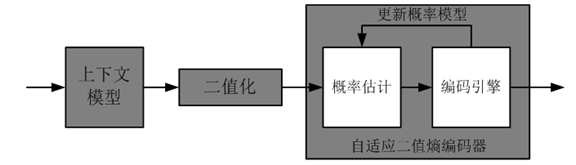
14. CABAC(Context-Based Adaptive Binary Arithmetic Coding)
-
当前块的语法元素概率分布和其邻块的语法元素概率分布情况相关
- 当前块C的邻块A和B的语法元素SA与SB可以为编码C块的语法元素SC选择概率模型
-
二值化
- 将语法元素值转换成二进制值串
-
概率模型更新
- 根据已经编码的比特,重新估计二进制值串的概率并更新概率模型,用新的概率模型编码下一个比特
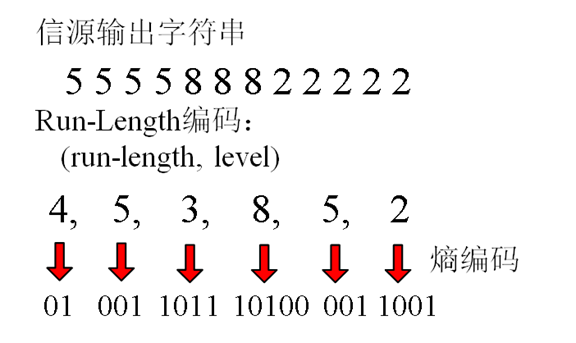
15. Run Length 编码
- 利用信源字符的重复性来编码的技术
- 对有很长,很多重复字符的信源编码非常有效
- 重复字符称为run,重复的字符个数称为run length
- Run-length编码能够和其它熵编码一起来压缩数据

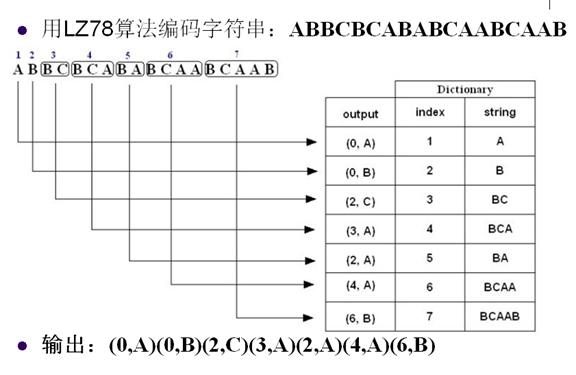
16. 字典编码
-
字典编码:根据信源符号(消息)的组合特点,建立包含各种符号组合的字典,编码这些符号组合的索引
- LZ78=>Winzip
- LZW=> GIF
- 适合一般意义上的数据压缩,去除数据的统计冗余
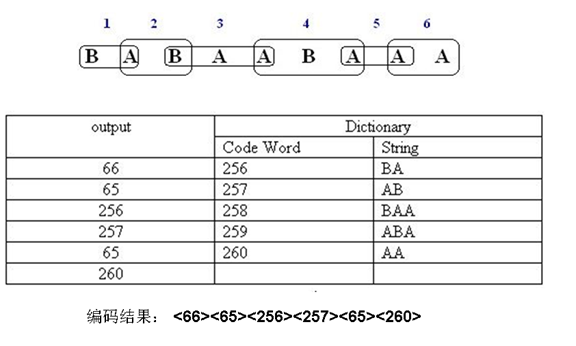
17. LZW
- 将信源输出的字符串中,每个第一次出现的字符或者字符串用索引来表示,并将字符或字符串对应的索引编码到码流中
- 解码端根据从码流中解码的字符,在线的建立和编码器完全一样的字典,并恢复出信源输出的字符串
- 适用于字符串中有大量的子字符串多次重复出现,重复次数越多,压缩效果越好
- 单个符号被分配为0-255之间的值
- 初始码表,使其包含值为0-255的256个符号,值大于255的符号为空
- 编码器将根据编码的符号情况确定字符组合为从 256 到 4095 之间的值
- 编码时,编码器识别新的字符组合,并将他们增加到码表中
- 编码器用码表中的符号组合所对应的值编码
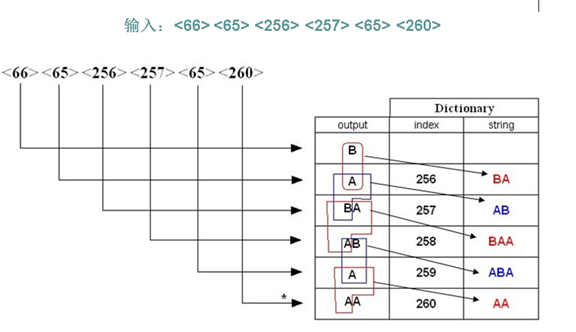
- 解压时LZW解码器能够产生和编码器完全一样的码表
- 和编码器一样先初始化所有的单字符,将0-255之间的值分配给它们
- 除了解码第一个字符外,解码其它字符时都要更新码表
- 通过读码字并根据码表中的值将它们解码为对应的字符或字符组合
18. LZ78