二维逆运动学 – 代码

介绍

在本系列的前一部分中，我们讨论了具有两个自由度的机械臂的反向运动学问题；如下图所示。

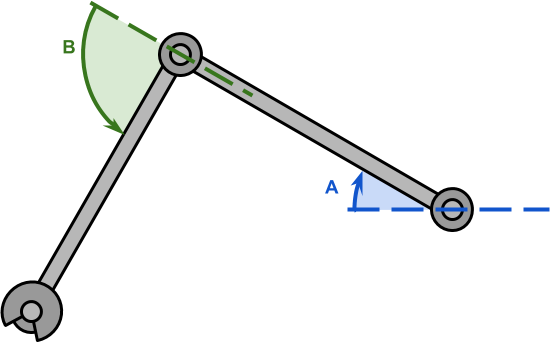
在这种情况下，机械臂的长度c和 一个通常是已知的。如果我们必须到达的点是 C，那么配置就变成了一个三角形，其中所有边都是已知的。

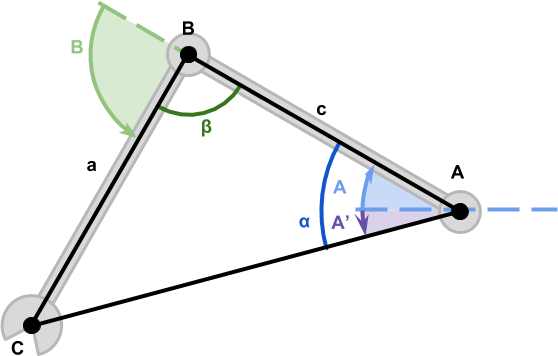
然后，我们推导出了角度和一个B的方程，它控制着机械臂关节的旋转：

 

 \begin{equation*} A = \underset{\alpha}{\underbrace{\cos^{-1}{\left(\frac{b^2+c^2-a^2}{2bc}\right)}}} + \underset{A'}{\underbrace{\tan^{-1}{\left(\frac{C_Y-A_Y}{C_X-A_X}\right)}}} \end{equation*}　　　　（1）

 \begin{equation*} B = \pi - \underset{\beta}{\underbrace{\cos^{-1}{\left(\frac{a^2 + c^2 -b^2}{2ac}\right)}}} \end{equation*}　　　　　　　　　　　　　　（2）

 

 

乍一看，它们可能看起来相当吓人;另一方面，从上图来看，它们的几何解释应该非常直观。

创建机械臂

实施此解决方案的第一步是创建机械臂。“关节”的概念不是Unity附带的。但是，可以利用引擎提供的父类系统来创建与机械臂完全相同的组件层次结构。

我们的想法是为每个关节使用一个GameObject，这样旋转它的变换就会导致附着在它上面的手臂也随之旋转。将第二个关节连接到第一个关节将导致它们旋转，如第一张图所示。 

生成的层次结构将变为：

  • Root
    • Joint A
      • Bone A
      • Joint B
        • Bone B
        • Hand

然后，我们可以向根对象添加一个名为SimpleIK的脚本，它将负责旋转关节以达到所需的目标。

 1 using System.Collections;
 2 using UnityEngine;
 3 
 4 namespace AlanZucconi.IK
 5 {
 6     public class SimpleIK : MonoBehaviour
 7     {
 8         [Header("Joints")]
 9         public Transform Joint0;
10         public Transform Joint1;
11         public Transform Hand;
12 
13         [Header("Target")]
14         public Transform Target;
15 
16         ...
17     }
18 }

 

在本教程的前一部分推导的方程需要知道前两个骨骼的长度(分别称为 c 和 一个)。因为骨骼的长度不应该改变，所以它可以在Start函数中计算。然而，这要求手臂在游戏开始时处于良好的配置状态。

1 private length0;
2 private length1;
3 
4 void Start ()
5 {
6     length0 = Vector2.Distance(Joint0.position, Joint1.position);
7     length1 = Vector2.Distance(Joint1.position, Hand.position  );
8 }

 

旋转关节

在显示代码的最终版本之前，让我们从一个简化的版本开始。如果我们将等式 （1） 和 （2） 直接转换为代码，我们最终会得到这样的结果：

 1 void Update ()
 2 {
 3     // Distance from Joint0 to Target
 4     float length2 = Vector2.Distance(Joint0.position, Target.position);
 5 
 6     // Inner angle alpha
 7     float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
 8     float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;
 9 
10     // Inner angle beta
11     float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
12     float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;
13 
14     // Angle from Joint0 and Target
15     Vector2 diff = Target.position - Joint0.position;
16     float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;
17 
18     // So they work in Unity reference frame
19     float jointAngle0 = atan - angle0;    // Angle A
20     float jointAngle1 = 180f - angle1;    // Angle B
21 
22     ...
23 }

数学函数 cos^{-1} 和 tan^{-1} 在 Unity 中称为 Mathf.Acos和Mathf.Atan2，此外，最终角度也转换为度数Mathf.Rad2Deg，由于Transform组件接受度数，而不是弧度。

瞄准无法实现的目标

虽然上面的代码似乎有效，但存在失败的情况。如果无法访问目标，会发生什么情况？目前的实施没有考虑到这一点，导致了不良行为。

一种常见的解决方案是将手臂完全伸展到目标方向。这种行为与我们试图模拟的伸展运动是一致的。

下面的代码通过检查与根部的距离是否大于手臂的总长度来检测目标是否遥不可及。

 1 void Update ()
 2 {
 3     float jointAngle0;
 4     float jointAngle1;
 5 
 6     float length2 = Vector2.Distance(Joint0.position, Target.position);
 7 
 8     // Angle from Joint0 and Target
 9     Vector2 diff = Target.position - Joint0.position;
10     float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;
11 
12     // Is the target reachable?
13     // If not, we stretch as far as possible
14     if (length0 + length1 < length2)
15     {
16         jointAngle0 = atan;
17         jointAngle1 = 0f;
18     }
19     else
20     {
21         float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
22         float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;
23 
24         float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
25         float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;
26 
27         // So they work in Unity reference frame
28         jointAngle0 = atan - angle0;
29         jointAngle1 = 180f - angle1;
30     }
31 
32     ...
33 }

 

旋转关节

现在剩下的就是旋转关节。这可以通过访问关节的Transform组件的localEulerAngles属性，不过很遗憾，无法直接更改角度，因此需要复制、编辑和替换矢量。

1 Vector3 Euler0 = Joint0.transform.localEulerAngles;
2 Euler0.z = jointAngle0;
3 Joint0.transform.localEulerAngles = Euler0;
4 
5 Vector3 Euler1 = Joint1.transform.localEulerAngles;
6 Euler1.z = jointAngle1;
7 Joint1.transform.localEulerAngles = Euler1;

 

结论

这篇文章结束了 2D 机械臂的逆运动学课程。

您可以在此处阅读此在线课程的其余部分：

此外，还提供以 3D 为重点的后续产品：

本教程中介绍的线条艺术动物的灵感来自WithOneLine的作品。

下载

您可以下载本教程中使用的所有资源，以便为 Unity 提供功能齐全的机械臂。

posted @ 2024-03-15 10:45  soliang  阅读(81)  评论(0)  编辑  收藏  举报