二维逆运动学 – 数学
介绍
我们习惯于与周围的世界互动,因此很容易低估移动我们的手和手臂到底有多复杂。在学术文献中,控制机械臂的任务被称为逆运动学。运动学代表运动,而反向是指我们通常不控制手臂本身的事实。我们控制的是旋转每个关节的电机。反向运动学是决定如何驱动这些电机将手臂移动到某个位置的任务。就其一般形式而言,这是一项极具挑战性的任务。为了感受它的挑战性,您可以考虑 QWOP、GIRP 甚至 Lunar Lander 等游戏,在这些游戏中,您不决定去哪里,而是决定激活哪些肌肉(或推进器)。
控制移动执行器的任务甚至早于机器人领域。几个世纪以来,数学家和工程师一直在开发无数的解决方案,这并不奇怪。大多数 3D 建模软件和游戏引擎(包括 Unity)都带有一组工具,可以绑定类人和类狗的生物。对于所有不同的设置(如机械臂、尾巴、触手、翅膀等),通常不提供内置解决方案。
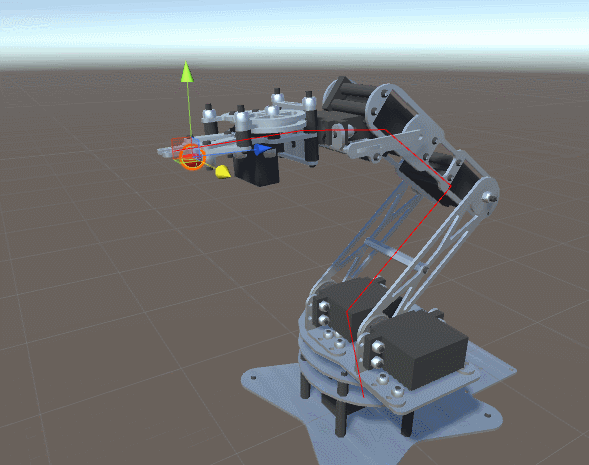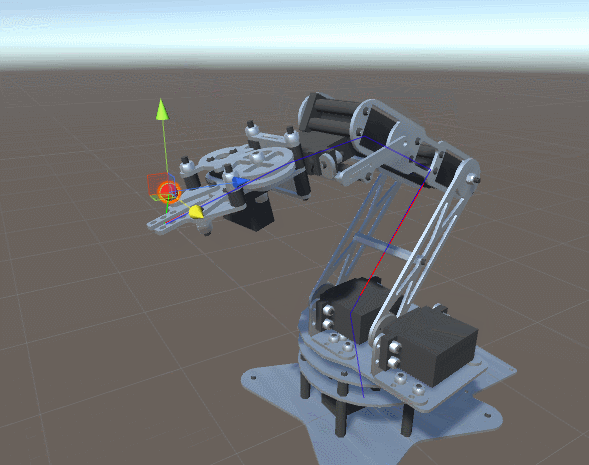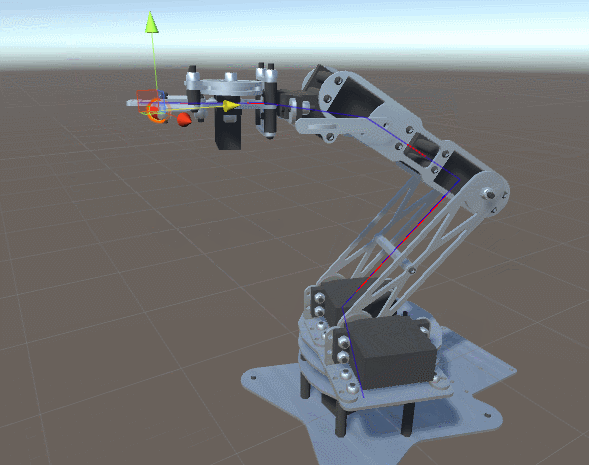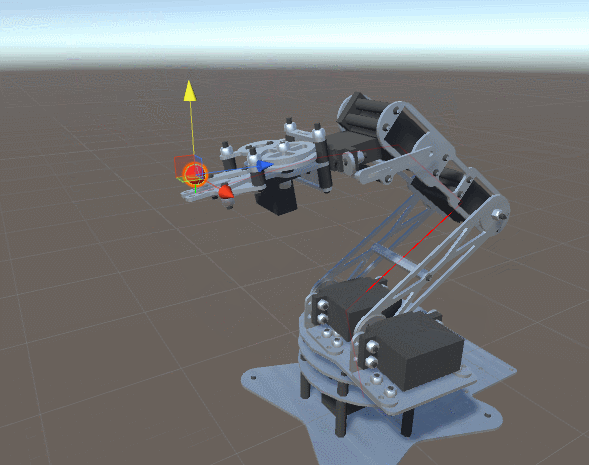
这就是为什么在之前关于程序动画和逆向运动学的系列中,我介绍了一个非常通用且有效的解决方案,它可能适用于任何设置。但这种力量是有代价的:效率。该系列受到的主要批评之一是,它太耗时且昂贵,无法同时用于数百个角色。这就是为什么我决定开始一个新系列,专门研究具有两个自由度的手臂的反向运动学。您将在本教程中发现的技术非常高效,并且可以同时在数十个(如果不是数百个)字符上运行。
逆向运动学
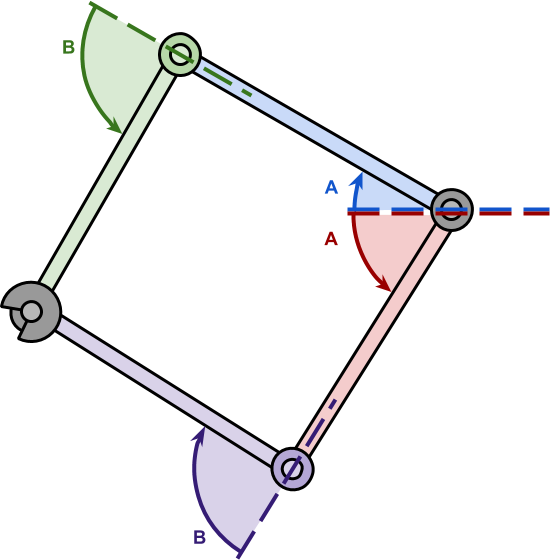
让我们想象一个有两个节段和两个关节的机械臂,如下图所示。在手臂的末端,有我们想要控制的末端执行器。我们无法直接控制末端执行器的位置;我们只能旋转关节。逆运动学的问题是找到旋转关节以将末端执行器移动到所需位置的最佳方法。
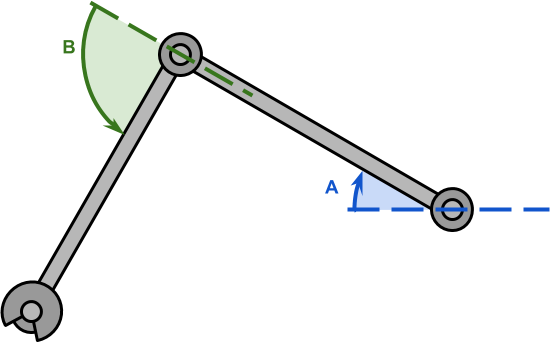
这个新系列中提出的解决方案仅适用于具有两个关节的机械臂。在学术文献中经常说,这些机械臂有两个自由度。通过查看下图,其原因将非常清楚。具有两个自由度的机械臂可以建模为三角形,这是几何学中研究最多的几何图形之一。
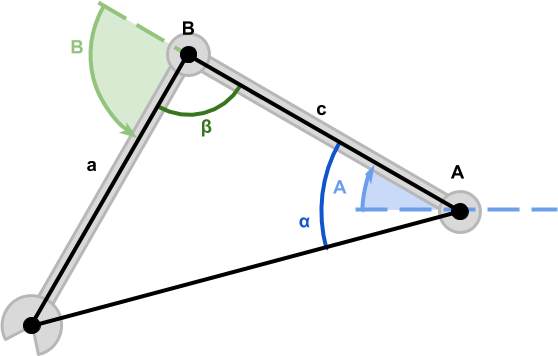
让我们先把问题形式化一点。两个关节
和(均为黑色)可以分别旋转
(蓝色)和
(绿色)度。这会导致末端执行器移动到一个位置
。
内角
我们可以使用这三个点,
并
构造一个具有内角的三角形
,
和
,如下图所示。

虽然这三个角度是未知的,但我们知道所有边的长度。
- 该段
表示手臂并具有长度
;
- 该段
代表前臂,长度
;
- 该段
表示肩关节和手之间的距离,并具有长度
。
知道三角形的三个边就足以找到它的所有角度。这要归功于余弦定律,这是毕达哥拉定理对不一定成直角的三角形的推广。
控制机械臂所需的两个角度是 和
。让我们从
开始,它可以使用余弦定律计算:
(1)
我们可以参考(1)来提取:
现在需要的是使用反余弦函数(也称为弧线)来找到
:
(2)
用同样的程序,我们可以再次应用余弦定律来发现:
(3)
给我看看余弦定律的推导!
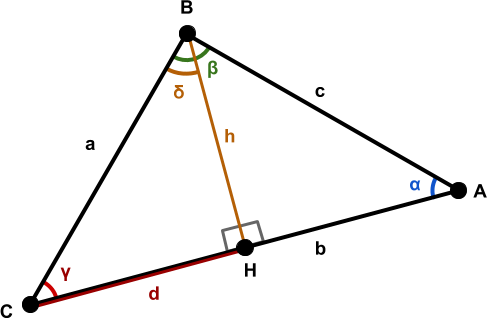
该段将三角形
分为两个直角三角形:
和
。这个证明是将毕达哥拉定理应用于两个三角形的自然结果:
(4)
(5)
(4) 和 (5) 现在都用 表示。我们可以将它们等同于获得:
可以重新命名为:
(6)
等式(6)是余弦定律在欧几里得的命题12中从《元素》第2卷中转录的方式。
为了得到方程的现代形式,我们需要应用一些三角学。由于(5)是直角三角形,我们可以将线段表示为:
(7)
通过记住三角形的角总和为(或等效的
弧度)可以找到:
(8)
代入(7),我们得到:
(9)
最后一步是众所周知的协同功能恒等式的结果,该恒等式指出:
我们现在可以使用(9)来代替(6),这给了我们余弦定律的现代形式:
(10)
关节角度
使用余弦定律,我们计算了 和
的值,它们是机械臂创建的三角形的内角。但是,我们真正需要的角度是
(蓝色)和
(绿色)。
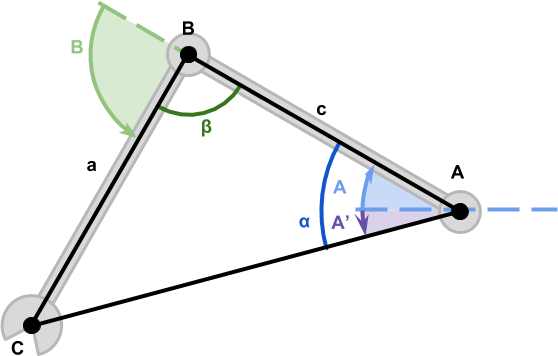
让我们从计算开始,这更容易。从上图可以明显看出,
总
和为
(等于
弧度)。这意味着:
(11)
计算没有太大区别。这里唯一的区别是我们需要考虑
(紫色),这是段
的角度。这可以使用 arcotangent 函数
计算:
(12)
这导致:
(13)
角度的符号,
并且大多
是任意的,取决于每个关节的运动方式。
多种解决方案?
下一步...
这篇文章结束了对具有两个自由度的机械臂的逆运动学数学的介绍。
下一篇文章将探讨如何使用推导的方程在Unity中有效地移动机械臂。
您可以在此处阅读此在线课程的其余部分:
此外,还提供以 3D 为重点的后续产品:
- 第 3 部分:三维逆运动学
本教程中介绍的线条艺术动物的灵感来自WithOneLine的作品。
下载
您可以下载本教程中使用的所有资源,以便为 Unity 提供功能齐全的机械臂。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!