一、前言
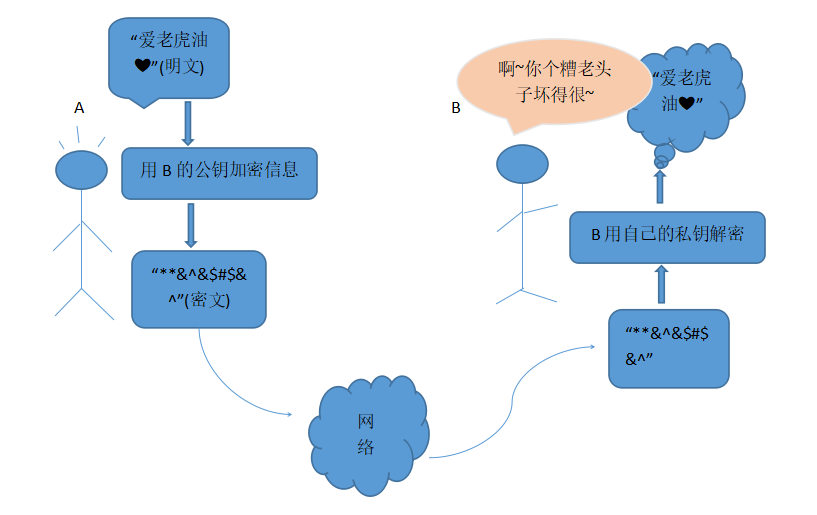
RSA算法是一种非对称的加密算法,它通常是先生成一对RSA密钥,其中之一是保密密钥(私钥),由用户保存;另一个为公开密钥(公钥),
可对外公开;要加密传输内容时,比如A要给B传输信息,此时A先用B的公钥将内容加密后传输,B收到A传输过来的信息后用自己的私钥解密.
![]()
该过程中,只要B不泄露自己的私钥,那么就算第三方截取到了该信息,没有B的私钥也无法解密获得内容信息.
RSA算法的安全性依赖于大数分解,计算两个大素数的乘积很容易,但是反过来由该乘积分解成两个素数相乘,如果该乘积够大的话,分解的难
度是极其大的.正式进入RSA算法的讨论之前,先来了解一下欧拉函数、欧拉定理、模反元素.
二、欧拉函数
2.1 什么是欧拉函数
欧拉函数是小于x的整数中与x互素的数的个数,一般用φ(x)表示。特殊的,φ(1)=1.
2.2 如何计算欧拉函数
通式:φ(n)=n*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)*…*(1-1/pn),其中p1, p2……pn为n的所有素因数,n是不为0的整数.
2.3 欧拉函数的一些性质
1. 对于素数p,φ(p)=p−1
2. 若p为素数,n=p^k,则φ(n)=p^k-p^(k-1)
3. 欧拉函数是积性函数,但不是完全积性函数;若m,n互素,则φ(m∗n)=φ(m)∗φ(n),特殊的,当m=2,n为奇数时,φ(2*n)=φ(n)
4. 当n>2时,φ(n)是偶数
5. 小于n的数中,与n互素的数的总和为:φ(n) * n / 2 (n>1)
6. n=∑d∣nφ(d),即n的因数(包括1和它自己)的欧拉函数之和等于n
三、欧拉定理
欧拉定理是指:如果两个正整数a和n互素,则n的欧拉函数φ(n)可以让下面的式子成立:
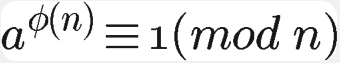
即a的φ(n)次方减去1,可以被n整除. 比如,3和4互质,φ(4)=2,(3^2-1)/4=2. 当a为正整数,n为素数且a不能被n整除时,则有
a^(n-1) ≡ 1 (mod n)
这就是费马小定理.
四、模反元素
如果两个正整数a和n互素,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1. 这时,b就叫做a对模数n的模反元素.
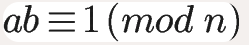
欧拉定理可以用来证明模反元素必然存在,如下图,可以看到:a的 φ(n)-1 次方,就是a对模数n的模反元素.
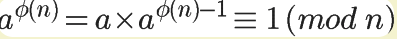
五、RSA算法
5.1 密钥的生成过程
- 1. 随意选择两个大的素数p和q,p不等于q,计算n = pq.
- 2. 根据欧拉函数的性质3,求得r=φ(n)=φ(p)φ(q)=(p-1)(q-1).
- 3. 选择一个小于r的整数e,且e与r互素;并求得e关于r的模反元素,命名为d.(模反元素存在,当且仅当e与r互质; 求d令ed≡1(mod r))
- 4. 将p和q的记录销毁
其中(n,e)是公钥,(n,d)是私钥. 例如:
- 1. A随机选两个不相等的质数61和53,并计算两数的积n=61*53=3233,n的长度就是密钥长度。3233的二进制是110010100001,一共12位,
- 所以这个密钥就是12位. 实际应用中,RSA密钥一般是1024位,重要的场合是2048位.
- 2. 计算n的欧拉函数; φ(n)=(p-1)(q-1)=60*52=3120.
- 3. A在1到3120上随机选择了一个随机数e=17,与3120互素.
- 4. 计算e对φ(n)的模反元素d,即时,ed-1=kφ(n)。
- 即使求解:17x+3120y=1.用扩展欧几里得算法求解。可以算出一组解(x,y)=(2753,-15),即d=2753. 公钥(3233, 17),私钥(3233,2753)
至此完成计算.
5.2 RSA的可靠性
在RSA私钥和公钥生成的过程中,共出现过p,q,n,φ(N),e,d,其中n,e组成公钥,其他的都不是公开的,一旦d泄露,就等于私钥泄露;
那么能不能根据n,e推导出d呢?
1. ed ≡ 1(mod φ(n)) 只有知道e和φ(n),才能算出d
2. φ(n)=(p-1)(q-1) 只有知道p和q,才能算出φ(n)
3. n=pq,只有将n分解才能算出p和q
所以,只有将n素因数分解,才能算出d; 也就意味着私钥破译. 但是,大整数的质因数分解是非常困难的. 所以理论上来说,如果我们找到
了快速对大整数进行质因数分解的方法,那么RSA加密也就没什么安全性可言了;遗憾的是,目前数学上并没有找到这样快速的质因数分解方法.
5.3 RSA的加密过程
假设A要向B发送加密信息m,他就要用B的公钥(n,e)对m进行加密,但m必须是整数(字符串可以取ascii值或unicode值),且m必须小
于n. 所谓加密就是计算下式的c:
m^e ≡ c (mod n)假设m=65,B的公钥(3233,17),所以等式如下:
65^17≡2790(mod 3233)所以c等于2790,A就把2790发给B.
5.4 RSA的解密过程
B收到A发来的2790后,就用自己的私钥(3233,2755)进行解密
c^d ≡ m (mod n)也就是c的d次方除以n的余数就是m
2790^2753 ≡ 65 (mod 3233)因此得到原文65.
六、解密可靠性的证明
即证明由 c^d ≡ m (mod n) (1)解密出的m一定是正确的消息.
证明: 加密公式为 m^e ≡ c (mod n),由该公式可以得到
c = m^e - nk (2)
将(2)代入(1)中,可以得到
(m^e - nk)^d ≡ m (mod n)
简化之,得到:
m^(ed) ≡ m (mod n)(3)
已知:ed ≡ 1(mod φ(n)),由该式子可以得到
ed = hφ(n)+1 (4)
将(4)代入(3)中,可以得到
m^(hφ(n)+1) ≡ m (mod n) (5)
只要证明(3)(或(5))成立即可. 接下来分为 m、n 互素和 m、n 不互素两种情况讨论
I. m、n互素
由欧拉定理可以知道 m^φ(n) ≡ 1 (mod n)
证明:m^(hφ(n)) ≡ 1 (mod n)
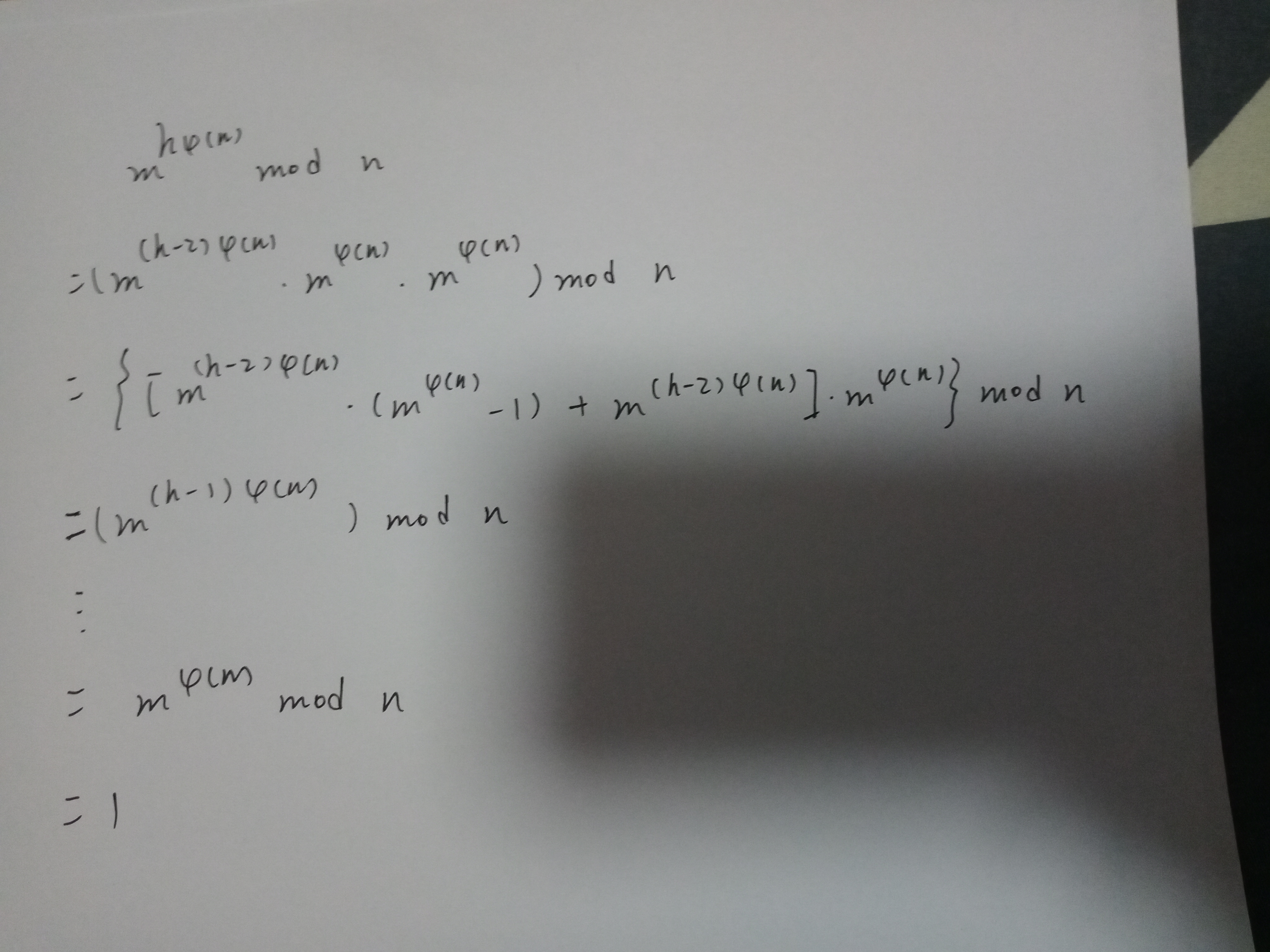
即
m^(hφ(n)) ≡ 1 (mod n)
即
(m^(hφ(n)))*m ≡ m (mod n)
即
m^(hφ(n)+1) ≡ m (mod n)
所以当m、n互素时(5)成立.
II. m、n不互素
由于n=pq,且p、q均为素数,由欧拉定理,有:
(p)^(q-1) ≡ 1 (mod q)
又m、n不互素,则必有m=kp或m=kq;以 m = kp为例,此时k、p必然互素,又由欧拉定理,有:
(k)^(q-1) ≡ 1 (mod q)
证明:(kp)^(q-1) ≡ 1 (mod q)
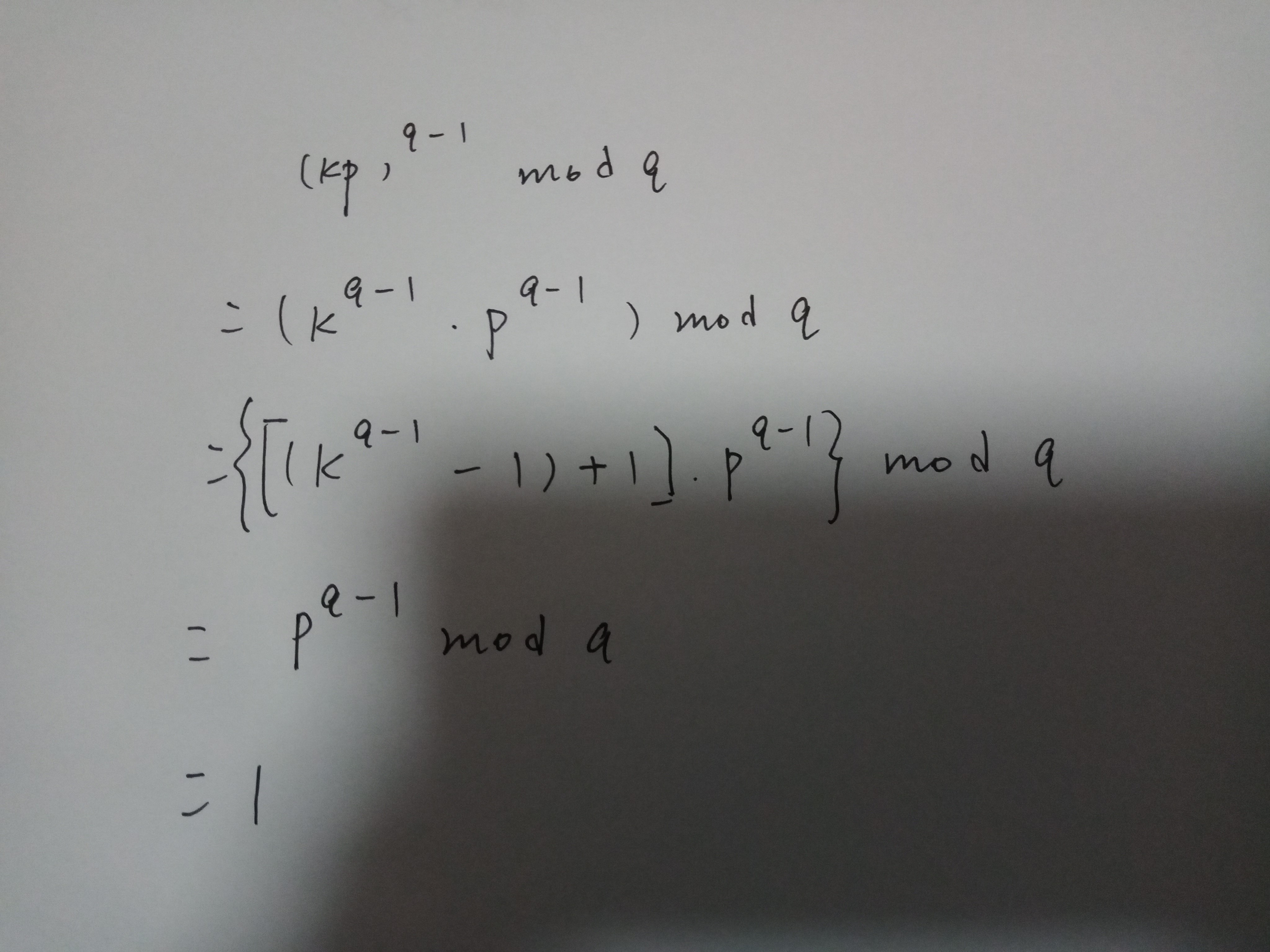
即 (kp)^(q-1) ≡ 1 (mod q),进一步得到
[(kp)^(q-1)]^[h(p-1)] × kp ≡ kp (mod q)
即
(kp)^(ed) ≡ kp (mod q)
即
(kp)^(ed) = kp + tq
两边同时除以p,得到
[(k)^(ed)]*[(p)^(ed-1)] = k + (tq)/p
这时t必然能被p整除,即 t=t'p
(kp)^(ed) = t'pq + kp
因为 m=kp,n=pq,所以
m^(ed) ≡ m (mod n)
于是(3)得到证明. 证毕!
七、参考资料
https://blog.csdn.net/liuzibujian/article/details/81086324 https://blog.csdn.net/qq_36056315/article/details/7990229 https://baike.baidu.com/item/模反元素/20417595?fr=aladdin https://blog.csdn.net/gao131360144/article/details/79966094 http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号