Step 4: Rebalance

Step 4: Rebalance

Now we have to write code to rebalance when it becomes necessary. We'll use rotations to do this, as before. Again, we'll distinguish the cases on the basis of x's balance factor, where x is y's right child:

173. <Step 4: Rebalance after AVL deletion 173> =
struct avl_node *x = y->avl_link[1];
if (x->avl_balance == -1)
  { 
    <Left-side rebalancing case 1 in AVL deletion 174> 
  }
else 
  { 
    <Left-side rebalancing case 2 in AVL deletion 175> 
  }

This code is included in 172.

Case 1: x has - balance factor

If x has a - balance factor, we handle rebalancing in a manner analogous to case 2 for insertion. In fact, we reuse the code. We rotate right at x, then left at y. w is the left child of x. The two rotations look like this:

174. <Left-side rebalancing case 1 in AVL deletion 174> =
struct avl_node *w;
<Rotate right at x then left at y in AVL tree 159>
pa[k - 1]->avl_link[da[k - 1]] = w;

This code is included in 173.

Case 2: x has + or 0 balance factor

When x's balance factor is +, the needed treatment is analogous to Case 1 for insertion. We simply rotate left at y and update the pointer to the subtree, then update balance factors. The deletion and rebalancing then look like this:

When x's balance factor is 0, we perform the same rotation, but the height of the overall subtree does not change, so we're done and can exit the loop with break. Here's what the deletion and rebalancing look like for this subcase:

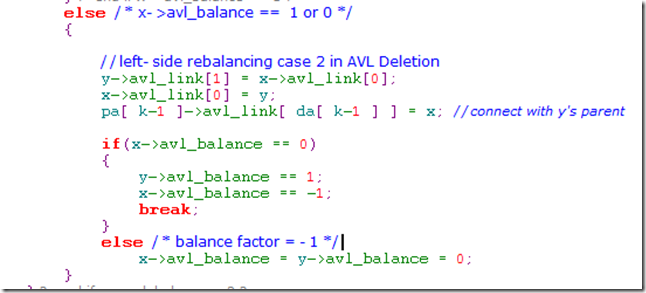
175. <Left-side rebalancing case 2 in AVL deletion 175> =
y->avl_link[1] = x->avl_link[0];
x->avl_link[0] = y;
pa[k - 1]->avl_link[da[k - 1]] = x;
if (x->avl_balance == 0) 
  {
    x->avl_balance = -1;
    y->avl_balance = +1;
    break;
  }
else 
  x->avl_balance = y->avl_balance = 0;

This code is included in 173.

Exercises:

1. In <Step 4: Rebalance after AVL deletion 173>, we refer to fields in x, the right child of y, without checking that y has a non-null right child. Why can we assume that node x is non-null? [answer]

A: Tree y started out with a + balance factor, meaning that its right subtree is taller than its left. So, even if y's left subtree had height 0, its right subtree has at least height 1, meaning that y must have at least one right child.

2. Describe the shape of a tree that might require rebalancing at every level above a particular node. Give an example. [answer]
A:

Rebalancing is required at each level if, at every level of the tree, the deletion causes a +2 or -2 balance factor at a node p while there is a +1 or -1 balance factor at p's child opposite the deletion.

For example, consider the AVL tree below:

Deletion of node 32 in this tree leads to a -2 balance factor on the left side of node 31, causing a right rotation at node 31. This shortens the right subtree of node 28, causing it to have a -2 balance factor, leading to a right rotation there. This shortens the right subtree of node 20, causing it to have a -2 balance factor, forcing a right rotation there, too. Here is the final tree:

Incidentally, our original tree was an example of a “Fibonacci tree”, a kind of binary tree whose form is defined recursively, as follows. A Fibonacci tree of order 0 is an empty tree and a Fibonacci tree of order 1 is a single node. A Fibonacci tree of order n >= 2 is a node whose left subtree is a Fibonacci tree of order n - 1 and whose right subtree is a Fibonacci tree of order n - 2. Our example is a Fibonacci tree of order 7. Any big-enough Fibonacci tree will exhibit this pathological behavior upon AVL deletion of its maximum node.