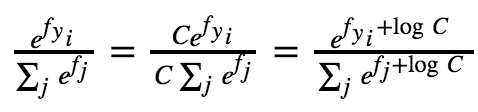深度学习中得数学,高效计算基础与线性分类器
深度学习说到底就是要调节网络中得权重,使网络的分类结果更接近于训练值。这个重复迭代的过程又是一个线性回归的问题。在这种可能会用到高数,线性代数,概率论中的知识。
一、数学基础提一提。
1.高数中得知识。
高数中最重要的就是微积分了,那在深度学习中出现最多的一个概念就是梯度。什么是梯度呢?要说导数,学过高数的肯定都知道。其实梯度就是当把标量x变成向量X时,对X求导就是梯度。那为什么要用梯度呢?因为梯度等于0在凸函数中往往代表着一个极小值点。我们要求得就是损失函数的极小值,这正是我们需要的。梯度是指向函数最大增加的方向,下面来解释为什么。

往往我们直接去求梯度等于0并不容易,所以我们要一步一步迭代,当f(x)无限接近于0.当X(k)=梯度,此时等式右边就变成一个二范式,这就代表了函数的最大增加方向。当我们对梯度取负时,就变成了函数减小最快的方向。也就是我们常说的梯度下降方法。工程中会在梯度前乘一个常数用来控制变化的程度,通常被称为步长。
2.概率论
(1)其中用的较多的知识是:独立变量概率的表示形式有分布函数,概率密度估计函数,累积分布函数
(2)中心极限定理
(3)贝叶斯公式
3.PCA:一种算法,用来对矩阵降维使用。
二、神经网络简介与应用
1.图像上的应用
(1)场景识别
(2)图片内容识别
(3)自动图片归类
(4)拍立淘
2.自然语言上的应用
把一些文本输入到RNN会自动学习。例如把小四的文章输入网络中,可以自动学习其文笔输出文字。
3.综合应用
把在图像和文本上的应用结合起来。例如输入一张图片,输出对这张图片的描述。
三、高效计算基础
1.Python的数据类型,可参考另一篇博文http://www.cnblogs.com/softzrp/p/6523336.html
2.Python中的库:numpy和scipy
四、图像识别 其实就是输入一个多维数组,每一个位置的数都是0-255的范围,都代表一个颜色
1.困难之处:
(1)视角不同:一张图片经过旋转或者侧视后构图是完全不同的,计算机很难识别。(这也是一个好处,当样本量不够时可以通过旋转等方式增加样本量)
(2)尺寸大小不统一
(3)变形
(4)光影等干扰
(5)背景干扰
(6)同类内的差异
2.数据驱动学习,不是先去定义一个规则
3.K最近邻法
(1)需要衡量样本间的距离(曼哈顿距离,欧式距离,余弦距离)
(2)k最近邻法:找到训练集中最近的N个,以他们中出现的最多的结果作为结果
(3)N折交叉验证:把训练集分成N分,用其中N-1份做训练,第i份做测试得到一个准确率,最后把这n个准确率求平均。当N取不同的值会得到多个不同的平均准确率,取最大的那个平均准确率对应的n值
4.KNN做识别的优缺点
(1)准确度不高
(2)要记录全部训练数据
(3)慢
5.线性分类器
(1)得分函数:f(x,W)=Wx+b 其中x为输入的一个列向量,W为权重矩阵。举个例子:一张图片是32*32*3(长宽为32个像素,3位通道)的,那就可以构建一个32*32*3=3072维的一个列向量,把他作为x输入。假如要分为10类,那么W就是一个10*3072的一个矩阵。W*x后得出一个10*1的一个列向量f,把它作为得分函数。
理解:1)看做一条直线对空间划分 2)模板匹配:w的每一行可以看做是其中一个类别的模板;每类得分,实际上是像素点和模板匹配度;模板匹配的方式是内积运算
(2)损失函数(代价函数/cost function)(客观度/object)
给定W,可以由像素映射到类目得分,可以调整参数/权重W,使得映射的结果和实际类别吻合,损失函数是用来衡量吻合度的
损失函数 1:hinge loss/支持向量机损失
对于训练集中的第i张图片数据x i,在W下会有一个得分结果向量f(x i ,W), 第j类的得分为我们记作f(x i ,W) j, 则在该样本上的损失我们由下列公式计算得到
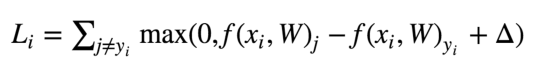

因为是线性模型,因此可以简化成
![]()

加正则化项:
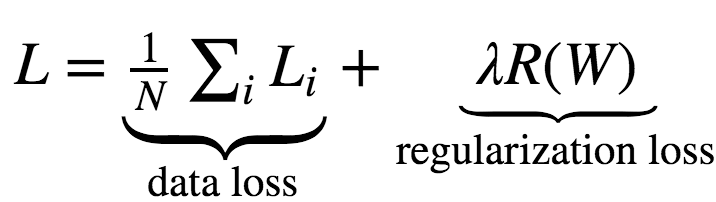
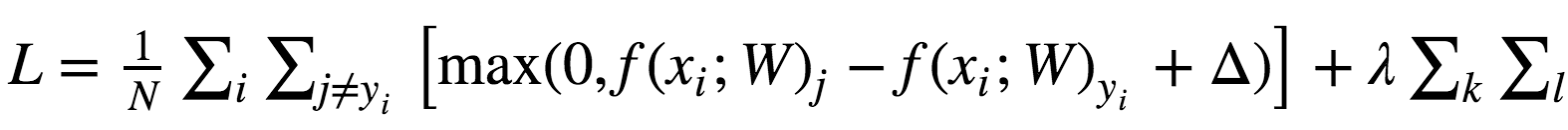
损失函数2: : 互熵损失(softmax)
对于训练集中的第i张图片数据x i,在W下会有一个得分结果向量f yi,则损失函数记作

或者
![]()
其中一般: