小学四则运算结对项目报告【GUI】
结对项目报告【GUI】
博客一览
一、仓库地址
二、预计PSP
三、结对编程对接口的设计
四、计算模块接口的设计与实现过程
五、计算模块接口部分的性能改进
六、计算模块部分单元测试展示
七、计算模块部分异常处理说明
八、界面模块的详细设计过程
九、界面模块与计算模块的对接
十、结对过程的描述
十一、结对编程的优缺点
十二、完成后实际的PSP
十三、项目总结与改进
一、仓库地址
代码仓库地址:https://git.coding.net/Siamese_miao/team.git
二、预计PSP
|
PSP |
任务内容 |
计划共完成需要的时间(h) |
|
Planning |
计划 |
0.5 |
|
Estimate |
估计这个任务需要多少时间,并规划大致工作步骤 |
0.5 |
|
Development |
开发 |
39.25 |
|
Analysis |
需求分析 (包括学习新技术) |
0.5 |
|
Design Spec |
生成设计文档 |
0.25 |
|
Design Review |
设计复审 (和同事审核设计文档) |
0.25 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
0.25 |
|
Design |
具体设计 |
2 |
|
Coding |
具体编码 |
30 |
|
Code Review |
代码复审 |
1 |
|
Test |
测试(自我测试,修改代码,提交修改) |
5 |
|
Reporting |
报告 |
4 |
|
Test Report |
测试报告(包括博客) |
3 |
|
Size Measurement |
计算工作量 |
0.5 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
0.5 |
三、结对编程对接口的设计
1、在信息隐藏方面
Information hiding is part of the foundation of both structured design and object-oriented design. In structured design, the notion of “black boxes” comes from information hiding. In object-oriented design, it gives rise to the concepts of encapsulation and modularity, and it is associated with the concept of abstraction.
----From Code Complete Section 5.3
在《代码大全》中列出了两类需要隐藏的内容:
第一类信息是复杂化的信息,对于我们的项目而言,对于出题的用户来讲,他不需要知道程序在收到需求后是如何运行的,而对于做题的用户来讲,他不需要知道程序是如何来判题的,信息隐藏将内部的算法实现封装起来,对外部只提供调用的接口,使得程序之间各个模块各司其职,互不影响。
对于第二类,是指变动的信息,比如在用户的输入需求中出现了错误并被抛出,这个错误在类中进行了适当的处理,错误没有扩散,这样可以提高程序的容错性
2、在接口设计方面
在接口的设计过程中,我们尽量贴合实际需求并要求接口避免冗余,接口与接口之间互相独立,使用方便。
3、在松耦合方面
所谓耦合性指的是两个子程序之间联系的紧密程度,子程序之间具有良好耦合的特点是它们之间的耦合是非常松散的,任一个子程序都能很容易地被其它子程序调用,在我们的程序中,每一项功能有独自的存在类,多个类之间可以轻易调用,使用之间互不干扰。整个项目中不存在不合理耦合,使用简单数据耦合与控制耦合。
四、计算模块接口的设计与实现过程
1、 类的设计
(1)Command类:对命令行参数进行分析调用
(2)createFile类:生成对应的文本文件
(3)formula类:根据需求生成对应的算式
(4)calculate类:对算式进行相应的计算
(5)stack类:用于算式计算
2、类中的方法设计
(1) Command类:
a:isInteger(String s)
判断字符串是否为数字
(2) createFile类
a: fileCreate(int n,int lower,int upper,int o,int c,int b)
根据参数生成符合要求的文件
(3) formula类:
a: Bracket_AS(int lower,int upper,int o)
产生有括号的加减算式,调用decide1(),decide(),work();
b: Bracket(int lower,int upper,int o)
产生有括号的四则运算式,调用numberB(),work(),operator();
c: AddSubtract(int lower,int upper,int o)
产生简单加减算式,调用decide1(),decide();
d: Arithmetic(int lower,int upper,int o)
产生四则运算式,调用numberA(),operator(),work();
(4) calculate类
a: numberA(int key,int num,int result,int lower,int upper)
产生无括号情况下的数
b: numberB(int key,int num,int result,int lower,int upper)
产生有括号情况下的数
c: decide0(int x,int min,int max)
产生加数
d: decide1(int x,int min,int max)
产生减数
e: decide2(int x,int min,int max)
产生除数
f: decide3(int x,int min,int max)
产生乘数
g: operator(int num,int middle2,int middle3)
限制乘除法出现条件
(5) stack类
a: work(String s,int lower,int upper,int op)
由中缀表达式转为后缀表达式
b: doCal(int a,int b,String stmp)
判断弹出的符号并计算
3、流程图


五、计算模块接口部分的性能改进
基于原来的个人项目代码,由于出现了运算过程以及运算结果数值范围的限制,原本的result(String temp)不再使用,改用了栈运算。
// 计算结果 public static Object result(String temp) { ScriptEngineManager sem = new ScriptEngineManager(); ScriptEngine se = sem.getEngineByName("js"); Object last = 0; try { last = se.eval(temp); } catch (ScriptException e) { e.printStackTrace(); } return last; }
在栈的运算中加入判断
if (Math.abs(sresulat) > upper || Math.abs(sresulat) < lower) { return 0; }
另外,原本的操作符是一开始随机生成好的再判断选择后一个数,然后再判断符号是否合法,再修改符号,如果还是有小数或负数,则重新运行生成算式的函数,这样使得代码运行有些慢且多次运行。再加上数值范围的限定以及可以存在负数,我改变了想法。
因为负数的存在,使得加减号并没有数字的限制,而乘法有上限限制,除法有下限限制。所以在只有加减的运算中,符号随机生成,后一个数根据运算符以及数值范围生成合法的数。
// 相加不超过范围 public static int decide0(int x, int min, int max) { int y; int temp = 0; if (x > 0) { temp = max - min - x + 1;// 加一个正整数范围 } else { temp = max - (min - x) + 1;// 加至正整数的范围 } if (temp < 0) {// 范围小于0 if (x > 0) { temp = Math.abs(x) - min * 2 + 1;// 正整数过大,需加负数 y = 0 - (int) (Math.random() * temp) - min; } else { temp = Math.abs(x) - 2 * min + 1;// 负数过小,越值,加小整数至负数范围 y = (int) (Math.random() * temp) + min; } } else { y = (int) (Math.random() * temp + min); } return y; } // 相减不小于最小 public static int decide1(int x, int min, int max) { int temp = 0; int y = 0; if (x > 0) { temp = x - 2 * (min - 1) - 1; // 减一个正数范围 } else { temp = max + x - min + 1;// 减一个正数范围 } if (temp > 0) { if (x < 0 && temp < min) { temp = Math.abs(x) - 2 * min + 1;// 负数过小,需减负数 y = 0 - (int) (Math.random() * temp) - min; } else { y = (int) (Math.random() * temp + min); } } else { temp = max - x - min + 1;// 只有x>0的情况会出现,正数过小,需减负数 y = 0 - (int) (Math.random() * temp) - min; } return y; }
当有乘除时,则根据上一个数生成操作符,再根据操作符生成合法的后一位数。
// 操作符的选定 public static int operator(int num, int middle2, int middle3) { if (Math.abs(num) <= middle2) {// 除法下界 if (Math.abs(num) < middle3) { return 3; } else { return 0; } } else if (Math.abs(num) >= middle3) {// 乘法上界 return 2; } else { return (int) (Math.random() * 4); } } // 下一位数字的选定 public static int[] numberB(int key, int num, int lower, int upper) { int[] find = new int[] { 0, lower }; if (key == 0) { find[1] = decide0(num, lower, upper); return find; } else if (key == 2) { int[] judge = new int[2]; judge = decide2(num, lower);// 确保能够整除,并不低于下限 if (judge[0] == 0) { find[1] = judge[1]; return find; } else { find[0] = 1; } } else if (key == 3) { find[1] = decide3(num, lower, upper); if (find[0] == 0) { return find; // 乘法不超过上限 } } find[1] = decide1(num, lower, upper); return find; }
这样大大减少了重新调用函数的问题,并且实现了运算过程与数值皆在范围内的功能。
其中,生成有括号与乘除的式子生成的函数判断耗时最多,因为它的判断较多,限制较多,优先级易改变,容易生成最终不合法的式子而重新运行。
// 带括号的四则运算 public static String Bracket(int lower, int upper, int o) { int middle2 = lower * lower;// 除法下界 int middle3 = upper / lower;// 乘法上界 int brack_left = 0; // 记录未匹配的左括号个数 int brack = 0; // 括号个数 int j = 0; char[] p = new char[] { '+', '-', '÷', '*' }; String temp1 = ""; int[] num = new int[o + 1]; // 数字 int[] key = new int[o]; // 符号所在的下标 num[0] = (int) (Math.random() * (upper - lower + 1) + lower); int result; int[] find = new int[2]; for (j = 0; j < (o - 1); j++) { if (num[j] < 0) { temp1 += "(" + String.valueOf(num[j]) + ")"; } else { temp1 += String.valueOf(num[j]); } int tmpcnt = brack_left; for (int i = 0; i < tmpcnt; i++) { // 若当前有未匹配的左括号,则对每一个未匹配的左括号,都有一定概率生成相应右括号。 if ((int) (Math.random() * 5) > 1) { // 生成右括号概率为0.6 brack_left--; temp1 += ")"; } } key[j] = calculate.operator(num[j], middle2, middle3); find = calculate.numberB(key[j], num[j], lower, upper); if (find[0] == 1) { key[j] = 1; } num[j + 1] = find[1]; temp1 += String.valueOf(p[key[j]]); if (((brack * 2) <= o) && (((int) (Math.random() * 2)) == 0)) { // 以一定概率生成左括号,概率为1/2 temp1 += "("; brack++; brack_left++; j++; if (num[j] < 0) { temp1 += "(" + String.valueOf(num[j]) + ")"; } else { temp1 += String.valueOf(num[j]); } // 生成左括号后必须生成一个数字和运算符,不然可能出现(15)这样的错误 key[j] = calculate.operator(num[j], middle2, middle3); find = calculate.numberB(key[j], num[j], lower, upper); if (find[0] == 1) { key[j] = 1; } num[j + 1] = find[1]; temp1 += p[key[j]]; } } while (j != o) { // 判断是否为最后一个数 if (num[j] < 0) { temp1 += "(" + String.valueOf(num[j]) + ")"; } else { temp1 += String.valueOf(num[j]); } key[j] = calculate.operator(num[j], middle2, middle3); temp1 += p[key[j]]; find = calculate.numberB(key[j], num[j], lower, upper); if (find[0] == 1) { key[j] = 1; } j++; num[j] = find[1]; } if (num[o] < 0) { temp1 += "(" + String.valueOf(num[o]) + ")"; } else { temp1 += String.valueOf(num[o]); } while ((brack_left) != 0) { // 补全右括号 temp1 += ")"; brack_left--; } result = stack.work(temp1, lower, upper, 1); if (result == 0) { temp1 = Bracket(lower, upper, o); } return temp1; } }
在附加题记录用户模块,一开始使用contains(name)函数判断用户,后来发现这样会出现abc与abcabc被认为同一个人而的情况,经过思考,我们使用字符串的断开。
String[] arrays = txt.split(" ");
在使用equals(String)函数判断用户,解决了这个问题。
2、性能分析展示
项目总体分析图,从内存,多线程,CPU等方面分析了计算模块的性能,截图如下

性能分析过程截图:
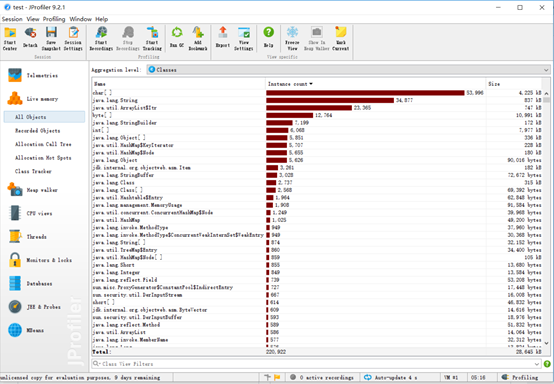



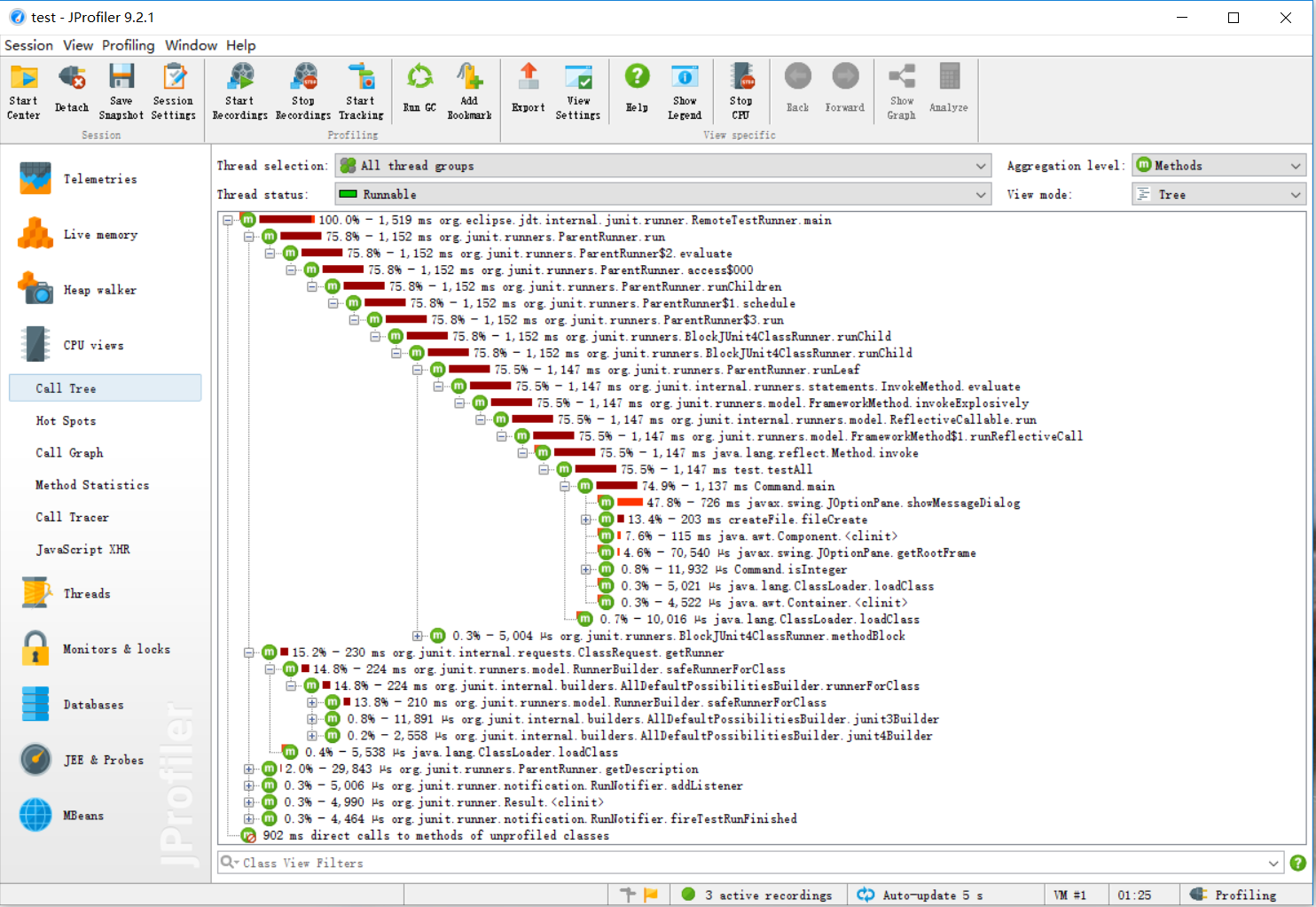
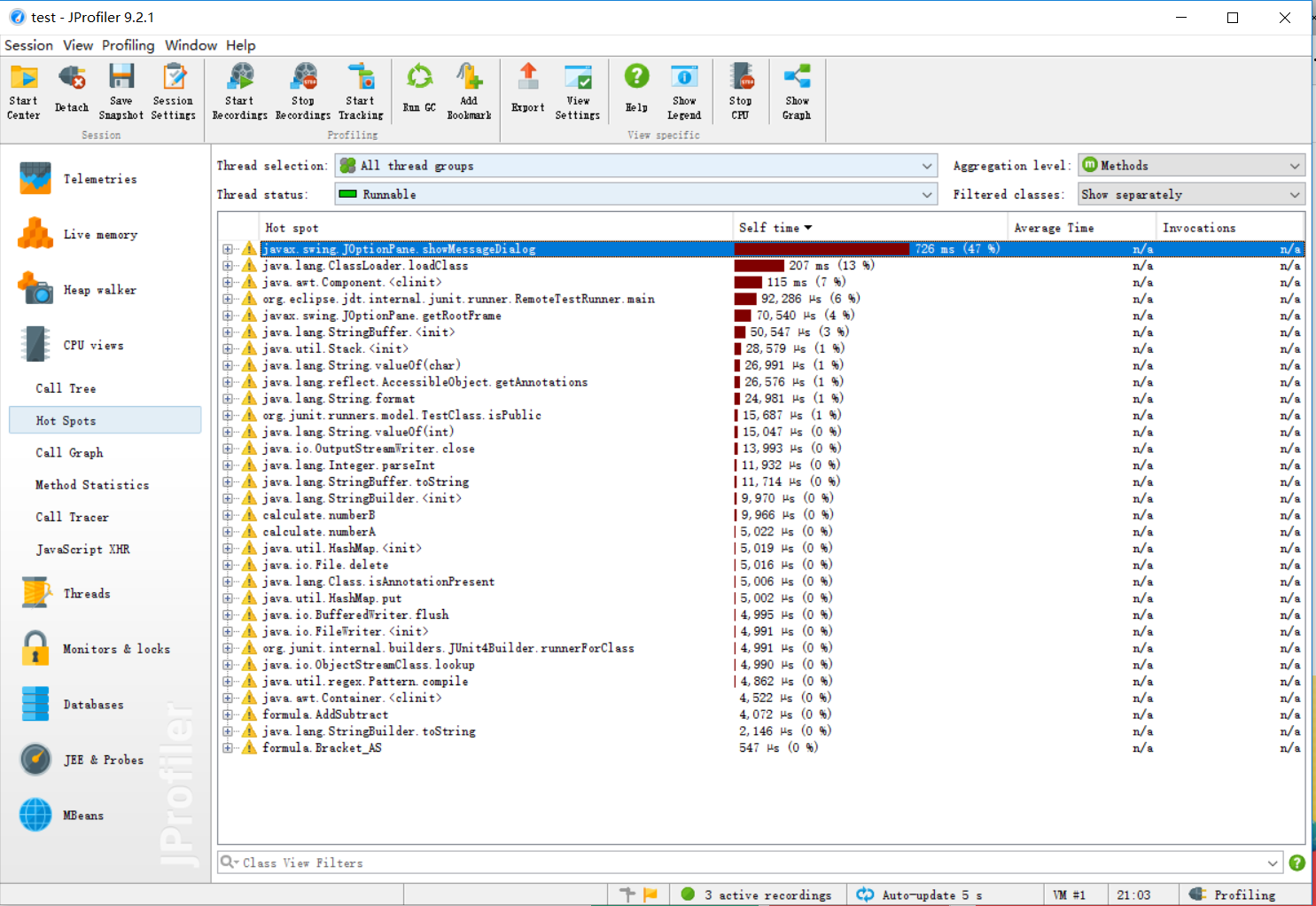


六、计算模块部分单元测试展示

@Test public void testWork() { assertEquals(0, stack.work("7-5÷(1*37)÷(1*83)", 1, 900, 1)); assertEquals(30, stack.work("55+(-25)÷5*(20-15)", 2, 300, 1)); assertEquals(80, stack.work("((55+25)÷5)*(20-15)", 2, 300, 1)); assertEquals(0, stack.work("60*(20-15)", 2, 200, 1)); }
该部分测试的是栈的运算。
第一个断言测试的是无法整除返回错误标志0;
第二个断言测试的是负数运算;
第三个断言测试的是特殊括号位置的运算;
第四个断言测试的是超过数值返回错误标志0。
@Test public void testAll() { // 顺序不同以及异常测试。生成的文件会被覆盖。 String[] arg0 = new String[] { "-n", "100", "-m", "5", "100", "-o", "3", "-c", "-b" }; String[] arg1 = new String[] { "-m", "5", "50", "-o", "3", "-n", "100", "-c" }; String[] arg2 = new String[] { "-o", "3", "-m", "5", "50", "-n", "100", "-b" }; String[] arg3 = new String[] { "-n", "100", "-o", "3", "-m", "5", "50" }; Command.main(arg0);// 有括号四则运算测试 Command.main(arg1);// 四则运算测试 Command.main(arg2);// 有括号加减运算测试 Command.main(arg3);// 加减运算测试 }
该部分测试的命令行的更改输入顺序的四种出题选择正常运行。输入异常部分请看第七点。
@Test public void testDecide2() { int[] find = new int[2]; find = calculate.decide2(20, 2); assertEquals(2, find[1]); find = calculate.decide2(13, 2); assertEquals(1, find[0]); } decide2(int x, int min)为除法选择除数的函数,函数如下: // 被除数能被除数整除并不低于最小 public static int[] decide2(int x, int min) { int[] judge = new int[] { 1, 0 }; int temp = Math.abs(x) / min - min + 1;// 除数的范围 for (int i = min; i < (temp + min); i++) { if (Math.abs(x) % i == 0) {// 判断是否整除 judge[0] = 0; judge[1] = i; return judge; } } return judge; }
其中,judge[0]用于判断该数能否有可整除的除数,1为没有,0为有,judge[1]为除数的值。该单元测试则测试了一次可产生除数与一次不能产生除数的情况。
七、计算模块部分异常处理说明
@Test public void testAll() { String[] arg4 = new String[] { "-o", "3", "-m", "5", "50", "-n" }; String[] arg4_1 = new String[] { "-o", "3", "-n", "-m", "5", "50" }; String[] arg4_2 = new String[] { "-n", "100000", "-m", "5", "50" }; String[] arg4_3 = new String[] { "-o", "3", "-m", "5", "50" }; String[] arg5 = new String[] { "-n", "50" }; String[] arg5_1 = new String[] { "-m", "5", "-n", "50", "-o", "3" }; String[] arg5_2 = new String[] { "-n", "50", "-m", "3" }; String[] arg5_3 = new String[] { "-n", "50", "-o", "3", "-m" }; String[] arg5_4 = new String[] { "-m", "-n", "50" }; String[] arg6 = new String[] { "-o", "11", "-m", "5", "50", "-n", "100" }; String[] arg6_1 = new String[] { "-n", "100", "-o", "-m", "5", "50" }; String[] arg6_2 = new String[] { "-n", "100", "-m", "5", "50", "-o" }; String[] arg7 = new String[] { "-m", "5", "20", "-n", "100", "-c" }; String[] arg7_1 = new String[] { "-m", "5", "50", "-n", "100", "-b" }; String[] arg8 = new String[] { "-b", "1", "-o", "3", "-m", "5", "50", "-n", "100" }; String[] arg8_1 = new String[] { "-c", "1", "-o", "3", "-m", "5", "50", "-n", "100" }; String[] arg8_2 = new String[] { "-n", "100", "-m", "5", "50", "-d" };
Command.main(arg4);// 缺少题数值测试 Command.main(arg4_1); Command.main(arg4_2);// 题数值过大测试 Command.main(arg4_3);// 缺少题数测试 Command.main(arg5);// 缺少数值范围 Command.main(arg5_1);// 缺少数值范围上限测试 Command.main(arg5_2); Command.main(arg5_3);// 缺少数值范围上下限测试 Command.main(arg5_4); Command.main(arg6);// 操作符数值过大测试 Command.main(arg6_1);// 缺少操作符数值测试 Command.main(arg6_2); Command.main(arg7);// 乘除需要上界大于下界的平方 Command.main(arg7_1);// 括号需要操作符数大于1 Command.main(arg8);// 输入非法测试之b后有数字 Command.main(arg8_1);// 输入非法测试之c后有数字 Command.main(arg8_2);// 输入非法测试之无辨识字符 }
- 缺少题数值(-n后无带数字,如arg4与arg4_1)时,提醒缺少题数值,并告知-n的范围;
- 题数值过大(-n后数值超过10000,如arg4_2)时,提醒告知题数值范围(过小同理);
- 缺少题数(命令中无-n,如arg4_3)时,提醒-n为必须项,并告知-n范围。
- 缺少数值范围(命令中无-m,如arg5)时,提醒-m为必须项,并告知-m上下限各自范围;
- 缺少数值范围上限(-m后只带一个数字,如arg5_1和 arg5_2)时,提醒缺少上限,并告知上限范围;
- 缺少数值范围上下限(-m后不带数字,如arg5_3和 arg5_4)时,提醒缺少上下限,并告知上下限各自范围。
- 操作符数值过大(-o后数值超过10,如arg6)时,提醒告知操作符数值范围(过小同理);
- 缺少操作符数值(输入-o,后方没有带数值,如arg6_1与arg6_2)时,提醒缺少操作符数值,并告知-o范围。
- 选择乘除法但是上界小于下界的平方,无法生成含有乘除的式子(如arg7)时,提醒上界需大于下界的平方;
- 选择括号但是操作符默认为1或选择为1,不符合生成括号的条件(如arg7_1)时,提醒选择括号需要操作符数大于1。
- –b(或-c)后带数字(如arg8与arg8_1),提醒-b(或-c)后不能带数字;
- 出现除m、n、o、b、c外的字符如d等(如arg8_2),提醒输入值非法
八、界面模块的详细设计过程
1、初始设计
初始界面出题做题单选,出题界面选择需求,做题界面先输入用户名将题目一行一行读出,填入答案后才可以跳转下一题,最后给出做题情况以及该用户的历史得分
2、设计框图

3、具体实现
1、出题做题选择界面
2、选择出题界面
选中特定框时有提示输入要求
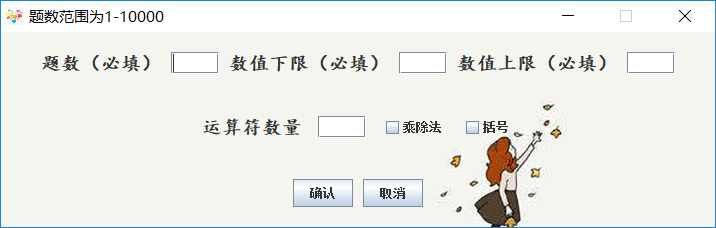
3、出题成果

4、做题用户名界面
5、选择题目文件界面,限制txt文件

6、题目上传成功并开始计时页面
7、做题界面

8、用户第一次做题界面

9、用户再次做题界面
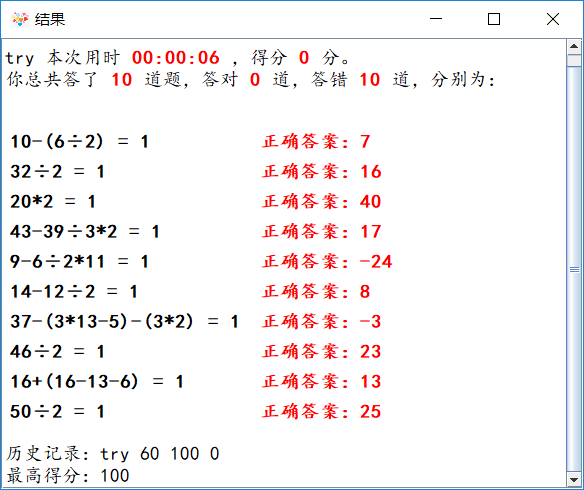
九、界面模块与计算模块的对接
1、对接项
(1)出题模式
获取参数后调用类出题创建文件
(2)做题模式
获取用户姓名后,执行上传文件类,读取后进行做题操作输出结果
2、流程图

十、结对过程的描述
1、描述
我们两个人在结对过程中不断切换驾驶员领航员角色,对不同的性能需求进行分板块进行,比较顺利的完成了不同板块的对接与项目的测试。完成了整个项目的性能分析和单元测试的覆盖率分析。
2、结对照片展示

十一、结对编程的优缺点
1、结对编程优缺点
(1)优点
互相帮助、互相学习、能力上得到互补
可以增强代码和产品质量,有效地减少bug
在编程中,相互讨论,可能更快有效地解决问题
有两台电脑可以测试程序效果
(2)缺点:
对于有不同习惯的编程人员,可能在一起工作会产生一些麻烦,甚至矛盾。
结对编程可能让程序员们相互学习得更快,但有些时候可能会滋生不良氛围
有经验的人可能更喜欢单独作业,结对会使他的状态受到影响
2、结对个人优缺点
庄莉
优点:
认真细心,有责任心
代码能力高
动手能力强
缺点:
有时候对于小问题过于钻牛角尖
王璐瑶:
优点:
对字符串以及字符串数组的处理十分熟练
任劳任怨
很有想法,有好点子
缺点:
缺点:因生病而不在状态,没注意到比较细的地方,时间较少
十二、完成后实际的PSP
|
PSP |
任务内容 |
实际完成需要的时间(min) |
|
Planning |
计划 |
0.5 |
|
Estimate |
估计这个任务需要多少时间,并规划大致工作步骤 |
0.5 |
|
Development |
开发 |
53.25 |
|
Analysis |
需求分析 (包括学习新技术) |
0.5 |
|
Design Spec |
生成设计文档 |
0.25 |
|
Design Review |
设计复审 (和同事审核设计文档) |
0.25 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
0.25 |
|
Design |
具体设计 |
1 |
|
Coding |
具体编码 |
40 |
|
Code Review |
代码复审 |
1 |
|
Test |
测试(自我测试,修改代码,提交修改) |
10 |
|
Reporting |
报告 |
8 |
|
Test Report |
测试报告 |
7 |
|
Size Measurement |
计算工作量 |
0.5 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
0.5 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号