线性回归——梯度下降法
前面的文章讲了使用最小二乘法来求线性回归损失函数的最优解,最小二乘法为直接对梯度求导找出极值,为非迭代法;而本篇文章了使用一个新的方法来求损失函数的极值:梯度下降法(Gradient Descendent, GD),梯度下降法为最优化算法通常用于求解函数的极值,梯度下降法为迭代法,给定一个β在梯度下降最快方向调整β,经过N次迭代后找到极值,也就是局部最小值或全局最小值;
梯度下降法又分为批量梯度下降法与随机梯度下降法,通常随机梯度下降法性能会好点;不过我们这里讲的为批量梯度下降法;
梯度
梯度为微积分中的概念,梯度所指方向为方向导数最大的量,梯度指出了全局或局部范围内哪个方向函数增长最快,可用于求函数极大值或极小值;
梯度求法为:对函数每个自变量求偏导数,将该偏导数作为其自变量方向的坐标;
▽表示梯度
例如: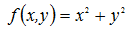 的梯度为:
的梯度为:
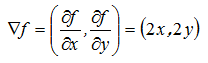
梯度下降法
下面先通过一个简单的示例来了解梯度下降法的使用,我们使用梯度下降法来求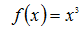
的极小值:
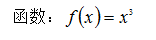
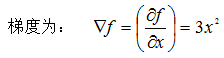
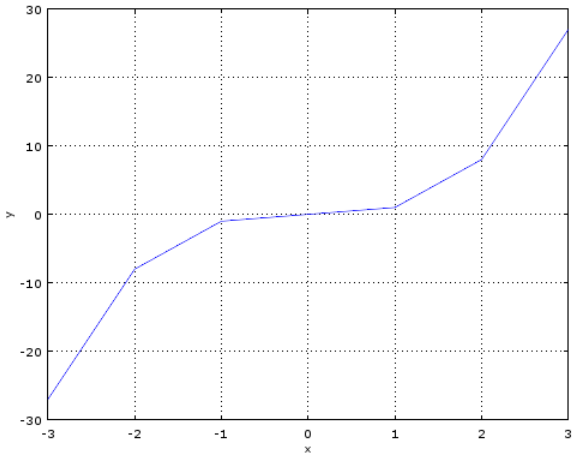
函数的图形
当X=3为时f(x)=27,关于X的偏导数值为27也就是梯度为27;当X沿着+27方向变化f(X)将会增大,如X沿着相反方向也就是-27方向变化f(X)值将会减小,即增大时为梯度上升,减少为梯度下降;我们可以通过这种方式来求f(X)的极小值与极大值,求极小值的方法也称为梯度下降法;
已上述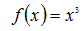 为例,使用梯度下降法求极小值;选择一个自变量初始点(种子点),计算该梯度值,然后自变量沿着梯度相反方向下降(负方向),下降步长通常根据经验值指定,用α表示;通过以下几点来判断是否已经找到极小值:
为例,使用梯度下降法求极小值;选择一个自变量初始点(种子点),计算该梯度值,然后自变量沿着梯度相反方向下降(负方向),下降步长通常根据经验值指定,用α表示;通过以下几点来判断是否已经找到极小值:
1、达到指定迭代次数
2、当前的函数值大于上次函数值
3、函数值非常接近于0
 梯度为
梯度为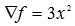 ,初始点选择3,步长设置为:0.1
,初始点选择3,步长设置为:0.1
迭代方式为: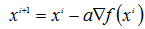 ,i为迭代的次数;
,i为迭代的次数;
迭代过程:
x = 3,梯度为:27,降下方向为-27方向
x = 3-0.1*27=0.3,梯度为:3*0.3^2=0.27
x = 0.3-0.1*0.27=0.273,梯度为:3*0.273^2=0.223587
x = 0.273-0.1*0.223587= 0.2506413,梯度为:3*0.2506413^2=0.18846318379707
x = 0.2506413-0.1*0.18846318= 0.23179498,梯度为:3*0.231794982^2=0.1611867410
迭代了五次,假设最大迭代次数为5,已经求出极小值;为当x=0.23179498时,函数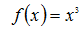
的极小值为:0.01245409225705;
线性回归
上篇文章中说过,拟合函数为: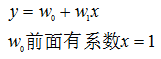 线性回归的损失函数为:
线性回归的损失函数为:
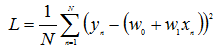

损失函数关于W的偏导数为:

则有:
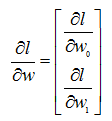
N为数据集的大小,w , x , y 为向量;

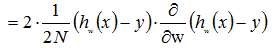
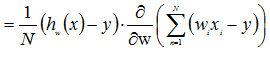

w向量中每个标量的偏导数为:
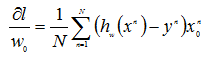
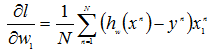
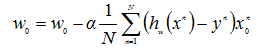
设α为步长,求w的迭代公式为:
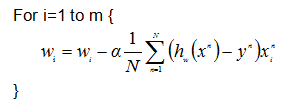
参考资料:
http://zh.wikipedia.org/wiki/梯度
a first course in machine learning


 浙公网安备 33010602011771号
浙公网安备 33010602011771号