线性回归——最小二乘法_实例（二）
上篇文章介绍了最小二乘法矩阵形式的理论与证明、计算过程，这里使用程序代码的方式计算出矩阵形式的解，并给出线性拟合；
Octave代码
clear all;close all;
% 拟合的数据集
x = [1,2;1,6;1,9;1,13];
y = [4;8;12;21];
% 根据公式 w = (x'*x)^-1 * x' * y
% 与上篇文章一样一步步分解如下，其实这里可以不用分解，上篇文章分解时为了好计算
x_t =x'*x;
%% (x'*x)^-1或inv(x' * x)
x_i = x_t^-1;
x_i_t = x_i*x';
% 求出w
w = x_i_t * y;
%% 在画板上绘制出数据集的点
figure(1);hold off
plot(x(:,2),y,'bo','markersize',5,'linewidth',2)
set(gca,'xtick',0:1:25)
% 画布大小为25*25
xplot = [0 25];
yplot = [0 25];
xlim(xplot)
ylim(yplot)
hold on
% 打印出拟合的线段
plot(xplot,w(1,:)+w(2,:)*xplot,'r','linewidth',2)
set(gca,'yTick',1:1:25)
set(gca,'xTick',1:1:25)
xlabel('x');
ylabel('y');
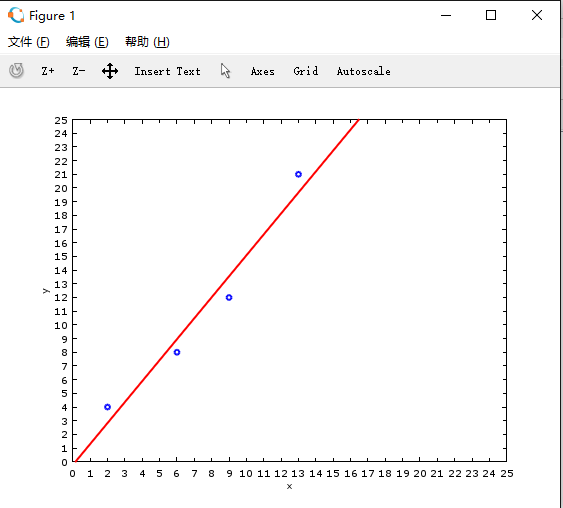
运行结果
