单目标问题的烟花优化算法求解matlab仿真,对比PSO和GA

1.程序功能描述
单目标问题的FW烟花优化算法求解matlab仿真,对比PSO和GA。最后将FW，GA，PSO三种优化算法的优化收敛曲线进行对比。

2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

 

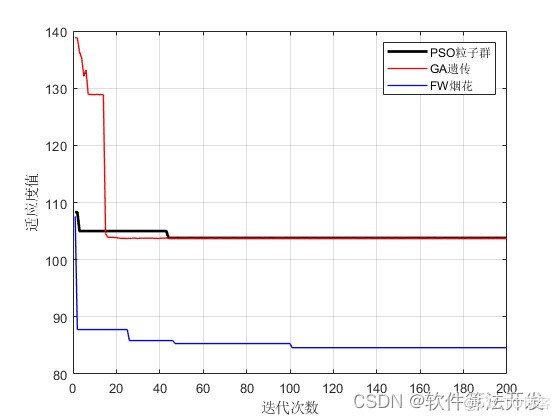
3.核心程序

for t=1:Iter
    %计算每个烟花适应度值
    for i=1:Npop
        yfit(i)=func_fitness(x(i,:));
    end
    [F(t),~]=min(yfit);
    Fmin=min(yfit);% 当前代最小适应度
    Fmax=max(yfit);% 当前代最大适应度
    %计算每个烟花的爆炸半径E_R和爆炸数目E_N以及产生的爆炸火花
    E_R = zeros(1,Npop);
    E_N = zeros(1,Npop);
    % 高斯变异火花产生
    Mut=randperm(Npop); % 随机选取烟花索引
    for m1=1:M   % 对M个烟花进行变异
        m=Mut(m1);            % 随机选取烟花
        for n=1:E_N(m)
            e=1+sqrt(1)*randn(1,Dim); % 高斯变异因子
            sparks(n,:,m)=sparks(n,:,m).*e;% 应用变异
            % 变异后的位置约束 
            if sparks(n,1,m)>500||sparks(n,1,m)<100
               sparks(n,1,m)=unifrnd(100,500,1,1); 
            end
            if sparks(n,2,m)>79||sparks(n,2,m)<69
               sparks(n,2,m)= unifrnd(69,79,1,1);
            end
        end
    end
    [Fitness,X]=sort(Fitness);  % 适应度升序排列
    x(1,:)=E_Sum(X(1),:);    % 最优个体
    dist=pdist(E_Sum);       % 求解各火花两两间的欧式距离
    S=squareform(dist);      % 将距离向量重排成n*n数组
    P = zeros(1,n);
    for i=1:n                % 分别求各行之和
        P(i)=sum(S(i,:));
    end
end
 
 
%求最大值输出
[F(Iter),Y]=min(Fit2);
 
 
figure;
plot(F, 'LineWidth', 2)
xlabel('迭代次数')
ylabel('目标函数值')
title('FWA算法迭代曲线');
 
save R3.mat  F
48

　　

4.本算法原理
烟花优化算法是一种模拟自然界烟花爆炸现象的启发式算法，由烟花发射、爆炸、再次爆炸和再次发射四个阶段组成。该算法通过模拟烟花在夜空中爆炸的过程，探索搜索空间，寻找全局最优解。

 

适应性与灵活性：FWA通过模拟烟花爆炸的动态过程，提供了搜索空间的多样性，适合解决复杂、非线性问题；PSO通过粒子的速度和位置更新快速接近最优解，适合快速收敛的问题；GA通过模拟生物进化机制，具有较强的全局搜索能力，适用于解空间较大的问题。
参数调整：FWA的爆炸半径和火花数直接影响搜索效率和精度，需仔细调整；PSO的惯性权重w、加速常数c1​,c2​对算法性能影响显著；GA的选择压力、交叉概率和变异概率是关键参数，需根据问题特性仔细设定。
收敛性和稳定性：FWA在后期迭代中可能因火花过度密集而降低搜索效率；PSO易陷入局部最优，特别是在高维问题中；GA的收敛速度较慢，但通常能获得较好的全局解。