通过matlab分别对比PSO,反向学习PSO,多策略改进反向学习PSO三种优化算法

1.程序功能描述
分别对比PSO,反向学习PSO,多策略改进反向学习PSO三种优化算法.对比其优化收敛曲线。

2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

 

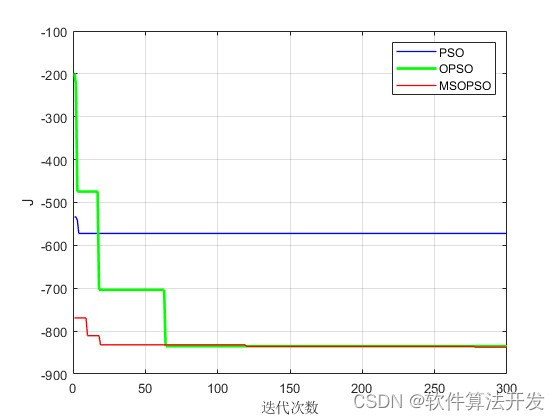
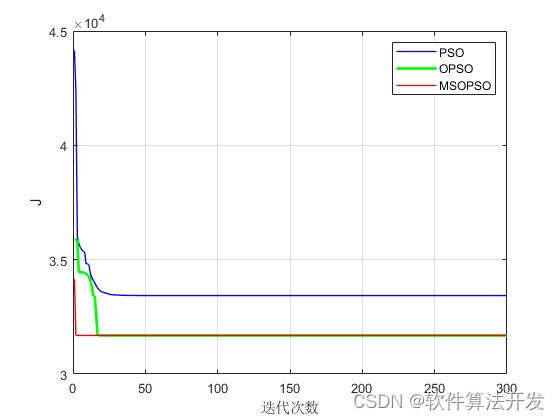
3.核心程序

 

for t=1:tmax
    t
    time(t) = t;
    w       = 0.5;
    for i=1:Pop
        if t > 1
            %N
            x(1,i)         = x_(1,i);
            x_best(1,i)    = x_best_(1,i);
            %I
            y(1,i)         = y_(1,i);
            y_best(1,i)    = y_best_(1,i);
        end
        %N
        %速度1设置
        va(1,i) = w*va(1,i) + c1*rand(1)*(x_best(1,i)-x(1,i)) + c2*rand(1)*(Tx_best-x(1,i));
        %更新
        x(1,i)  = x(1,i) + va(1,i);
        %变量1的限制
        if x(1,i) >= max1
           x(1,i) = max1;
        end
        if x(1,i) <= min1
           x(1,i) = min1;
        end                             
 
        %I
        %速度2设置
        vb(1,i) = w*vb(1,i) + c1*rand(1)*(y_best(1,i)-y(1,i)) + c2*rand(1)*(Ty_best-y(1,i));
        %更新
        y(1,i)  = y(1,i) + vb(1,i);
        %变量2的限制
        if y(1,i) >= max2
           y(1,i) = max2;
        end
        if y(1,i) <= min2
           y(1,i) = min2;
        end                            
 
       [BsJ,x(1,i),y(1,i)] = func_fitness(x(1,i),y(1,i));  
        
        if BsJ<BsJi(i)
           BsJi(i)        = BsJ;
           x_best(1,i)    = x(1,i);
           y_best(1,i)    = y(1,i);
        end
        if BsJi(i)<minJi
           minJi      = BsJi(i);
           Tx_best    = x(1,i);
           Ty_best    = y(1,i);
        end
        %反向
        %反向学习
        %N
        x_(1,i)         = (max1+min1)-x(1,i);
        x_best_(1,i)    = (max1+min1)-x_best(1,i);
        %I
        y_(1,i)         = (max2+min2)-y(1,i);
        y_best_(1,i)    = (max2+min2)-y_best(1,i);
 
       [BsJ,x(1,i),y(1,i)] = func_fitness(x_(1,i),y_(1,i));
 
        if BsJ<BsJi(i)
           BsJi(i)        = BsJ;
           x_best(1,i)    = x_(1,i);
           y_best(1,i)    = y_(1,i);
        end
        if BsJi(i)<minJi
           minJi      = BsJi(i);
           Tx_best    = x_(1,i);
           Ty_best    = y_(1,i);
        end
    end
    Jibest(t) = minJi;
end
Tx_best
Ty_best
figure;
plot(Jibest,'b','linewidth',1);
xlabel('迭代次数');
ylabel('J');
grid on
 
save R2.mat Jibest

　　

4.本算法原理
4.1 粒子群优化算法 (PSO)
粒子群优化算法模拟鸟群或鱼群的社会行为，通过迭代搜索最优解。在n维搜索空间中，每一个粒子代表一个潜在解，并具有速度和位置属性。在每次迭代过程中，粒子根据自身的历史最优位置（个体极值pi​）和全局最优位置（全局极值g）更新自己的速度和位置。

4.2 反向学习粒子群优化算法 (OPSO)
反向学习PSO是在传统PSO基础上引入了反向学习机制，当搜索过程陷入局部最优时，通过回溯过去的最优解来调整粒子的速度和方向，从而增加跳出局部最优的可能性。

改进要点： RL-PSO会在适当的时候启用反向学习阶段，此时速度更新会参考历史最优位置而非当前最优位置，具体数学表达式因不同实现方式而异，但一般包含对过去优良解的记忆和利用。

4.3 多策略改进反向学习粒子群优化算法 (MSO-PSO)
MSO-PSO融合了多种策略并结合反向学习的思想，进一步增强算法的全局搜索能力和收敛速度。例如，可能结合自适应权重调整、动态邻域搜索、精英保留策略等。