基于免疫算法的TSP问题求解matlab仿真

1.程序功能描述
旅行商问题（Travelling Salesman Problem, TSP）是一个经典的组合优化问题，其目标是在给定一组城市及其相互之间的距离情况下，寻找一条经过每个城市恰好一次且返回起点的最短回路。TSP因其NP完全性及广泛应用背景而备受关注。免疫算法（Immune Algorithm, IA），作为一种受生物免疫系统启发的演化计算方法，近年来被广泛应用于解决此类复杂优化问题。

2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

 

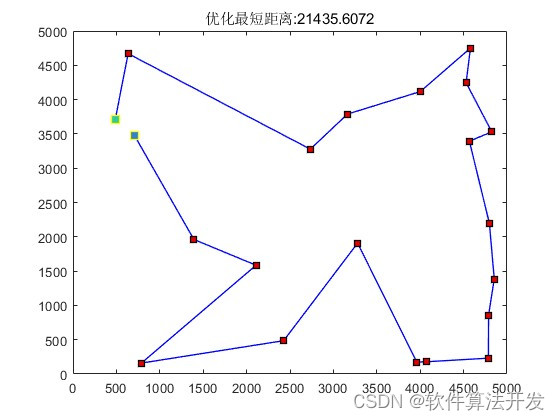
3.核心程序

 

%循环迭代 
% 输出最优解
%最优变量
ybest = ysort(:,1);   
%最优值
Lbest = trace(end);  
 
% 绘制最优路径图
figure
 
for i=1:Num-1
    plot([city(ybest(i),1),city(ybest(i+1),1)],[city(ybest(i),2),city(ybest(i+1),2)],'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
    hold on;
end
plot([city(ybest(1),1)],[city(ybest(1),2)],'rs',...
'LineWidth',1,...
'MarkerSize',8,...
'MarkerEdgeColor','y',...
'MarkerFaceColor',[0.2,0.5,0.8]);
hold on;
plot([city(ybest(end),1)],[city(ybest(end),2)],'ks',...
'LineWidth',1,...
'MarkerSize',8,...
'MarkerEdgeColor','y',...
'MarkerFaceColor',[0.2,0.8,0.6]);
hold on;
title(['优化最短距离:',num2str(Lbest)]);
 
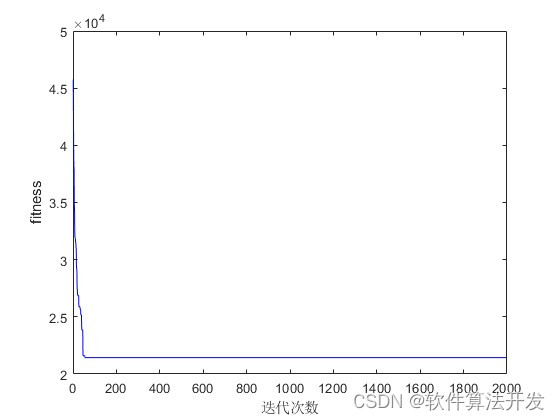
% 绘制迭代过程中最优路径长度随迭代次数的变化曲线
figure
plot(trace,'b-');
xlabel('迭代次数')
ylabel('fitness')

　　

4.本算法原理
4.1免疫算法概述
免疫算法模拟了生物免疫系统的运作机制，主要包括以下几个核心概念：

抗原（Antigen）：在TSP中，抗原可以对应于待优化问题的解，如一条候选的城市访问路径。

抗体（Antibody）：抗体是免疫系统针对特定抗原产生的识别与反应单元。在IA中，抗体表示为问题的可能解，即一条城市访问序列。抗体通常具有编码结构，以便于遗传操作和适应度评估。

免疫库（Repertoire）：免疫库是存储抗体的集合，相当于演化算法中的种群。在TSP应用中，免疫库包含若干个不同的城市访问路径。

克隆选择（Clonal Selection）：这是免疫系统的核心机制，通过复制高亲和力（适应度）的抗体来增强其在免疫库中的比例。在IA中，对应于选择优秀的抗体个体进行复制（克隆），以保持或增加它们在种群中的数量。

变异（Mutation）：生物免疫系统中，抗体在克隆过程中会发生随机变异以增加多样性。在IA中，通过引入变异算子（如交换、逆序等）对克隆的抗体进行局部调整，生成新的解变种。

免疫记忆（Immune Memory）：免疫系统能够记住先前遇到的抗原，以便快速响应再次出现的威胁。在IA中，这体现在保留历史最优解或精英个体，确保算法不会遗忘已发现的好解。

4.2免疫算法应用于TSP
将免疫算法应用于TSP求解时，关键步骤包括：

初始化：随机生成一个包含Npop个抗体（即城市访问序列）的免疫库，每个抗体由Num个整数构成，表示城市编号，且无重复。

适应度评估：对于每个抗体A_i，计算其对应的路径长度L(A_i)，作为其适应度f(A_i)。在TSP中，适应度函数通常取反路径长度，即f(A_i) = 1 / L(A_i)，以使优化目标与最大化适应度一致。路径长度L(A_i)通过以下公式计算：

 

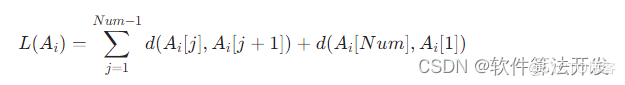
其中，d(u, v)表示城市u和城市v之间的距离，从距离矩阵dist中获取。

克隆选择与变异：选择适应度较高的抗体进行克隆，然后对克隆体进行变异操作。变异可采用以下两种策略之一：

 

免疫记忆：记录当前迭代周期内找到的最优抗体A_best及其适应度f(A_best)。在后续迭代中，即使A_best未被选中进行克隆，也应将其保留在种群中。

迭代终止条件：当达到预设的最大迭代次数Niter或适应度改善阈值时，终止算法，并返回当前最优抗体A_best作为TSP问题的近似最优解。