树状数组之图腾计数
题目

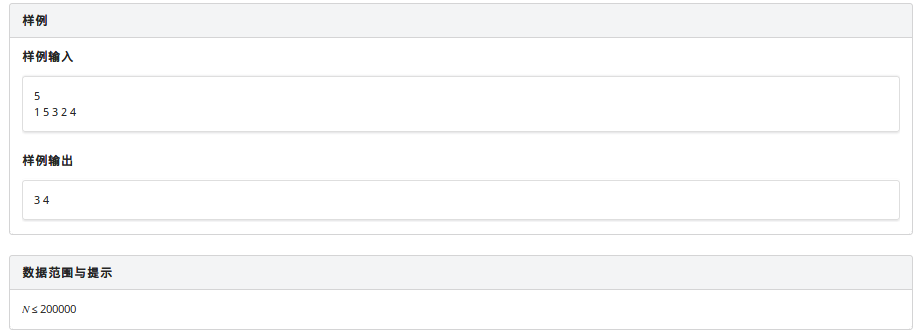
思路
开始码了遍暴力
#include<bits/stdc++.h>
using namespace std;
int a[200000+10];
int cnt1,cnt2;
int main(){
int n;scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
if(n<3){
printf("0\n");
printf("0\n");
return 0;
}
for(int i=1;i<=n-2;i++){
for(int j=i+1;j<=n-1;j++){
for(int k=j+1;k<=n;k++){
if(a[i]<a[j]&&a[k]<a[j])cnt2++;
if(a[i]>a[j]&&a[k]>a[j])cnt1++;
}
}
}
printf("%d ",cnt1);
printf("%d\n",cnt2);
return 0;
}
不用想肯定是错的,所以就去想其他思路
- 对于某一个柱子,可以求它左右延伸的距离
于是我想到了单调栈,和-->这道题,不过显然这样是不对的,经过一番折腾后,get到了如下思路
- 对于某一个柱子,维护其左右两边比其矮的个数,左右相乘为以该柱子为中心上凸的情况数
- 对于某一个柱子,维护其左右两边比其高的个数,左右相乘为以该柱子为中心下凸的情况数
那么怎么维护呢?我想到了树状数组求逆序对,和-->某道题有一丝丝像。
以上凸情况为例
- -->维护p数组存放高度i对应的位置,因为高度是不重复的
- -->维护树状数组以位置为下标,表示该位置下的柱子是否存在(方便查询个数)
- -->对高度从小到大循环,确保在当前柱子放之前,比其小的柱子已经放完
- -->查询其左右两边的柱子个数(一定是比当前柱子小的,因为大的还没放)
- -->将当前柱子放入相应位置
for(int i=1;i<=n;i++){
long long l=ask(p[i]-1);
long long r=ask(n)-ask(p[i]);
ans1+=l*r;
add(p[i],1);
}
下凸情况反过来跑一遍就行(记得清空树状数组)
总代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=200000+10;
long long a[maxn],c[maxn],p[maxn];
long long n;
inline long long read(){
long long s=0;
char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&& ch<='9')s=(s<<3)+(s<<1)+(ch^48),ch=getchar();
return s;
}
void add(int x,int y){
for(;x<=n;x+=x&-x)c[x]+=y;
}
int ask(int x){
int ans=0;
for(;x;x-=x&-x)ans+=c[x];
return ans;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
p[a[i]]=i;
}
if(n<3){
printf("0\n");
printf("0\n");
return 0;
}
long long ans1=0,ans2=0;
for(int i=1;i<=n;i++){
long long l=ask(p[i]-1);
long long r=ask(n)-ask(p[i]);
ans1+=l*r;
add(p[i],1);
}
memset(c,0,sizeof(c));
for(int i=n;i>=1;i--){
long long l=(long long)ask(p[i]-1);
long long r=(long long)(ask(n)-ask(p[i]));
ans2+=l*r;
add(p[i],1);
}
printf("%lld %lld\n",ans2,ans1);
return 0;
}

