图论最短路之分层图

一般问题

在图上，将某一条边或多条边进行修改，进而求最短路

变形

包括删去某一（或多条）条边（权值变为0），将某一条边（或多条）减半，将某一条边进行特殊赋值，求最短路

通用解法

对于k次修改，我们将整张图复制k次（一般点数和边数都较小），在单独的每层图中，边权都与原图相同，不同的是，我们将上下两层连接起来
如图（图片来自洛谷https://www.luogu.com.cn/blog/xiaohou/fen-ceng-tu）

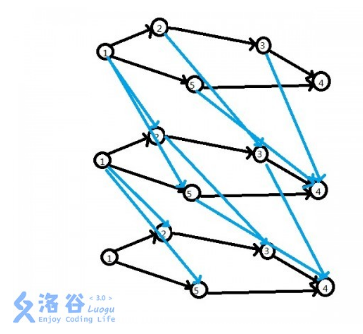
这张图中将一张图复制了两次，即可理解为两次改变权值，假设我们对图的修改为将某边修改为0，一张有向图中，那么对于同一层的\(<u_i,v_i>\)其长度等于\(<u_{i-1},v_{i-1}>\)的长度，但是\(<u_{i-1},v_i>\)长度设为0即可，最后根据建出来的图跑一遍最短路即可

一道裸题

[BJWC2012]冻结

题目大意

将k条边变为原来1/2，求最短路

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int tot=0;
int head[maxn],ver[maxn],next[maxn],dis[maxn];
void add(int x,int y,int z){
	ver[++tot]=y,dis[tot]=z,next[tot]=head[x],head[x]=tot;
}
int n,m,k;
priority_queue<pair<int,int> >q;
bool v[maxn];
int d[maxn];
void dij(int s){
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()){
		int x=q.top().second;
		q.pop();
		if(v[x])continue;
		v[x]=1;
		for(int i=head[x];i;i=next[i]){
			int y=ver[i],z=dis[i];
			if(d[y]>d[x]+z){
				d[y]=d[x]+z;
				q.push(make_pair(-d[y],y));
			}	
		}
	}
}

main(){
	scanf("%d%d%d",&n,&m,&k);
	int u,v;int dd;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&dd);
		add(u,v,dd);
		add(v,u,dd);
		for(int j=1;j<=k;j++){
			add(u+j*n,v+j*n,dd);
			add(v+j*n,u+j*n,dd);
			add(u+j*n-n,v+j*n,dd/2);
			add(v+j*n-n,u+j*n,dd/2);
		}
		
	}
	
	dij(1);
	for (int i = 1; i <= k; i++)
		d[n] = min(d[n], d[n+n*i]);
	printf("%d\n", d[n]);
}