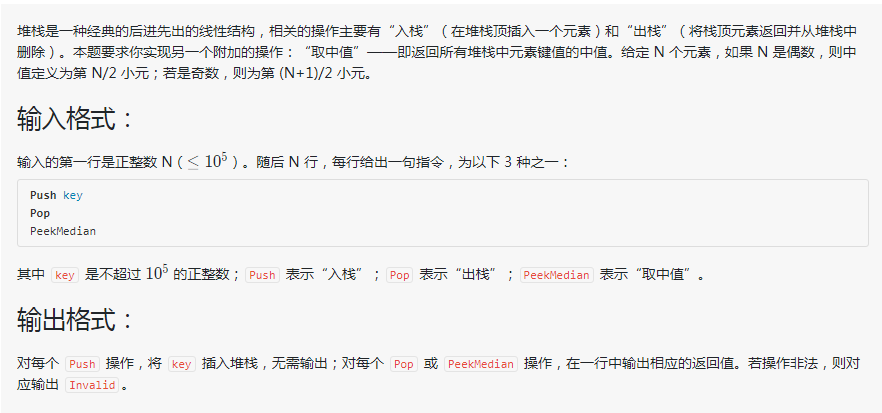
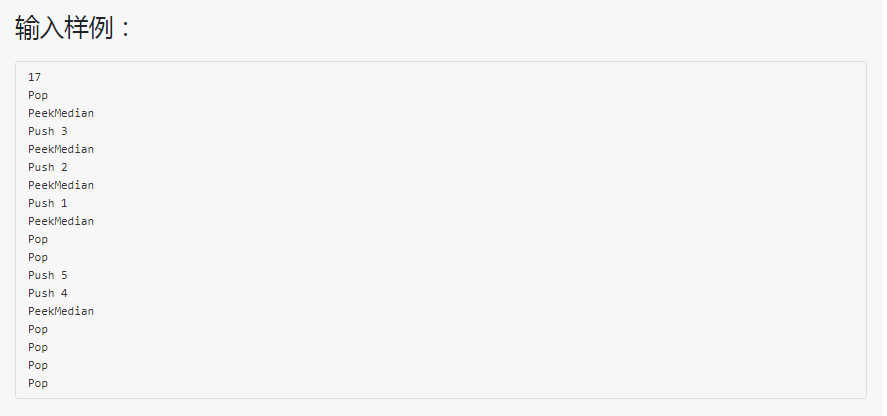
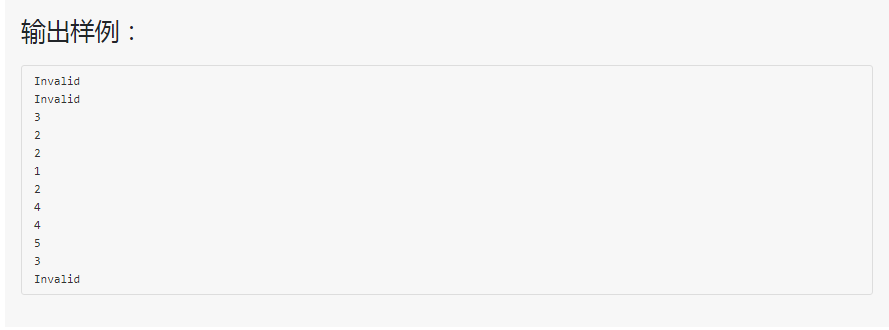
进阶实验8-2.2 特殊堆栈 (30分)-栈+树状数组+二分法

 

 

 

 解题思路：

尝试用堆排，发现超时

后在网上学习到树状数组的方法，终AC

推荐容易树状数组的一篇大牛blog https://www.cnblogs.com/hsd-/p/6139376.html

树状数组的查询和修改的复杂度均为log(n)

 

#include <stdio.h>
#include <malloc.h>
#include <string.h>
#define Max 100000
int tree[Max]={0};//存储叶子结点，叶子结点值为0表示不存在堆栈，值为1表示在堆栈中有1个，值为2表示在堆栈中有2个，以此类推
int n;
int cnt=0;
typedef struct {
    int *Data;
    int Top;
    int MaxSize;
}*Stack;
Stack CreateStack(int size) {
    Stack S=(Stack)malloc(sizeof(Stack));
    S->Data=(int *)malloc(sizeof(int)*size);
    S->MaxSize=size;
    S->Top=-1;
    return S;
}
int IsEmpty(Stack S) {
    if(S->Top==-1)
        return 1;
    return 0;
}
int IsFull(Stack S) {
    if(S->Top==S->MaxSize-1)
        return 1;
    return 0;
}
int Pop(Stack S) {
    if(IsEmpty(S))
        return -1;
    return S->Data[S->Top--];
}
int Push(Stack S,int x) {
    if(IsFull(S))
        return 0;
    S->Data[++S->Top]=x;
    return 1;
}
//求二进制x最低位1，如lowbit(6)=2;(0110)&&(1010)=2
int lowbit(int x) {
    return x&(-x);
}
//获得在x之前的个数
int getsum(int x) {
    int i;
    int sum=0;
    for(i=x; i>0; i-=lowbit(i))
        sum+=tree[i];
    return sum;
}
void add(int x,int y) {
    int i;
    for(i=x; i<Max; i+=lowbit(i)) {
        tree[i]+=y;
    }
}
void PeekMedian() {
    int left=1,right=Max,k=(cnt+1)>>1;
    while(left<right) {
        int mid=(left+right)>>1;
        if(getsum(mid)>=k)
            right=mid;
        else
            left=mid+1;
        
    }
    printf("%d\n",left);
}
int main() {
    
    scanf("%d",&n);
    Stack S=CreateStack(n);
    char c[11];
    int i;
    for(i=0; i<n; i++) {
        scanf("%s",c);
        if(c[1]=='o') {
            if(IsEmpty(S))
                printf("Invalid\n");
            else {
                int tmp=Pop(S);
                printf("%d\n",tmp);
                add(tmp,-1);
                cnt--;
            }
        } else if(c[1]=='u') {
            int x;
            scanf("%d",&x);
            Push(S,x);
            add(x,1);
            cnt++;
        } else {
            if(IsEmpty(S))
                printf("Invalid\n");
            else {
                PeekMedian();
            }
        }
    }
    return 0;
}