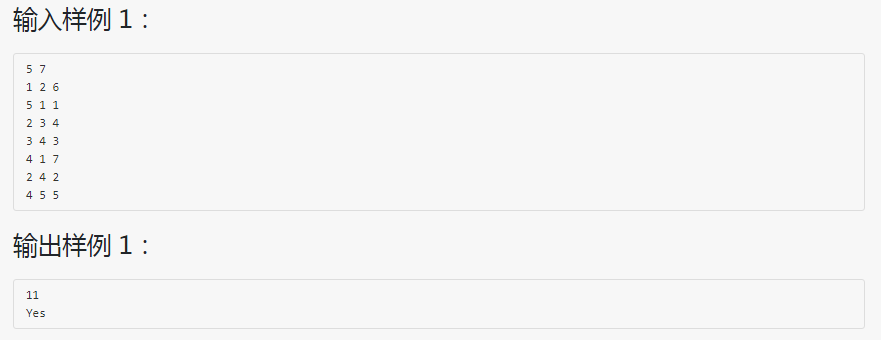
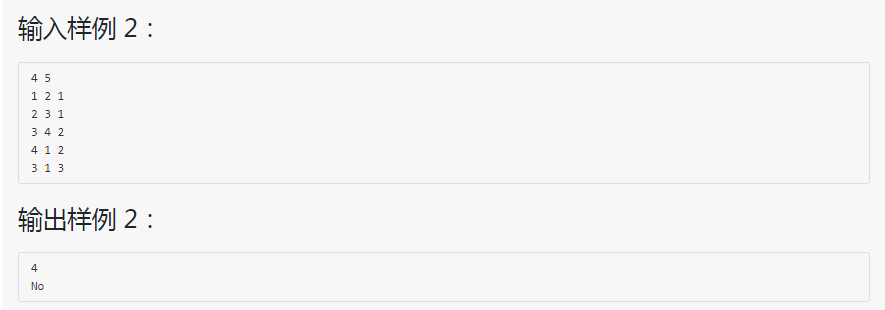
进阶实验6-3.6 最小生成树的唯一性 (35分)-并查集+Prim+次小生成树

 

 

 

 

 

 

 

 解题思路：

1、用并查集判断图的连通性

2、若是连通图，用prim算法计算最小生成树的权重

3、在连通图的基础上，求次小生成树判断最小生成树是否唯一

     标记最小生成树的使用的每条边，并记录其中有最大权重边；

     去掉最小生成树中权重最大边，再分别把未使用的各边加入再求最小权重

     如果此时求得的最小权重=之前求得的最小权重，则判断最小生成树不唯一，否则，唯一;

#include <stdio.h>
#include <string.h>
#define INF 0x3f3f3f3f
#define MaxVex 500+1
int G[MaxVex][MaxVex];
int used[MaxVex][MaxVex];//标记边是否使用
int Maxp[MaxVex][MaxVex];//记录最大边值
int visit[MaxVex];
int f[MaxVex];
int dist[MaxVex];
int pre[MaxVex];

int Nv,Ne;
int flag;
int getf(int x) {
    if(f[x]==x)
        return x;
    return f[x]=getf(f[x]);
}
void Merge(int x,int y) {
    int f1=getf(x);
    int f2=getf(y);
    f[f2]=f1;
}
void Init() {
    scanf("%d %d",&Nv,&Ne);
    int i,j;
    for(i=1; i<=Nv; i++) {
        f[i]=i;
    }
    memset(G,INF,sizeof(G));
    memset(visit,0,sizeof(visit));
    memset(used,0,sizeof(used));
    memset(Maxp,0,sizeof(Maxp));
    memset(pre,0,sizeof(pre));
    int v1,v2,x;
    for(i=0; i<Ne; i++) {
        scanf("%d %d %d",&v1,&v2,&x);
        G[v1][v2]=x;
        G[v2][v1]=G[v1][v2];
        Merge(v1,v2);
    }
    for(i=1; i<=Nv; i++) {
        dist[i]=G[1][i];
        pre[i]=1;
    }
}
int getcount() {
    int cnt=0;
    int i;
    for(i=1; i<=Nv; i++) {
        if(f[i]==i)
            cnt++;
    }
    return cnt;
}
int FindMin() {
    int min=0;
    int i;
    int MIN=INF;
    for(i=1; i<=Nv; i++) {
        if(!visit[i]&&dist[i]<MIN) {
            MIN=dist[i];
            min=i;
        }
    }
    return min;
}
//prim算法求最小生成树权重
int getMinDist() {
    int i;
    visit[1]=1;
    int sum=0;
    while(1) {
        int min=FindMin();
        if(min) {
            used[pre[min]][min]=used[min][pre[min]]=1;
            sum+=dist[min];
            visit[min]=1;
            for(i=1; i<=Nv; i++) {
                if(visit[i]&&i!=min)
                {
                    if(dist[min]>Maxp[i][pre[min]])
                    Maxp[min][i]=Maxp[i][min]=dist[min];
                    else
                    Maxp[min][i]=Maxp[i][min]=Maxp[i][pre[min]];
                }
                if(!visit[i]) {
                    if(G[min][i]<dist[i]) {
                        dist[i]=G[min][i];
                        pre[i]=min;
                    }
                }
            }
        } else
            break;
    }

    return sum;
}
int main() {
    Init();
    int count=getcount();
    if(count==1) {
        int sum=getMinDist();
        printf("%d\n",sum);
        //求次小生成树的权重
        int i,j;
        int ans=INF;
        for(i=1;i<=Nv;i++)
        {
            for(j=1;j<=Nv;j++)
            {
                if(i!=j&&!used[i][j])
                {
                    if(sum+G[i][j]-Maxp[i][j]<ans)
                    ans=sum+G[i][j]-Maxp[i][j];
                }
            }
        }
        if(ans==sum)
        printf("No");
        else
        printf("Yes");
    } else {
        printf("No MST\n%d",count);
    }
    return 0;
}