练习4.2 平衡二叉树的根 (25分)

 

 

输入样例1:

5
88 70 61 96 120

 

输出样例1:

70

 

输入样例2:

7
88 70 61 96 120 90 65

 

输出样例2:

88

解题思路：生成二叉排序树的同时调整为平衡二叉树
需要调整的情况：
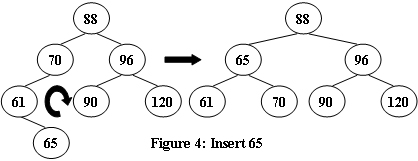
1、左单旋

 

2、右单旋

 

 

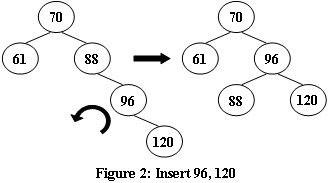
 3、先右旋后左旋

 

 

 4、先左旋后右旋

 

 

 

#include <stdio.h>
#include <malloc.h>
#define ElemType int
typedef struct BiTNode {
    ElemType Data;
    struct BiTNode *Left;
    struct BiTNode *Right;
}*AVLTree;
AVLTree SingleLeftRotation(AVLTree T) {//左单旋
    AVLTree B=T->Left;
    T->Left=B->Right;
    B->Right=T;
    return B;
}
AVLTree SingleRightRotation(AVLTree T) {//右单旋
    AVLTree B=T->Right;
    T->Right=B->Left;
    B->Left=T;
    return B;
}
AVLTree DoubleLeftRightRotation(AVLTree T) {//左右双旋
    T->Left=SingleRightRotation(T->Left);
    return SingleLeftRotation(T);
}
AVLTree DoubleRightLeftRotation(AVLTree T) {//右左双旋
    T->Right=SingleLeftRotation(T->Right);
    return SingleRightRotation(T);
}

AVLTree Insert(AVLTree T,ElemType X) {
    if(!T) {
        T=(AVLTree)malloc(sizeof(AVLTree));//每次新插入结点需申请空间
        T->Data=X;
        T->Left=NULL;
        T->Right=NULL;
    } else {
        if(X>T->Data) {//往右子树找位置
            T->Right=Insert(T->Right,X);
            if(GetHeight(T->Right)-GetHeight(T->Left)==2) {
                if(X<T->Right->Data) {
                    T=DoubleRightLeftRotation(T);
                } else T=SingleRightRotation(T);
            }
        } else if(X<T->Data) {//往左子树找位置
            T->Left=Insert(T->Left,X);
            if(GetHeight(T->Left)-GetHeight(T->Right)==2) {
                if(X>T->Left->Data) {
                    T=DoubleLeftRightRotation(T);
                } else T=SingleLeftRotation(T);
            }
        }
    }
    return T;

}
int GetHeight(AVLTree T) {//求树高
    if(!T)
        return 0;
    int hl=GetHeight(T->Left);
    int hr=GetHeight(T->Right);
    return (hl>hr?hl:hr)+1;
}
int main() {
    int n,x,i;
    scanf("%d",&n);
    AVLTree T=NULL;//初始化为NULL;
    for(i=0; i<n; i++) {
        scanf("%d",&x);
        T=Insert(T,x);
    }
    printf("%d",T->Data);
    return 0;
}