nand2tetris_ALU
这一节,我们将尝试构建CPU中的ALU单元。明明上一节才开始学习基本逻辑门,这一节就实现ALU,当时的我是吃惊的,但 确实仅用逻辑门就可以完成。在开始逐步实现之前,先补充一些前置知识
前置知识
HDL
上一节构建选择器时,得到了一个较长的函数式,那么如何验证函数表达式呢。课程老师提供了用于描述电路的HDL规范和解释运行的硬件模拟器,这些都在课程软件包中(之前实现MIT 6.824时,也是有各种模板代码和测试脚本,再次忍不住对Top大学的心向往之),执行示例图如下
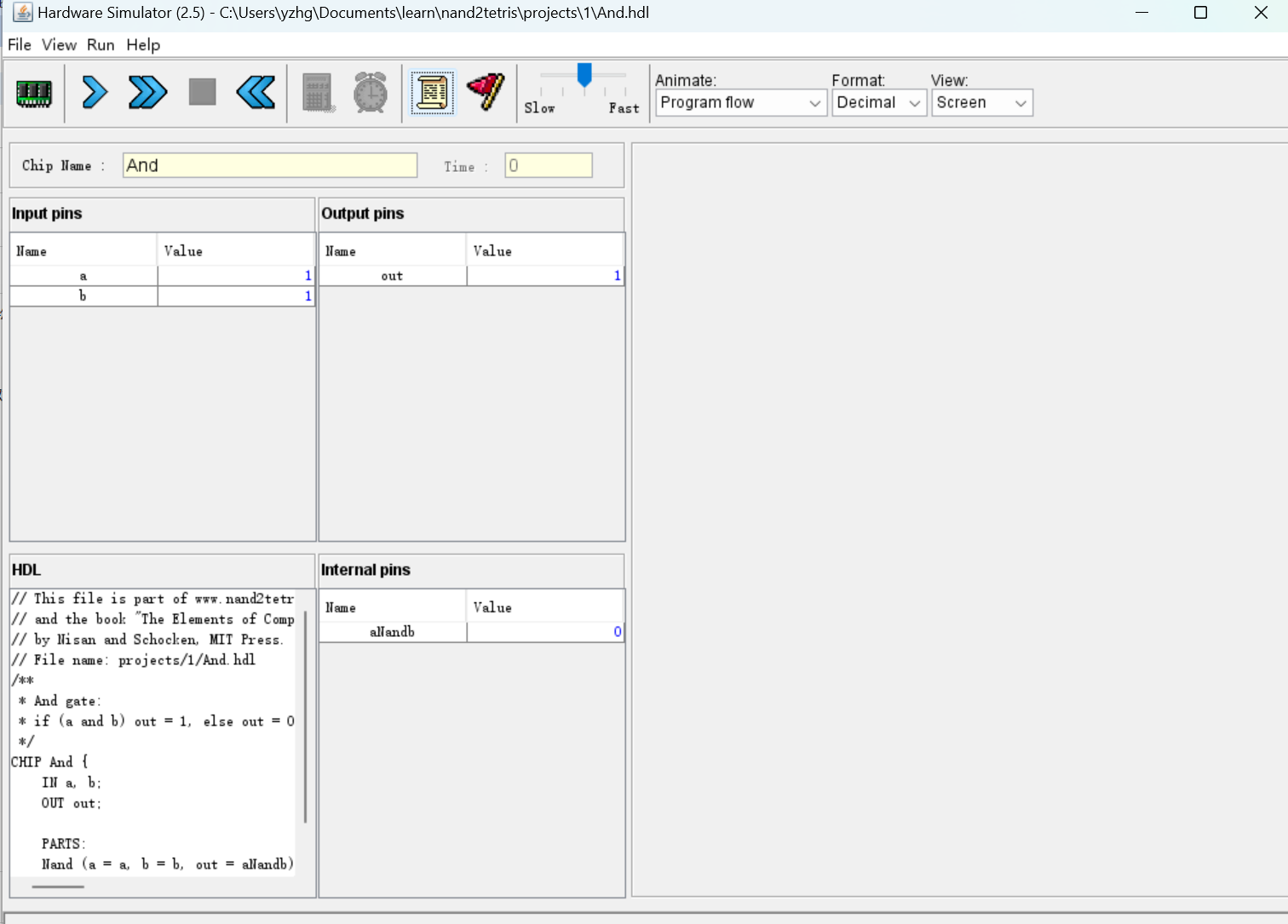
HDL引入
先来看一下之前的选择器的HDL实现,简单介绍一下HDL规范
// This file is part of www.nand2tetris.org
// and the book "The Elements of Computing Systems"
// by Nisan and Schocken, MIT Press.
// File name: projects/1/Mux.hdl
/**
* Multiplexor:
* if (sel = 0) out = a, else out = b
*/
CHIP Mux {
IN a, b, sel;
OUT out;
PARTS:
Not (in = sel, out = Notsel);
And (a = a, b = Notsel, out = aAndNotsel);
And (a = b, b = sel, out = bAndsel);
Or (a = aAndNotsel, b = bAndsel, out = out);
}
IN 定义输入形参名,OUT 定义输出形参名;Not可以理解为函数,in、a、b和out为函数参数名,sel和Notsel为函数传参;还有许多需要注意和特殊的语法的地方,一方面查看模拟器报错信息,另一方面参考老师标准实现,不建议在这里花费太多时间,毕竟我们只是学习思路
下面再介绍几个有趣的HDL实现,更好的感受HDL规范,对了,还有一点,HDL是电路图描述语言,如果出现电路回环,完全可以先使用变量,再声明(这一点,可能要在第三节寄存器实现)
有趣的HDL实现
多函数调用
/**
* Exclusive-or gate:
* if ((a and Not(b)) or (Not(a) and b)) out = 1, else out = 0
*/
CHIP Xor {
IN a, b;
OUT out;
PARTS:
Not (in = a, out = Nota);
Not (in = b, out = Notb);
And (a = a, b = Notb, out = aAndNotb);
And (a = b, b = Nota, out = bAndNota);
Or (a = aAndNotb, b = bAndNota, out = out);
}
多路总线的使用
/**
* 16-bit multiplexor:
* for i = 0, ..., 15:
* if (sel = 0) out[i] = a[i], else out[i] = b[i]
*/
CHIP Mux16 {
IN a[16], b[16], sel;
OUT out[16];
PARTS:
Mux (a = a[0], b = b[0], sel = sel, out = out[0]);
Mux (a = a[1], b = b[1], sel = sel, out = out[1]);
Mux (a = a[2], b = b[2], sel = sel, out = out[2]);
Mux (a = a[3], b = b[3], sel = sel, out = out[3]);
Mux (a = a[4], b = b[4], sel = sel, out = out[4]);
Mux (a = a[5], b = b[5], sel = sel, out = out[5]);
Mux (a = a[6], b = b[6], sel = sel, out = out[6]);
Mux (a = a[7], b = b[7], sel = sel, out = out[7]);
Mux (a = a[8], b = b[8], sel = sel, out = out[8]);
Mux (a = a[9], b = b[9], sel = sel, out = out[9]);
Mux (a = a[10], b = b[10], sel = sel, out = out[10]);
Mux (a = a[11], b = b[11], sel = sel, out = out[11]);
Mux (a = a[12], b = b[12], sel = sel, out = out[12]);
Mux (a = a[13], b = b[13], sel = sel, out = out[13]);
Mux (a = a[14], b = b[14], sel = sel, out = out[14]);
Mux (a = a[15], b = b[15], sel = sel, out = out[15]);
}
组合已有实现,实现更高级功能
/**
* 4-way 16-bit multiplexor:
* out = a if sel = 00
* b if sel = 01
* c if sel = 10
* d if sel = 11
*/
CHIP Mux4Way16 {
IN a[16], b[16], c[16], d[16], sel[2];
OUT out[16];
PARTS:
Mux16 (a = a, b = b, sel = sel[0], out = mux1);
Mux16 (a = c, b = d, sel = sel[0], out = mux2);
Mux16 (a = mux1, b = mux2, sel = sel[1], out = out);
}
二进制数
十进制数0-9,二进制数0-1,大于最大数时则进位。基本的二进制数容易理解,这里单独列出来,主要想讲一下负数,然后引出减法实现,毕竟一个ALU你不能算减法这太糟糕了,至于乘法和除法,则使用软件来实现吧
负数
一个四位的数,0000 - 1111,如果全部用来表示正数的话 0 - 15,这也被称为无符号表示。若想表示负数,取第一位做标识符,0为正,1为负,那么0000 - 0111,0 - 7;1111 - 1000,应该是-0? - -7?这里是直接根据二进制取反(0和1互换)来表示,只是-0 和 +0 是不是有一点点奇怪,一个0有两种表示的同时,还浪费了一个表示数。我们看下一种表示方法
要避免两个0的出现,负数则需要添加一个表示数,0、1.. 7、-8、-7..-1,二进制表示,0111 - 7,1000 - -8,1001 - -7,1111 - -1,我们再单独来看1和-1,0001 - 1,1111 - -1,二进制表示上 1 = -(-1) + 1。所以,你知道原码、反码和补码在描述什么了么
减法
加法规则 1 + 1 = 2,01 + 01 = 10。后面介绍加法器实现的时候,就会发现,加法是很容易通过基础逻辑门实现的,稍微提前一点,当前位是两个数的或运算结果,而进位则是两个数的与运算结果。那减法怎么办,01 - 01 = 00, 10 - 01 = 01,加法需要考虑的只是这一位是否需要向下一位进位,减法则要考虑借位了,那要借多少位呢,是不是有点复杂。当思考陷入僵局时,换一种思维吧
1 - 1 = 1 + (-1) = 0,10 - 01 = 0010 + (-0001)= 0010 + (-1 1111)= 0001.这里看着就有点绕了,为什么一会二进制,一会十进制的,这里是想借十进制的运算规则 减去一个数等于加上一个数的相反数,注意这里的相反数是十进制的取反,而不是二进制的取反。十进制的取反和二进制的取反是不一样的,因为我们没有-0的概念,-8多占了一位,所以十进制的取反 = 二进制的取反之后再加1
以前上学时候背诵的啊,负数的原码是1xxx,xxx是其正数时二进制表示形式,1表示负数;负数的反码等于原码的标识位不变,其余位取反;负数补码等于负数的反码+1,负数的补码常用来进行减法运算,那么你现在明白为什么了吧
打开自带计算器-程序员模式,验证一下
计算 5 - 3,假设第四位为标志位
5 + (-3)= 0101 + (!1011 + 1) = 0101 + (1100 + 1) = 0101 + 1101 = 0010 = 2
逐步实现ALU
半加器
这个为什么叫半加器呢,因为两个半加器可以合成全加器
/**
* Computes the sum of two bits.
*/
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b
carry; // Left bit of a + b
PARTS:
And(a=a,b=b,out=carry);
Xor(a=a,b=b,out=sum);
}
全加器
半加器的功能对于实现加法是不够的,因为加法是需要三个入参的,即 两个输入数和一个来自低位的进位(初始进位为0)。那么把两个半加器合起来就好了啊
/**
* Computes the sum of three bits.
*/
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder(a=a,b=b,sum=sum1,carry=carry1);
HalfAdder(a=sum1,b=c,sum=sum,carry=carry2);
Or(a=carry1,b=carry2,out=carry);
}
16位加法
这里会不会恍惚一下,我们可以实现16位加法了!实现思路也很简单,一位一位的加起来就好了
/**
* 16-bit adder: Adds two 16-bit two's complement values.
* The most significant carry bit is ignored.
*/
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
HalfAdder (a = a[0], b = b[0], sum = out[0], carry = carry0);
FullAdder (a = carry0, b = a[1], c = b[1], sum = out[1], carry = carry1);
FullAdder (a = carry1, b = a[2], c = b[2], sum = out[2], carry = carry2);
FullAdder (a = carry2, b = a[3], c = b[3], sum = out[3], carry = carry3);
FullAdder (a = carry3, b = a[4], c = b[4], sum = out[4], carry = carry4);
FullAdder (a = carry4, b = a[5], c = b[5], sum = out[5], carry = carry5);
FullAdder (a = carry5, b = a[6], c = b[6], sum = out[6], carry = carry6);
FullAdder (a = carry6, b = a[7], c = b[7], sum = out[7], carry = carry7);
FullAdder (a = carry7, b = a[8], c = b[8], sum = out[8], carry = carry8);
FullAdder (a = carry8, b = a[9], c = b[9], sum = out[9], carry = carry9);
FullAdder (a = carry9, b = a[10], c = b[10], sum = out[10], carry = carry10);
FullAdder (a = carry10, b = a[11], c = b[11], sum = out[11], carry = carry11);
FullAdder (a = carry11, b = a[12], c = b[12], sum = out[12], carry = carry12);
FullAdder (a = carry12, b = a[13], c = b[13], sum = out[13], carry = carry13);
FullAdder (a = carry13, b = a[14], c = b[14], sum = out[14], carry = carry14);
FullAdder (a = carry14, b = a[15], c = b[15], sum = out[15], carry = carry15);
}
自增器
实现++1,单独列出来,我想这个很有用。执行程序时,程序指针大部分情况就是+1 +1的
/**
* 16-bit incrementer:
* out = in + 1
*/
CHIP Inc16 {
IN in[16];
OUT out[16];
PARTS:
Add16(a=in,b[0]=true,b[1..15]=false,out=out);
}
ALU
我们终于来到了这一步,不过先调整一下期望值,这里的ALU只实现加法减法、与或非和置零基础运算。这是怎么实现的呢,人为设置了多个开关位,不同的设置来达到目的
/**
* ALU (Arithmetic Logic Unit):
* Computes out = one of the following functions:
* 0, 1, -1,
* x, y, !x, !y, -x, -y,
* x + 1, y + 1, x - 1, y - 1,
* x + y, x - y, y - x,
* x & y, x | y
* on the 16-bit inputs x, y,
* according to the input bits zx, nx, zy, ny, f, no.
* In addition, computes the two output bits:
* if (out == 0) zr = 1, else zr = 0
* if (out < 0) ng = 1, else ng = 0
*/
// Implementation: Manipulates the x and y inputs
// and operates on the resulting values, as follows:
// if (zx == 1) sets x = 0 // 16-bit constant
// if (nx == 1) sets x = !x // bitwise not
// if (zy == 1) sets y = 0 // 16-bit constant
// if (ny == 1) sets y = !y // bitwise not
// if (f == 1) sets out = x + y // integer 2's complement addition
// if (f == 0) sets out = x & y // bitwise and
// if (no == 1) sets out = !out // bitwise not
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute (out = x + y) or (out = x & y)?
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // if (out == 0) equals 1, else 0
ng; // if (out < 0) equals 1, else 0
PARTS:
Mux16(a=x,b=false,sel=zx,out=x1);
Not16(in=x1,out=notx1);
Mux16(a=x1,b=notx1,sel=nx,out=x2);
Mux16(a=y,b=false,sel=zy,out=y1);
Not16(in=y1,out=noty1);
Mux16(a=y1,b=noty1,sel=ny,out=y2);
Add16(a=x2,b=y2,out=out1);
And16(a=x2,b=y2,out=out2);
Mux16(a=out2,b=out1,sel=f,out=out3);
Not16(in=out3,out=notout3);
Mux16(a=out3,b=notout3,sel=no,out=out,out[0..7]=out4,out[8..15]=out5,out[15]=ng);
Or8Way(in=out4,out=or1);
Or8Way(in=out5,out=or2);
Or(a=or1,b=or2,out=or3);
Mux(a=true,b=false,sel=or3,out=zr);
}
这里实现上逐一利用选择器设置合适的值,难点应该是最后两个标志位的设值,如果不知道HDL可以这样表述(最后Mux16这里),还是要多写很多代码的,而且过程中会收到无数次编辑器的提示
可是这怎么用呢。具体的执行逻辑见下表,选一个x-y介绍。更多的,也可以依样推导出来,这里最难的是怎么想到设置这几个开关位就能达到这个效果的,恰好 这个问题是我们不用深究的
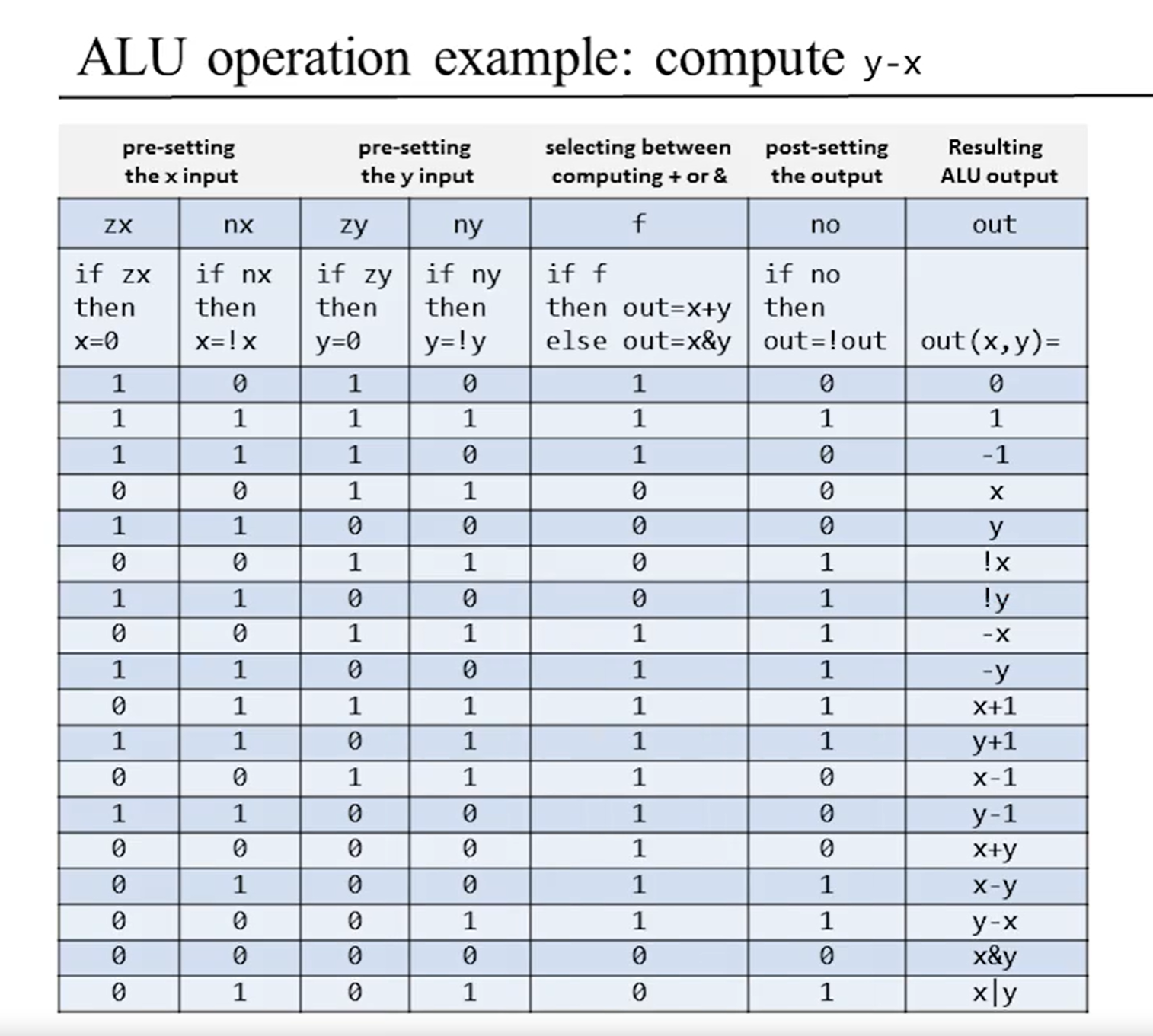
x-y
置1的位置为,x=!x x+y -out,out = -(-x + y) = x - y
总结
这节课程的跳跃有点大,好在用到的都是一些熟悉概念,复杂的点在于文字需求 -> 程序代码 -> HDL规范过程中的思维转换,最后的ALU反而并没有想象中那么复杂


 浙公网安备 33010602011771号
浙公网安备 33010602011771号