并查集

leetcode1月的每日打卡题，大部分是可以使用并查集求解的，“并查集月”。简单回顾一下并查集的基础结构

并查集解决了什么问题

并查集主要解决连接问题。这里的连接可以是具体的网络节点，也可以是抽象的社交网络，并查集只关心两点之间是否可以通过一条路径连接起来，而不考虑两点怎么连接起来的。可以发现，并查集比BFS回答的问题要少，所以若只需要回答两点是否连接，优先考虑并查集

并查集接口定义

public interface UF{
    boolean isConnected(int p, int q);
    void union(int p, int q);
}

简单实现

每个集合都有自己的编号，同一个集合的元素编号相同。数组实现，每个下标标识一个元素，数组中存放每个元素所属的集合编号

元素	0	1	2	3	4	5
集合编号	1	0	1	0	1	0
这里，0、2、4属于集合1，而1、3、5属于集合0

public class UnionFind implements UF{
    private int[] id;
    public UnionFind(int size) {
        id = new int[size];
        // 开始时，每个元素都属于不同的集合
        for(int i=0;i<id.length;i++) {
            id[i] = i;
        }
    }
    
    // 查找元素p所对应的集合编号 O(1)
    private int find(int p) {
        return id[p];
    }
    
    // 查找元素p，q是否属于同一个集合
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
    
    // 合并元素p和元素q所属的集合 O(n)
    public void union(int p, int q) {
        int pId = find(p);
        int qId = find(q);
        
        if(pId == qId) {
            return;
        }
        for(int i=0;i<id.length;i++) {
            if(id[i]==pId) {
                id[i] = qId;
            }
        }
    }

}

这里方式实现的并查集查找效率较高，但是合并效率较低，下面介绍并查集真正的结构

我们约定一棵子节点指向父节点的树结构，根节点的父节点是它本身，可能有多个根节点，它们各自组成一个集合。这样，我们通过查询两个节点的根节点是否相同，来判断二者是否属于同一个集合；合并的时候只需要将一棵树的根节点指向另一棵树的根节点

基础实现

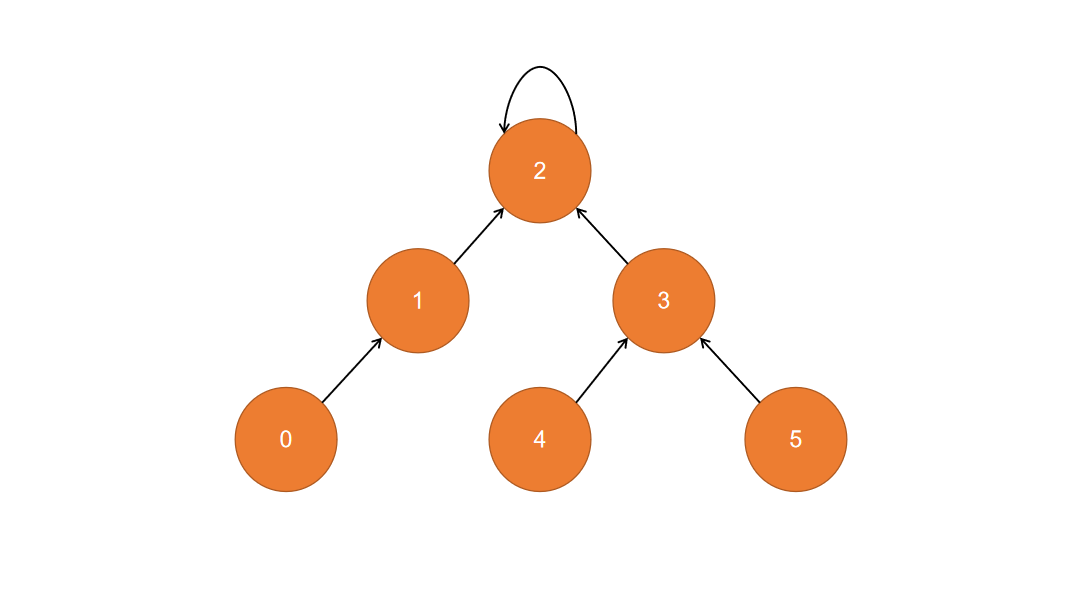
这里，同样可以使用数组实现，下面表格中构成一棵以2为根节点的树

元素	0	1	2	3	4	5
集合编号	1	2	2	2	3	3

public class UnionFind implements UF{
    private int[] parent;
    public UnionFind(int size) {
        parent = new int[size];
        // 开始时，每个元素都属于不同的集合
        for(int i=0;i<parent.length;i++) {
            parent[i] = i;
        }
    }
    
    // 查找元素p所对应的集合编号
    // O(h)复杂度，h为树的高度
    private int find(int p) {
        while(p != parent[p]) {
            p = parent[p];
        }
        return p;
    }
    
    // 查找元素p，q是否属于同一个集合
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
    
    // 合并元素p和元素q所属的集合 O(h)
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        
        if(pRoot == qRoot) {
            return;
        }
        
        parent[pRoot] = qRoot;
    }
}

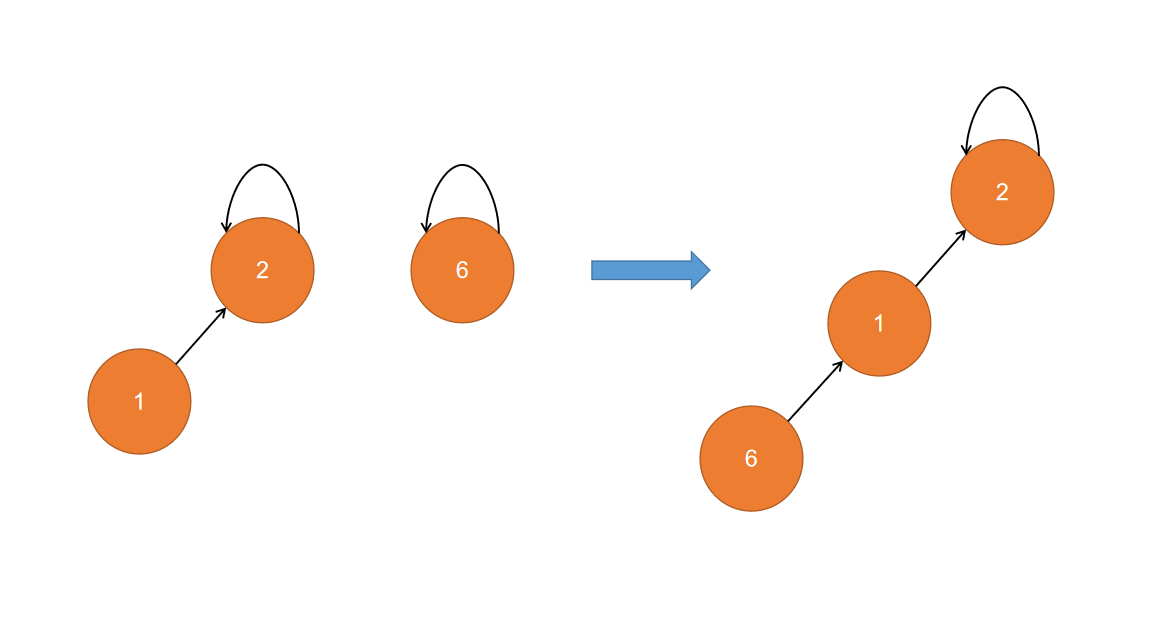
这种实现方式合并时直接将一个节点指向另一个节点，很容易变成下图这样，为了避免出现近似于链表的结构，有两种优化方式，按秩合并和路径压缩，二者优化的点不一样，不过均是为了让树尽可能的层次少一点

按秩合并

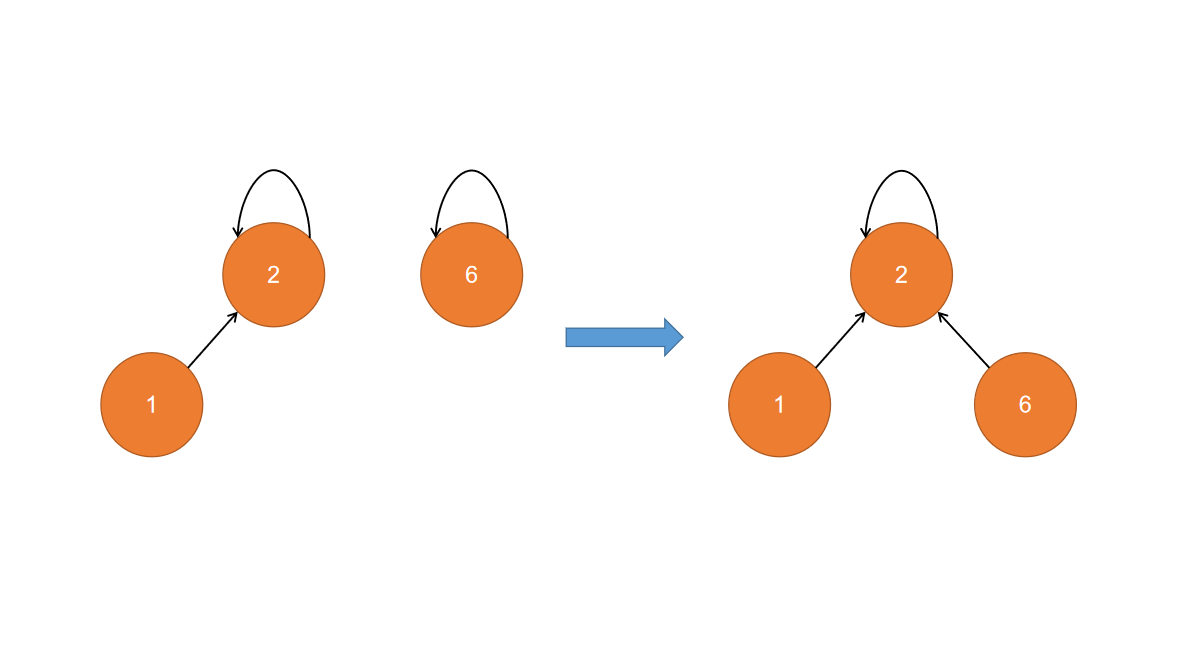
这种方式，是在集合合并时，通过一定的策略，来决定节点指向。通常选取以该节点为根节点的子节点个数或者树的(相对)高度

基于size的优化

这里应该是让6指向2，而不是2指向6，2的子节点数更多(当然，2的树结构也较高，不过也许你恰好需要统计子节点个数)

public class UnionFind implements UF{
    private int[] parent;
    // sz[i]表示以i为根的集合中元素个数
    private int[] sz;
    public UnionFind(int size) {
        parent = new int[size];
        sz = new int[size];
        
        // 开始时，每个元素都属于不同的集合
        for(int i=0;i<parent.length;i++) {
            parent[i] = i;
            sz[i] = 1;
        }
    }
    
    // 查找元素p所对应的集合编号
    // O(h)复杂度，h为树的高度
    private int find(int p) {
        while(p != parent[p]) {
            p = parent[p];
        }
        return p;
    }
    
    // 查找元素p，q是否属于同一个集合
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
    
    // 合并元素p和元素q所属的集合 O(h)
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        
        if(pRoot == qRoot) {
            return;
        }
        
        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if(sz[pRoot] < sz[qRoot]) {
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else{
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }       
    }

}

基于rank的优化

还有一种更为直观的是合并策略是，根据根节点子节点树的高度来判断

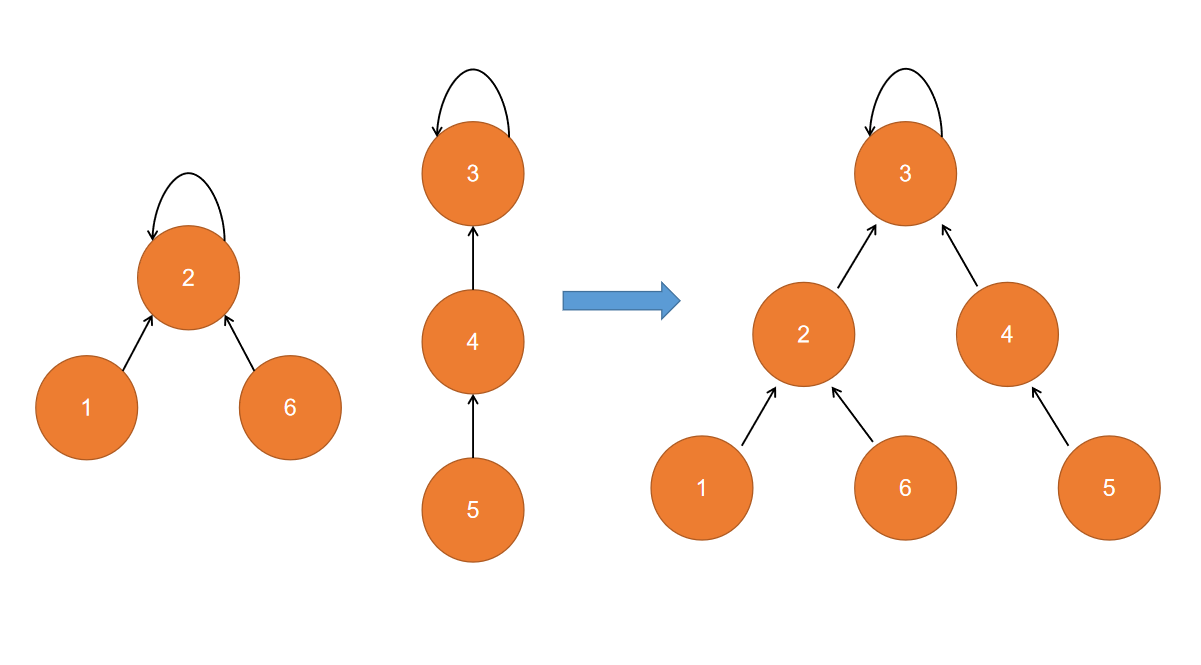
有时，子节点数的多少不一定可以代表树的层数。至于不用height来表达，主要考虑后面的路径压缩会改变树的结构，转而使用rank来表示一种相对顺序

public class UnionFind implements UF{
    private int[] parent;
    // rank[i]表示以i为根的集合中树的层数
    private int[] rank;
    public UnionFind(int size) {
        parent = new int[size];
        rank = new int[size];
        
        // 开始时，每个元素都属于不同的集合
        for(int i=0;i<parent.length;i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }
    
    // 查找元素p所对应的集合编号
    // O(h)复杂度，h为树的高度
    private int find(int p) {
        while(p != parent[p]) {
            p = parent[p];
        }
        return p;
    }
    
    // 查找元素p，q是否属于同一个集合
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
    
    // 合并元素p和元素q所属的集合 O(h)
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        
        if(pRoot == qRoot) {
            return;
        }
        
        // 根据两个元素所在树的rank不同判断合并方向
        // 将rank低的集合合并到rank高的集合上
        if(rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if(rank[pRoot] > rank[qRoot]){
            parent[qRoot] = pRoot;
        } else{
            parent[pRoot] = qRoot;
            rank[qRoot]++;
        }       
    }

}

路径压缩

这种优化思路就是在查询(find)时改变树的结构，降低树的高度。也有两种思路，区别只是递归与非递归，一步到位或者多次调整

子节点直接指向根节点

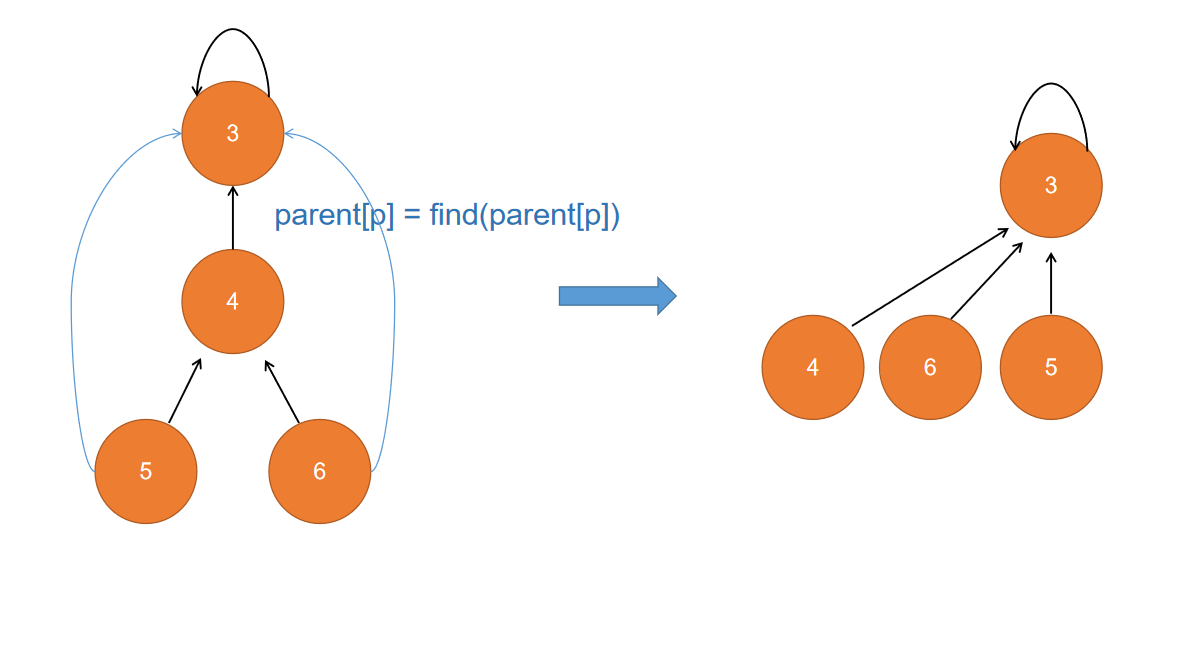
private int find(int p) {
    if(p == parent[p]) {
        return p;
    }
    return parent[p] = find(parent[p]);
}

节点指向其父节点的父节点

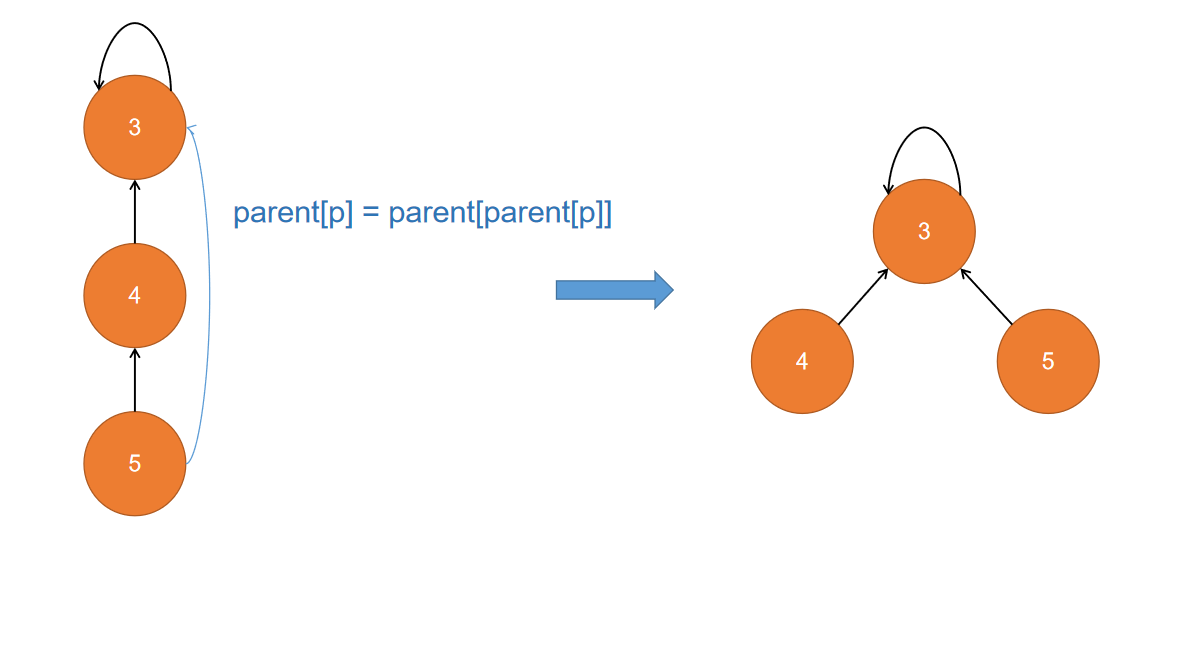
private int find(int p) {
    while(p != parent[p]) {
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

「路径压缩」和「按秩合并」一起使用的时候，难以维护「秩」准确的定义，但依然具有参考价值。这是因为：虽然 rank 不是此时树的精确高度，但是不会出现树 a 的高度比树 b 结点高，但是树 a 的 rank 却比树 b 的 rank 低的情况
在实际解决问题的时候，一般只用「路径压缩」。如果「路径压缩」的结果不太理想，再考虑使用「按秩合并」。虽然「路径压缩」和「按秩合并」同时使用在理论上会使得时间复杂度降低，但在数据规模有限的情况下，这种优化可能不能加快程序的执行时间