关于阶乘,老郭和宝宝等前辈做了大量研究,计算速度也达到了非常快的水准。本文宗旨不在于和他们比快,因为他们专门为阶乘做了很多优化。本文介绍的是使用C#直接计算的方法,速度虽然不能跟他们相比,但在一般场合下使用应该是足够的。本文的思想其实是ACM中的一个基本函数,做了一定改动。
这个类中用到了10000进制表示法,我做了一定的尝试,发现在100000进制的情况下速度最快,以下是耗费时间统计表(单位:ms),其中行表示要计算的阶乘,列表示进制。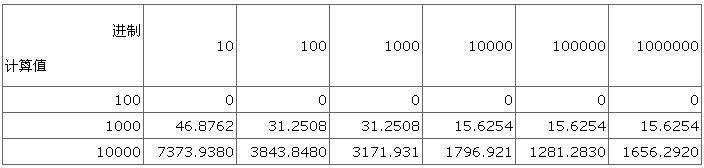
用这个类计算100000!花费263819.2536ms,结果见:http://blog.csdn.net/Snowdust/archive/2010/03/18/5393350.aspx
代码如下:
//-----------------------------------------------------------------------------
//
// 算法:阶乘类
//
// 版权所有(C) Snowdust
// 个人博客 http://blog.csdn.net/snwodust & http://snowdust.cnblogs.com
// MSN & Email snwodust77@sina.com
//
// 此源代码可免费用于各类软件(含商业软件)
// 允许对此代码的进一步修改与开发
// 但必须完整保留此版权信息
//
// 调用方法如下:
// int num = 10000;
// Arithmetic.Factorial f = new Arithmetic.Factorial(num);
// List<int> result = f.Calculate();
// String ret = f.ToString();
// 返回结果:result为100000进制表示的范型,ret为转换成十制制的字符串
//
// 版本历史:
// V0.1 2010-03-17 摘要:首次创建
//
//-----------------------------------------------------------------------------
using System;
using System.Collections.Generic;
using System.Text;
namespace Arithmetic
{
public class Factorial
{
#region 定义属性
/// <summary>
/// 进制
/// </summary>
private int m_BaseNumber = 100000;
public int BaseNumber
{
get
{
return m_BaseNumber;
}
}
/// <summary>
/// 待求阶乘的数
/// </summary>
private int m_Number;
/// <summary>
/// 结果
/// </summary>
private List<int> m_Result = new List<int>();
#endregion
#region 构造函数
/// <summary>
/// 构造函数
/// </summary>
/// <param name="n">待求阶乘的数</param>
public Factorial(int n)
{
m_Number = n;
m_Result = new List<int>();
}
#endregion
#region 方法
/// <summary>
/// 计算阶乘
/// </summary>
/// <returns>结果范型</returns>
public List<int> Calculate()
{
int digit = (int)System.Math.Log10(m_BaseNumber);
int len = (int)(m_Number * System.Math.Log10((m_Number + 1) / 2)) / digit;//计算n!有数数字的个数
len += 2; //保险起见,加长2位
int[] a = new int[len];
int i, j;
long c;
int m = 0;
a[0] = 1;
for (i = 2; i <= m_Number; i++)
{
c = 0;
for (j = 0; j <= m; j++)
{
long t = a[j] * i + c;
c = t / m_BaseNumber;
a[j] = (int)(t % m_BaseNumber);
}
while (c > 0)
{
m++;
a[m] = (int)(c % m_BaseNumber);
c = c / m_BaseNumber;
}
}
for (i = 0; i <= m; i++)
{
m_Result.Add(a[i]);
}
return m_Result;
}
/// <summary>
/// 重写ToString方法
/// </summary>
/// <returns>结果字符串</returns>
public override string ToString()
{
if (m_Result.Count == 0)
{
Calculate();
}
StringBuilder sb = new StringBuilder();
int digit = (int)System.Math.Log10(m_BaseNumber);
sb.Append(m_Result[m_Result.Count - 1]);
for (int i = m_Result.Count - 2; i >= 0; i--)
{
sb.Append(m_Result[i].ToString().PadLeft(digit, '0'));
}
return sb.ToString();
}
#endregion
}
}
//
// 算法:阶乘类
//
// 版权所有(C) Snowdust
// 个人博客 http://blog.csdn.net/snwodust & http://snowdust.cnblogs.com
// MSN & Email snwodust77@sina.com
//
// 此源代码可免费用于各类软件(含商业软件)
// 允许对此代码的进一步修改与开发
// 但必须完整保留此版权信息
//
// 调用方法如下:
// int num = 10000;
// Arithmetic.Factorial f = new Arithmetic.Factorial(num);
// List<int> result = f.Calculate();
// String ret = f.ToString();
// 返回结果:result为100000进制表示的范型,ret为转换成十制制的字符串
//
// 版本历史:
// V0.1 2010-03-17 摘要:首次创建
//
//-----------------------------------------------------------------------------
using System;
using System.Collections.Generic;
using System.Text;
namespace Arithmetic
{
public class Factorial
{
#region 定义属性
/// <summary>
/// 进制
/// </summary>
private int m_BaseNumber = 100000;
public int BaseNumber
{
get
{
return m_BaseNumber;
}
}
/// <summary>
/// 待求阶乘的数
/// </summary>
private int m_Number;
/// <summary>
/// 结果
/// </summary>
private List<int> m_Result = new List<int>();
#endregion
#region 构造函数
/// <summary>
/// 构造函数
/// </summary>
/// <param name="n">待求阶乘的数</param>
public Factorial(int n)
{
m_Number = n;
m_Result = new List<int>();
}
#endregion
#region 方法
/// <summary>
/// 计算阶乘
/// </summary>
/// <returns>结果范型</returns>
public List<int> Calculate()
{
int digit = (int)System.Math.Log10(m_BaseNumber);
int len = (int)(m_Number * System.Math.Log10((m_Number + 1) / 2)) / digit;//计算n!有数数字的个数
len += 2; //保险起见,加长2位
int[] a = new int[len];
int i, j;
long c;
int m = 0;
a[0] = 1;
for (i = 2; i <= m_Number; i++)
{
c = 0;
for (j = 0; j <= m; j++)
{
long t = a[j] * i + c;
c = t / m_BaseNumber;
a[j] = (int)(t % m_BaseNumber);
}
while (c > 0)
{
m++;
a[m] = (int)(c % m_BaseNumber);
c = c / m_BaseNumber;
}
}
for (i = 0; i <= m; i++)
{
m_Result.Add(a[i]);
}
return m_Result;
}
/// <summary>
/// 重写ToString方法
/// </summary>
/// <returns>结果字符串</returns>
public override string ToString()
{
if (m_Result.Count == 0)
{
Calculate();
}
StringBuilder sb = new StringBuilder();
int digit = (int)System.Math.Log10(m_BaseNumber);
sb.Append(m_Result[m_Result.Count - 1]);
for (int i = m_Result.Count - 2; i >= 0; i--)
{
sb.Append(m_Result[i].ToString().PadLeft(digit, '0'));
}
return sb.ToString();
}
#endregion
}
}




