99 Lisp Problems 二叉树(P54~P69)
P54A (*) Check whether a given term represents a binary tree
Write a predicate istree which returns true if and only if its argument is a list representing a binary tree.
Example:
(istree (a (b nil nil) nil))
T
(istree (a (b nil nil)))
NIL
(define (istree tree)
(if (or (eq? 'nil tree) (null? tree)) #t ;empty is a tree
(if (not (= (length tree) 3)) #f;
(let ([root (not (pair? (car tree)))]
[left (istree (cadr tree))]
[right (istree (caddr tree))])
(and root left right)))))
P55 (**) Construct completely balanced binary trees
In a completely balanced binary tree, the following property holds for every node:
The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal,
which means their difference is not greater than one.
Write a function cbal-tree to construct completely balanced binary trees for a given number of nodes.
The predicate should generate all solutions via backtracking. Put the letter 'x' as information into all
nodes of the tree.
Example:
cbal-tree(4,T).
T = t(x, t(x, nil, nil), t(x, nil, t(x, nil, nil))) ;
T = t(x, t(x, nil, nil), t(x, t(x, nil, nil), nil)) ;
etc......No
构造完全平衡二叉树,完全平衡二叉树的定义是左右子树的节点数量相差不超过1。
算法执行步骤:
构造节点数量为(n - 1)/2的完全平衡树集合s1
构造节点数量为n - (n - 1)/2的完全平衡树集合s2
从s1中取元素作为左子树,从s2中取元素作为右子树.
如果s1 != s2
从s2中取元素作为左子树,从s1中取元素作为右子树.
(define (cbal-tree n)
(define (iter n result)
(if (<= n 0) '(nil)
(let* ([n1 (floor (/ (- n 1) 2))]
[n2 (- (- n 1) n1)]
[sub1 (iter n1 result)]
[sub2 (iter n2 result)]
[r (if (not (equal? sub1 sub2))
(foldr (lambda (x1 acc1)
(append (foldr (lambda (x2 acc2)
(cons (list 'x x1 x2) acc2)) '() sub2) acc1))
'() sub1) '() )])
(append r (append (foldr (lambda (x1 acc1)
(append (foldr (lambda (x2 acc2)
(cons (list 'x x2 x1) acc2)) '() sub2) acc1))
'() sub1) result)))))
(iter n '()))
P56 (**) Symmetric binary trees
Let us call a binary tree symmetric if you can draw a vertical line through the root
node and then the right subtree is the mirror image of the left subtree. Write a predicate
symmetric/1 to check whether a given binary tree is symmetric. Hint: Write a predicate mirror/2
first to check whether one tree is the mirror image of another. We are only interested in the
structure, not in the contents of the nodes.
(define (sametree? tree1 tree2)
(cond [(or (and (pair? tree1) (not (pair? tree2)))
(and (pair? tree2) (not (pair? tree1)))) #f]
[(and (eq? 'nil tree1) (eq? 'nil tree2)) #t]
[else (and (sametree? (cadr tree1) (cadr tree2)) (sametree? (caddr tree1) (caddr tree2)))]))
(define (mirror? tree1 tree2);tree1的左子树结构==tree2的右子树且tree1的右子树结构==tree2的左子树则两树是镜像
(and (sametree? (cadr tree1) (caddr tree2)) (sametree? (caddr tree1) (cadr tree2))))
(define (symmetric tree) (mirror? (cadr tree) (caddr tree)))
P57 (**) Binary search trees (dictionaries)
Use the predicate add/3, developed in chapter 4 of the course,
to write a predicate to construct a binary search tree from a list of integer numbers.
Example:
construct([3,2,5,7,1],T).
T = t(3, t(2, t(1, nil, nil), nil), t(5, nil, t(7, nil, nil)))
Then use this predicate to test the solution of the problem P56.
Example:
test-symmetric([5,3,18,1,4,12,21]).
Yes
test-symmetric([3,2,5,7,1]).
No
(define (construct xs)
(define (add x tree)
(if (or (null? tree) (eq? 'nil tree)) (list x 'nil 'nil)
(if (> x (car tree)) (list (car tree) (cadr tree) (add x (caddr tree)))
(list (car tree) (add x (cadr tree)) (caddr tree)))))
(define (iter xs tree)
(if (null? xs) tree
(iter (cdr xs) (add (car xs) tree))))
(iter xs '()))
P58 (**) Generate-and-test paradigm
Apply the generate-and-test paradigm to construct all symmetric,
completely balanced binary trees with a given number of nodes. Example:
sym-cbal-trees(5,Ts).
Ts = [t(x, t(x, nil, t(x, nil, nil)), t(x, t(x, nil, nil), nil)), t(x, t(x, t(x, nil, nil), nil), t(x, nil, t(x, nil, nil)))]
How many such trees are there with 57 nodes? Investigate about how many solutions there are for a given number of nodes?
What if the number is even? Write an appropriate predicate.
(define (sym-cbal-trees n)
(let ([trees (cbal-tree n)])
(foldr (lambda (x acc) (if (symmetric x) (cons x acc) acc))
'() trees)))
P59 (**) Construct height-balanced binary trees
In a height-balanced binary tree, the following property holds for every node:
The height of its left subtree and the height of its right subtree are almost equal,
which means their difference is not greater than one.
Write a predicate hbal-tree/2 to construct height-balanced binary trees for a given height.
The predicate should generate all solutions via backtracking. Put the letter 'x' as information
into all nodes of the tree.
Example:
hbal-tree(3,T).
T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil), t(x, nil, nil))) ;
T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil), nil)) ;
etc......No
(define (hbal-tree h)
;高度为2的高度平衡树只有
; x x x
; x nil nil x x x
;三种
(cond [(= 1 h) (list '(x nil nil))]
[(= 2 h) (list '(x (x nil nil) nil) '(x nil (x nil nil)) '(x (x nil nil) (x nil nil)))]
[else (let* ([sub1 (hbal-tree (- h 1))] ;所有高度为h-1的子树
[sub2 (hbal-tree (- h 2))] ;所有高度为h-2的子树
[t1 (foldr (lambda (x1 acc1)
(append (foldr (lambda (x2 acc2)
(cons (list 'x x2 x1) acc2)) '() sub1) acc1)) '() sub2)]
[t2 (foldr (lambda (x1 acc1)
(append (foldr (lambda (x2 acc2)
(cons (list 'x x1 x2) acc2)) '() sub1) acc1)) '() sub2)]
[t3 (foldr (lambda (x1 acc1)
(append (foldr (lambda (x2 acc2)
(cons (list 'x x2 x1) acc2)) '() sub1) acc1)) '() sub1)])
(append t1 t2 t3))]))
P60 () Construct height-balanced binary trees with a given number of nodes
Consider a height-balanced binary tree of height H. What is the maximum number of nodes it can contain?
Clearly, MaxN = 2H - 1. However, what is the minimum number MinN? This question is more difficult.
Try to find a recursive statement and turn it into a predicate minNodes/2 defined as follwos:
% minNodes(H,N) :- N is the minimum number of nodes in a height-balanced binary tree of height H.
(integer,integer), (+,?)
On the other hand, we might ask: what is the maximum height H a height-balanced binary tree with N nodes can have?
% maxHeight(N,H) :- H is the maximum height of a height-balanced binary tree with N nodes
(integer,integer), (+,?)
Now, we can attack the main problem: construct all the height-balanced binary trees with a given nuber of nodes.
% hbal-tree-nodes(N,T) :- T is a height-balanced binary tree with N nodes.
Find out how many height-balanced trees exist for N = 15.
(define (exponent x n)
(cond [(= 0 n) 1]
[(= 1 n) x]
[else (* x (exponent x (- n 1)))]))
(define (maxNodes h) (- (exponent 2 h) 1))
;高度为h的具有最少内节点数量的高度平衡树其两棵子树必定一棵是高度为h-1
;具有最少内节点数量的高度平衡树,一棵是高度为h-2具有最少内节点数量的高度平衡树
;高度为0,最少内节点数量为0,高度为1,最小内节点数量为1,高度为2最少內节点数量为2
;minNodes(h) = 1 ,h == 1
;minNodes(h) = 2 ,h == 2
;minNodes(h) = minNodes( h - 1 ) + minNodes(h - 2) + 根节点,h == 3
; = minNodes(2) + minNodes(1) + 1 = 4
(define (minNodes h)
(cond [(= 0 h) 0]
[(= 1 h) 1]
[(= 2 h) 2]
[else (+ 1 (+ (minNodes (- h 1)) (minNodes (- h 2))))]))
;maxHeight N个节点的高度平衡树的最大高度
;解法1)从h=1开始调用minNodes,如果N >= minNodes(h) and minNodes(h+1) > N ,则h就是最大高度
(define (maxHeight n)
(define (iter h)
(if (and (>= n (minNodes h)) (> (minNodes (+ h 1)) n)) h
(iter (+ h 1))))
(if (= n 0) 0
(iter 1)))
(define (minHeight n) (ceiling (log (+ n 1) 2)))
(define (countNode tree)
(if (eq? 'nil tree) 0
(+ 1 (+ (countNode (cadr tree)) (countNode (caddr tree))))))
;hbal-tree-nodes
;解法1)通过maxHeight获得树的最大高度H,通过minHeight获得最小高度h
;通过hbal-tree构造h~H之间的所有高度平衡树,过滤掉节点数量不为n的
(define (hbal-tree-nodes n)
(let* ([maxh (maxHeight n)]
[minh (minHeight n)]
[rangeh (range minh maxh)]
[all (foldl (lambda (acc x)
(append (hbal-tree x) acc)) '() rangeh)])
(foldl (lambda (acc x)
(if (= (countNode x) n) (cons x acc) acc))
'() all)))
P61 (*) Count the leaves of a binary tree
A leaf is a node with no successors. Write a predicate count-leaves/2 to count them.
% count-leaves(T,N) :- the binary tree T has N leaves
(define (count-leaves tree)
(if (eq? tree 'nil) 0
(let ([rcount (count-leaves (cadr tree))]
[lcount (count-leaves (caddr tree))])
(if (and (= 0 rcount) (= 0 lcount)) 1
(+ rcount lcount)))))
P61A (*) Collect the leaves of a binary tree in a list
A leaf is a node with no successors. Write a predicate leaves/2 to collect them in a list.
% leaves(T,S) :- S is the list of all leaves of the binary tree T
(define (leaves tree)
(if (eq? tree 'nil) '()
(let ([left (cadr tree)]
[right (caddr tree)])
(if (and (eq? left 'nil) (eq? right 'nil))
(list tree)
(append (leaves left) (leaves right))))))
P62 (*) Collect the internal nodes of a binary tree in a list
An internal node of a binary tree has either one or two non-empty successors.
Write a predicate internals/2 to collect them in a list.
% internals(T,S) :- S is the list of internal nodes of the binary tree T.
(define (internals tree)
(if (eq? tree 'nil) '()
(let ([left (cadr tree)]
[right (caddr tree)])
(if (not (and (eq? left 'nil) (eq? right 'nil)))
(append (internals left) (internals right) (list (list (car tree) 'nil 'nil)))
'()))))
P62B (*) Collect the nodes at a given level in a list
A node of a binary tree is at level N if the path from the root to the node has length N-1.
The root node is at level 1. Write a predicate atlevel/3 to collect all nodes at a given level in a list.
% atlevel(T,L,S) :- S is the list of nodes of the binary tree T at level L
Using atlevel/3 it is easy to construct a predicate levelorder/2 which creates the level-order sequence
of the nodes. However, there are more efficient ways to do that.
(define (atlevel tree l)
(define (iter tree cur-l)
(cond [(eq? tree 'nil) '()]
[(= l cur-l) (list (list (car tree) 'nil 'nil))]
[else (append (iter (cadr tree) (+ cur-l 1)) (iter (caddr tree) (+ cur-l 1)))]))
(iter tree 1))
;广度优先
(define (levelorder tree)
(define (travel travel-que result)
(if (null? travel-que) result
(let ([mid-result
(foldr (lambda (x acc)
(if (not (eq? x 'nil))
(list (cons (cadr x) (cons (caddr x) (car acc)))
(cons (car x) (cadr acc)))
acc)) '(()()) travel-que)])
(append result (travel (car mid-result) (cadr mid-result))))))
(travel (list tree) '()))
P63 () Construct a complete binary tree
A complete binary tree with height H is defined as follows: The levels 1,2,3,...,H-1 contain the maximum number of nodes
(i.e 2(i-1) at the level i, note that we start counting the levels from 1 at the root).
In level H, which may contain less than the maximum possible number of nodes, all the nodes are "left-adjusted".
This means that in a levelorder tree traversal all internal nodes come first, the leaves come second, and empty successors
(the nil's which are not really nodes!) come last.
Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.
We can assign an address number to each node in a complete binary tree by enumerating the nodes in levelorder,
starting at the root with number 1. In doing so, we realize that for every node X with address A the following property holds:
The address of X's left and right successors are 2A and 2A+1, respectively, supposed the successors do exist.
This fact can be used to elegantly construct a complete binary tree structure. Write a predicate complete-binary-tree/2 with the following specification:
% complete-binary-tree(N,T) :- T is a complete binary tree with N nodes. (+,?)
Test your predicate in an appropriate way.
(define (height tree)
(if (or (null? tree) (eq? tree 'nil)) 0
(+ 1 (max (height (cadr tree)) (height (caddr tree))))))
;判断一棵树是否满二叉树
(define (full-binary-tree? tree)
(= (countNode tree) (maxNodes (height tree))))
;添加子节点规则
;1) 左右子树节点数量一致往左
;2) 左子树非满往左
;3) 其它情况往右
(define (addNode tree n)
(if (or (null? tree) (eq? tree 'nil)) (list n 'nil 'nil)
(let ([left-full (full-binary-tree? (cadr tree))]
[left-size (countNode (cadr tree))]
[right-size (countNode (caddr tree))])
(if (or (= left-size right-size) (not left-full))
(list (car tree) (addNode (cadr tree) n) (caddr tree))
(list (car tree) (cadr tree) (addNode (caddr tree) n))))));往右子树
(define (complete-binary-tree n)
(foldl (lambda (acc x)
(addNode acc x)) '() (range 1 n)))
;一棵树是完全二叉树的条件
;1) 满二叉树
;2) 左子树是高度为h-1的完全二叉树且右子树是高度为h-2的满二叉树
;3) 左子树是高度为h-1的满二叉树,且右子树是高度为h-1的完全二叉树
(define (complete-binary-tree? tree)
(if (full-binary-tree? tree) #t
(let ([h (height tree)]
[h-left (height (cadr tree))]
[h-right (height (caddr tree))])
(cond [(and (= h-left (- h 1)) (complete-binary-tree? (cadr tree));左子树是高度为h-1的完全二叉树
(= h-right (- h 2)) (full-binary-tree? (caddr tree))) #t];右子树是高度为h-2的满二叉树
[(and (= h-left (- h 1)) (full-binary-tree? (cadr tree));左子树是高度为h-1的满二叉树
(= h-right (- h 1)) (complete-binary-tree? (caddr tree))) #t];右子树是高度为h-1的完全二叉树
[else #f]))))
P64 (**) Layout a binary tree (1)
(W,X,Y,L,R) represents a (non-empty) binary tree with root W "positioned" at (X,Y), and subtrees L and R
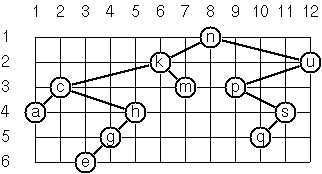
(define (layout-binary-tree tree)
(define (layout tree h order)
(if (eq? tree 'nil) 'nil
(let* ([layout-left (layout (cadr tree) (+ h 1) order)]
[self-order (if (eq? layout-left 'nil) order (+ (car layout-left) 1))]
[layout-right (layout (caddr tree) (+ h 1) (+ self-order 1))]
[maxorder (if (eq? layout-right 'nil) self-order (car layout-right))])
(list maxorder (car tree) self-order h
(if (eq? layout-left 'nil ) 'nil (cdr layout-left))
(if (eq? layout-right 'nil) 'nil (cdr layout-right))))))
(cdr (layout tree 0 1 )))
P65 (**) Layout a binary tree (2)
An alternative layout method is depicted in the illustration opposite. Find out the rules and write the corresponding Prolog predicate.
Hint: On a given level, the horizontal distance between neighboring nodes is constant.
Use the same conventions as in problem P64 and test your predicate in an appropriate way.
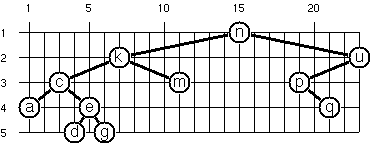
;最低一层子节点与父节点横坐标差为1,次低层为2,次次低层为4依次类推
(define (layout-binary-tree2 tree)
(define maxhight (height tree))
(define hightdelta (append (foldl (lambda (acc x) (cons (exponent 2 x) acc)) '() (range 0 (- maxhight 2))) '(0)));层级横坐标数组
;layout,如果c为0,表示当前节点的x坐标值尚未确定,需要根据layout-left来确定
(define (layout tree h c)
(if (eq? tree 'nil) 'nil
(let* ([layout-left (layout (cadr tree) (+ h 1) (if (> c 0) (- c (element-at hightdelta (+ h 1))) c))]
[self-c (cond [(= 0 c)
(if (eq? layout-left 'nil) 1
(+ (car layout-left) (element-at hightdelta (+ h 1))))]
[else c])]
[layout-right (layout (caddr tree) (+ h 1) (+ self-c (element-at hightdelta (+ h 1))))])
(list self-c (car tree) self-c h
(if (eq? layout-left 'nil ) 'nil (cdr layout-left))
(if (eq? layout-right 'nil) 'nil (cdr layout-right))))))
(cdr (layout tree 0 0)))
;测试用例
;(layout-binary-tree2 '(k (c (a nil nil) (e (d nil nil) (g nil nil))) (m nil nil)))
;(layout-binary-tree2 '(c (a nil nil) (e (d nil nil) (g nil nil))))
;(layout-binary-tree2 '(n (k (c (a nil nil) (e (d nil nil) (g nil nil))) (m nil nil)) (u (p nil (q nil nil)) nil)))
P66 (***) Layout a binary tree (3)
Yet another layout strategy is shown in the illustration opposite. The method yields a very compact layout while
maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate.
Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together
two subtrees to construct the combined binary tree?
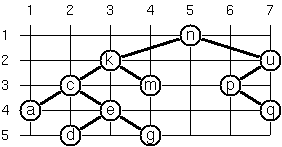
Use the same conventions as in problem P64 and P65 and test your predicate in an appropriate way.
Note: This is a difficult problem. Don't give up too early!
Which layout do you like most?
;1) 如果有左子树和右子树 根节点 = (右子树-左子树)/2 + 左子树
;2) 如果有左子树 根节点 = 左子树 + 1
;3) 如果有右子树 根节点 = c
(define (layout-binary-tree3 tree)
;用于检测一个节点是否与已经就位的节点产生冲突
(define (check-collision trees x y)
(define (match? tree exit)
(if (eq? 'nil tree) 'nil
(begin
(if (and (eq? x (cadr tree)) (eq? y (caddr tree))) (exit x))
(match? (cadddr tree) exit)
(match? (car (cddddr tree)) exit))))
(define (iter xs exit)
(if (null? xs) 'nil
(begin (match? (car xs) exit)
(iter (cdr xs) exit))))
(call/cc (lambda (exit) (iter trees exit))))
;用于将子树中所有节点x坐标移动2个位置
(define (shift tree)
(if (eq? 'nil tree) 'nil
(list (car tree) (+ 2 (cadr tree)) (caddr tree) (shift (cadddr tree)) (shift (car (cddddr tree))))))
(define (layout tree h c siblings)
(if (eq? tree 'nil) 'nil
(let* ([layout-left (layout (cadr tree) (+ h 1) (if (> c 1) (- c 1) c) siblings)]
[left-c (if (eq? 'nil layout-left) c (cadr layout-left))]
[layout-right (layout (caddr tree) (+ h 1) (if (eq? 'nil layout-left) (+ 1 left-c) (+ 2 left-c)) (cons layout-left siblings))]
[right-c (if (eq? 'nil layout-right) c (cadr layout-right))]
[self-c (if (and (not (eq? 'nil layout-left)) (not (eq? 'nil layout-right))) (+ (/ (- right-c left-c) 2) left-c)
(if (eq? 'nil layout-left) c (+ left-c 1)))]
[self-h (+ h 1)])
(if (not (eq? 'nil (check-collision siblings self-c self-h)))
;如果当前节点与已经就位的节点位置产生冲突,则对它的左右子树都调用shift
(list (car tree) (+ self-c 2) self-h (shift layout-left) (shift layout-right))
(list (car tree) self-c self-h layout-left layout-right)))))
(layout tree 0 1 '()))
;测试用例
;(layout-binary-tree3 '(k (c (a nil nil) (e (d nil nil) (g nil nil))) (m nil nil)))
;(layout-binary-tree3 '(c (a nil nil) (e (d nil nil) (g nil nil))))
;(layout-binary-tree3 '(n (k (c (a nil nil) (e (d nil nil) (g nil nil))) (m nil nil)) (u (p nil (q nil nil)) nil)))
;(layout-binary-tree3 '(a (b nil (c nil nil)) nil))
P67 (**) A string representation of binary trees
Somebody represents binary trees as strings of the following type (see example opposite):
a(b(d,e),c(,f(g,)))
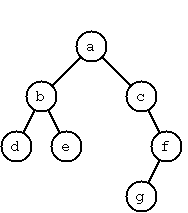
a) Write a Prolog predicate which generates this string representation, if the tree is given as usual (as nil or t(X,L,R) term).
Then write a predicate which does this inverse; i.e. given the string representation, construct the tree in the usual form. Finally,
combine the two predicates in a single predicate tree-string/2 which can be used in both directions.
b) Write the same predicate tree-string/2 using difference lists and a single predicate tree-dlist/2 which does the conversion
between a tree and a difference list in both directions.
For simplicity, suppose the information in the nodes is a single letter and there are no spaces in the string.
(define (tree->string tree)
(if (eq? 'nil tree) ""
(let* ([node (car tree)]
[left (cadr tree)]
[right (caddr tree)])
(if (and (eq? 'nil left) (eq? 'nil right)) node
(string-append node "(" (tree->string left) "," (tree->string right) ")")))))
;(tree->string '("a" ("b" ("d" nil nil) ("e" nil nil)) ("c" nil ("f" ("g" nil nil) nil))))
(define (string->tree str)
(define (string-split s)
(define (mysubstring s start end)
(cond [(eq? 0 end) ""]
[(eq? (string-length s) start) ""]
[else (substring s start end)]))
(define (find-split-index meet-l-bracket meet-r-bracket idx exit)
(let ([c (string-ref s idx)])
(cond [(eq? c #\,)
(if (or (not meet-l-bracket) meet-r-bracket) (exit idx)
(find-split-index meet-l-bracket meet-r-bracket (+ idx 1) exit))]
[(eq? c #\() (find-split-index #t meet-r-bracket (+ idx 1) exit)]
[(eq? c #\)) (find-split-index meet-l-bracket #t (+ idx 1) exit)]
[else (find-split-index meet-l-bracket meet-r-bracket (+ idx 1) exit)]
)))
;(string-split "b(d,e),c(,f(g,))")
;=>("b(d,e)" "c(,f(g,))")
(let* ([idx (call/cc (lambda (exit) (find-split-index #f #f 0 exit)))]
[fst (mysubstring s 0 idx)]
[snd (mysubstring s (+ idx 1) (string-length s))])
(list fst snd)))
(cond [(string=? str "") 'nil]
[(eq? (string-length str) 1) (list str 'nil 'nil)]
[else (let* ([node (substring str 0 1)]
[splitstr (string-split (substring str 2 (- (string-length str) 1)))]
[left-str (car splitstr)]
[right-str(cadr splitstr)])
(list node (string->tree left-str) (string->tree right-str)))]))
;(string->tree "a(b(d,e),c(,f(g,)))")
(define (tree<->string input)
(cond [(string? input) (string->tree input)]
[(list? input) (tree->string input)]
[else 'nil]))
P68 (**) Preorder and inorder sequences of binary trees
We consider binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67.
a) Write predicates preorder/2 and inorder/2 that construct the preorder and inorder sequence of a given binary tree,
respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in problem P67.
b) Can you use preorder/2 from problem part a) in the reverse direction; i.e. given a preorder sequence, construct a
corresponding tree? If not, make the necessary arrangements.
c) If both the preorder sequence and the inorder sequence of the nodes of a binary tree are given, then the tree is
determined unambiguously. Write a predicate pre-in-tree/3 that does the job.
d) Solve problems a) to c) using difference lists. Cool! Use the predefined predicate time/1 to compare the solutions.
What happens if the same character appears in more than one node. Try for instance pre-in-tree(aba,baa,T).
(define (preorder tree)
(if (eq? tree 'nil) ""
(string-append (car tree) (preorder (cadr tree)) (preorder (caddr tree)))))
;(preorder '("a" ("b" ("d" nil nil) ("e" nil nil)) ("c" nil ("f" ("g" nil nil) nil))))
(define (inorder tree)
(if (eq? tree 'nil) ""
(string-append (inorder (cadr tree)) (car tree) (inorder (caddr tree)))))
;(inorder '("a" ("b" ("d" nil nil) ("e" nil nil)) ("c" nil ("f" ("g" nil nil) nil))))
;input: preorder sequence
;output: binary tree
;'abdecfg'
(define (build-preorder pre-str)
(let* ([len (string-length pre-str)]
[c (if (> len 0) (substring pre-str 0 1) "")])
(cond [(eq? len 0) '(nil nil)]
[(eq? len 1) (cons c (build-preorder ""))]
[(eq? len 2) (list c (build-preorder (substring pre-str 1 2)) 'nil)]
[else (list c
(build-preorder (substring pre-str 1 2))
(build-preorder (substring pre-str 2 len)))])))
;(build-preorder "abdecfg")
;1)寻找根节点,在in-str中寻找pre-str中的第一个元素,此元素即为根节点
;2)将in-str从分成两份例如"dbeacgf"-> "dbe" "cgf"
;3)将pre-str也分成对应数量的两份例如"abdecfg" -> "bde" "cfg"
;4)在两个子串上递归
(define (pre-in-tree pre-str in-str)
(define (mysubstring s start end)
(cond [(eq? 0 end) ""]
[(eq? (string-length s) start) ""]
[else (substring s start end)]))
(define (find-root c in-str idx exit)
(if (> idx (string-length in-str)) 'nil
(if (eq? c (string-ref in-str idx)) (exit idx)
(find-root c in-str (+ idx 1) exit))))
(let ([len-pre (string-length pre-str)]
[len-in (string-length in-str)])
(if (not (eq? len-pre len-in)) 'nil
(cond [(eq? 0 len-pre) 'nil]
[(eq? 1 len-pre) (list pre-str 'nil 'nil)]
[else (let ([root-idx (call/cc (lambda (exit) (find-root (string-ref pre-str 0) in-str 0 exit)))])
(if (eq? root-idx 'nil) 'nil
(let* ([root (substring pre-str 0 1)]
[sub-in1 (mysubstring in-str 0 root-idx)]
[sub-in2 (mysubstring in-str (+ root-idx 1) (string-length in-str))]
[sub-pre1 (mysubstring pre-str 1 (+ 1 (string-length sub-in1)))]
[sub-pre2 (mysubstring pre-str (+ 1 (string-length sub-in1)) (string-length pre-str))])
(list root (pre-in-tree sub-pre1 sub-in1)
(pre-in-tree sub-pre2 sub-in2)))))]))))
;(pre-in-tree "abdecfg" "dbeacgf")
P69 (**) Dotstring representation of binary trees
We consider again binary trees with nodes that are identified by single lower-case letters,
as in the example of problem P67. Such a tree can be represented by the preorder sequence of its
nodes in which dots (.) are inserted where an empty subtree (nil) is encountered during the tree traversal.
For example, the tree shown in problem P67 is represented as 'abd..e..c.fg...'.
First, try to establish a syntax (BNF or syntax diagrams) and then write a predicate tree-dotstring/2 which
does the conversion in both directions. Use difference lists.
(define (tree->dotstring tree)
(if (eq? tree 'nil) "."
(string-append (car tree) (tree->dotstring (cadr tree)) (tree->dotstring (caddr tree)))))
;(tree-dotstring '("a" ("b" ("d" nil nil) ("e" nil nil)) ("c" nil ("f" ("g" nil nil) nil))))
(define (dotstring->tree dotstr)
(define (process dotstr)
(let ([c (substring dotstr 0 1)])
(if (string=? "." c) (list (substring dotstr 1 (string-length dotstr)) 'nil)
(let* ([left (process (substring dotstr 1 (string-length dotstr)))]
[right (process (car left))])
(list (car right) (list c (cadr left) (cadr right)))))))
(cadr (process dotstr)))
;(dotstring->tree "abd..e..c.fg...")



