python爬虫

一、用python爬取一个求职网页的一些信息

网页截图如下：

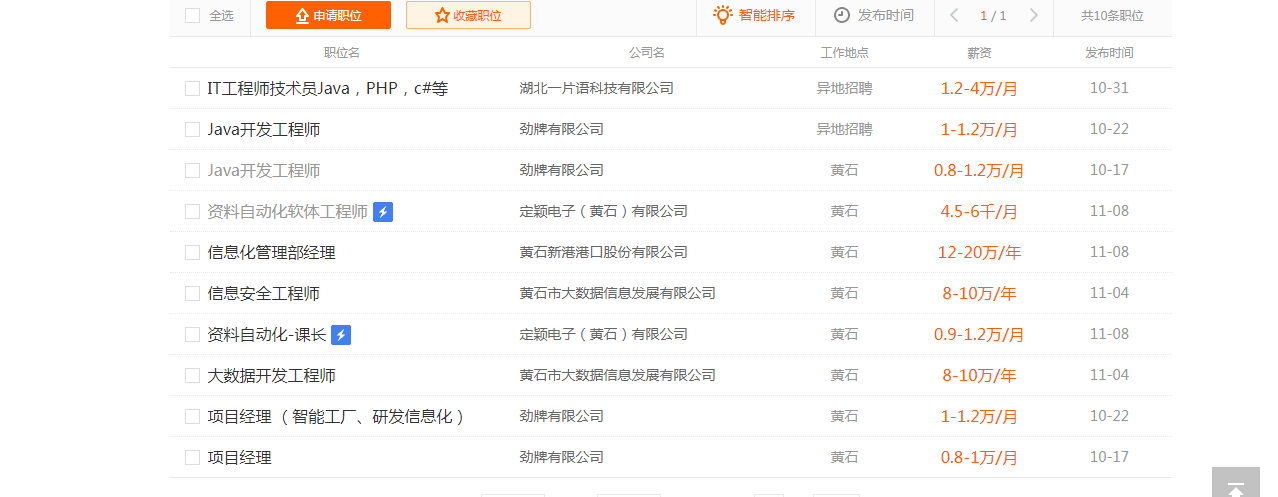
代码：

import requests
from bs4 import BeautifulSoup
import io
import sys
sys.stdout=io.TextIOWrapper(sys.stdout.buffer,encoding='gb18030')
headers={ "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/70.0.3538.110 Safari/537.36"}
r=requests.get('https://search.51job.com/list/180400,000000,0000,00,9,99,java,2,1.html?lang=c&stype=1&postchannel=0000&workyear=99&cotype=99&degreefrom=99&jobterm=99&companysize=99&lonlat=0%2C0&radius=-1&ord_field=0&confirmdate=9&fromType=&dibiaoid=0&address=&line=&specialarea=00&from=&welfare=')

r.encoding=r.apparent_encoding
result=r.text
bs=BeautifulSoup(result,'html.parser')

li=bs.find_all('p',attrs={'class':'t1'})
for l in li:
    print(l.text)
li1=bs.find_all('span',attrs={'class':'t2'})
for m in li1:
    print(m.text)
li2=bs.find_all('span',attrs={'class':'t3'})
for n in li2:
    print(n.text)
li3=bs.find_all('span',attrs={'class':'t4'})
for a in li3:
    print(a.text)
li4=bs.find_all('span',attrs={'class':'t5'})
for b in li4:
    print(b.text)

结果：

二、python代码

算24

描述

　　给出4个小于10的正整数，可以使用加、减、乘、除4种运算以及括号把4个数连接起来得到一个表达式。现在问题是，是否存在一种方式使得所得表达式的结果等于24。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬

这里加、减、乘、除以及括号的运算结果和运算优先级跟平常定义一致。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬

　　例如，对于5，5，5，1，可知5×（5－1／5）＝24。又如，对于1，1，4，2无论如何都不能得到24。

1.

from itertools import permutations
n1 = input("")
n2 = input("")
n3 = input("")
n4 = input("")
n = n1+n2+n3+n4
sum = 1
for i in n:
    sum *= eval(i)
if sum < 24:
    print("NO")
    exit()
notation = ['+', '-', '*', "/"]
st = set()
num = 0
number = set(permutations(n))
for i in notation:
    s = i
    t1 = notation.copy()
    t1.remove(i)
    for j in t1:
        s += j
        t2 = t1.copy()
        t2.remove(j)
        for p in t2:
            s += p
            st.add(s)
            s = i+j
        s = i
newst = set()
for i in number:
    for j in st:
        newst.add(i[0]+j[0]+i[1]+j[1]+i[2]+j[2]+i[3])
# print(newst)
all = set()
for i in newst:
    i1 = '('+i[0:3]+')'+i[3:]
    i2 = i[0:2]+'('+i[2:5]+')'+i[5:]
    i3 = i[0:4] + '(' + i[4:] + ')'
    i4 = '(('+i[0:3]+')'+i[3:5]+")"+i[5:]
    i5 = i[0:2]+'(('+i[2:5]+')'+i[5:]+")"
    i6 = '(' + i[0:2] + '(' + i[2:5] + '))' + i[5:]
    i7 = i[0:2]+'('+i[2:4]+'('+i[4:]+"))"
    all.add(i1)
    all.add(i2)
    all.add(i3)
    all.add(i4)
    all.add(i5)
    all.add(i6)
    all.add(i7)
result = []
for i in all:
    try:
        if eval(i) == 24:
          result.append(i)
    except:
        pass
print("YES")
print("("+sorted(result)[0]+")")

2.

import itertools

def twentyfour(cards):
    '''史上最短计算24点代码'''
    for nums in itertools.permutations(cards): # 四个数
        for ops in itertools.product('+-*/', repeat=3): # 三个运算符（可重复！）
            # 构造三种中缀表达式 (bsd)
            bds1 = '(({0}{4}{1}){5}({2}{6}{3}))'.format(*nums, *ops)  # (a+b)*(c-d)
            bds2 = '((({0}{4}{1}){5}{2}){6}{3})'.format(*nums, *ops)  # (a+b)*c-d
            bds3 = '(({0}{4}({1}{5}{2})){6}{3})'.format(*nums, *ops)  #  a/(b-(c/d))
            
            for bds in [bds1, bds2, bds3]: # 遍历
                try:
                    if abs(eval(bds) - 24.0) < 1e-10:   # eval函数
                        print("YES")
                        return bds
                except ZeroDivisionError: # 零除错误！
                    continue
    
    return 'NO'
    

cards=[[5,5,5,1]]
for card in cards:
    print(twentyfour(card))

二分法求平方根

描述

设计一个用二分法计算一个大于或等于 1 的实数 n 的平方根的函数sqrt_binary(n)，计算精度控制在计算结果的平方与输入的误差不大于1e-6。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬

注：初始区间取[0,n]

import math

def sqrt_biary(n):
    low=0   #设置下限为0
    high=max(n,1)   #设置上限为n和1之中的最大数，即：如果n>=1，那么上限为n；如果n<1，那么上限为1
    guess=(low+high)/2   #先从中间值开始猜
    count=1   #设置猜测次数起始值为1
    while abs(guess**2-n)>(1e-6) and count<100: #当猜测值的平方和n本身的差值无限接近误差值时，循环才会停止；同时设置猜测次数不超过100次
        if guess**2<n:  #如果猜测值的平方小于n，那么将此设为下限
            low=guess
        else:           #如果猜测值的平方大于n，那么将此设为上限
            high=guess
        guess=(low+high)/2  #根据新的上下限，重新进行猜测
        count+=1    #猜测次数每次增加1
    print(guess) 


m=float(input())
sqrt_biary(m)
print(math.sqrt(m))