粗糙集理论
粗糙集理论
1 粗糙集的基本概念
在粗糙集理论中,我们把知识看做是一种能被用于分类对象的能力。其中对象可以代表现实世界中的任意事物,包括物品、属性、概念等。即:知识需要同现实世界中特定环境的确定对象相关联,这一集合称为论域。
知识与概念
令U为包含若干对象的非空有限集,也即论域,在论域中,称任意集合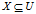 为一个概念或范畴。特别地,我们把空集也视为一个概念,称之为空概念。而由任意个这样的X组成的子集簇形成了U中抽象知识,简称为知识。
为一个概念或范畴。特别地,我们把空集也视为一个概念,称之为空概念。而由任意个这样的X组成的子集簇形成了U中抽象知识,简称为知识。
知识库
在给定论域中,任意选择一个等价关系集R,我们可以得到一个二元组K=<U,R>,称这样的二元组视为一个知识库(近似空间)。
在论域中,任何等价关系都能导出一个对论域的划分,从而形成了一个知识库。由此,每个知识库就能够与论域中的某个等价类一一对应。
不可分辨(不可区分/不分明)关系
在给定的论域U上,任意选择一个等价关系集R和R的子集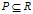 ,且
,且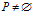 ,则P中所有等价关系的交集依然是论域U中的等价关系,称该等价关系为P的不可分辨关系,记作IND(P)。并且
,则P中所有等价关系的交集依然是论域U中的等价关系,称该等价关系为P的不可分辨关系,记作IND(P)。并且

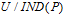 :表示非空子族集
:表示非空子族集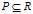 所产生的不分明关系IND(P)的所有等价类关系的集合,又称该知识为知识库K=<U,R>中关于P-基本知识(P-基本集)
所产生的不分明关系IND(P)的所有等价类关系的集合,又称该知识为知识库K=<U,R>中关于P-基本知识(P-基本集)
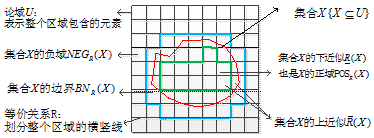
集合的上下近似
上近似包含了所有那些可能是属于X的元素,下近似包含了所有使用知识R可确切分类到X的元素。在给定的知识库K=<U,R>中,任意选择集合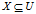 ,可以定于X关于知识R的上下近似。
,可以定于X关于知识R的上下近似。
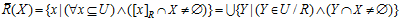
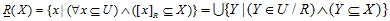
概念的边界域由不能肯定分类到这个概念或其补集中的所有元素组成。
在给定的知识库K=<U,R>上,存在着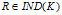 ,可以用于说明系统的特征,称之为系统参数。对于任意集合
,可以用于说明系统的特征,称之为系统参数。对于任意集合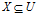 ,我们可以得到X相对于这个系统参数R所提供的信息的数量的多少,称这个数量为X的重要度。
,我们可以得到X相对于这个系统参数R所提供的信息的数量的多少,称这个数量为X的重要度。
(4)随着X相对于R的重要度的增加,使用集合X表示系统参数R的程度也会增加。
在给定的知识库K=<U,R>中,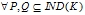 ,定义
,定义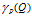 为知识Q对于知识P的依赖程度。
为知识Q对于知识P的依赖程度。 即Q的P的正域,其中包含了论域U的信息中能够按照P进行分类后能够被唯一的划分到Q的等价类中的那一部分。
即Q的P的正域,其中包含了论域U的信息中能够按照P进行分类后能够被唯一的划分到Q的等价类中的那一部分。
(2)如果 =1,表示在P中包含了Q的全部信息,Q对P的依赖程度为完全依赖。
=1,表示在P中包含了Q的全部信息,Q对P的依赖程度为完全依赖。
(3)如果 =0,表示在P中完全不包含Q的信息,Q与P是完全独立的。
=0,表示在P中完全不包含Q的信息,Q与P是完全独立的。
(4)如果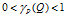 ,那么P中仅包含Q的部分信息,也可以说Q存在着对P的程度为k的依赖关系。
,那么P中仅包含Q的部分信息,也可以说Q存在着对P的程度为k的依赖关系。
在K=<U,R>中,对于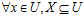 ,则定义为元素x关于知识R的隶属于集合的粗糙隶属度,也称为集合X的R-粗糙隶属函数。
,则定义为元素x关于知识R的隶属于集合的粗糙隶属度,也称为集合X的R-粗糙隶属函数。

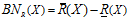
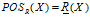
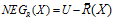
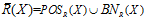

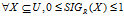 。
。
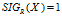 ,那么使用集合X可以完全表示系统参数R。
,那么使用集合X可以完全表示系统参数R。
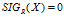 ,那么使用集合X完全不能表示系统参数R。
,那么使用集合X完全不能表示系统参数R。
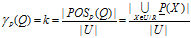
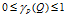
 。而粗糙集理论中,
。而粗糙集理论中,
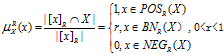

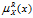 值越大说明对象
值越大说明对象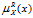 =1,表示对象x依赖知识R判断肯定属于集合X。
=1,表示对象x依赖知识R判断肯定属于集合X。
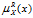 =0,表示对象x依赖知识R判断肯定不属于集合X。
=0,表示对象x依赖知识R判断肯定不属于集合X。
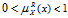 ,表明对象x依据知识R有可能属于集合X,同时也有可能不属于集合X。
,表明对象x依据知识R有可能属于集合X,同时也有可能不属于集合X。
