LDA
LDA
1 概述
LDA主题模型是一个包含词汇、主题(隐变量)、文档的三层结构,把文档集中的文档看做是多个主题信息的混合分布,每个主题看做是对应预料库中所有词汇上的混合分布。
LDA主题模型生成文档语料库的过程如下:(建设生成的语料库包含m篇文档、K个主题)
(1)对于m篇文档,生成"文档-主题"分布。文档主题分布也是一个多项式分布,它的参数服从参数为 的Dirichlet先验分布。(Dirichlet(狄立克雷),Beta分布的多元推广)。
的Dirichlet先验分布。(Dirichlet(狄立克雷),Beta分布的多元推广)。
(2)获取每个主题下的"主题-词汇"的分布。主题-词汇分布是一个多项式分布,且它的参数变量服从参数为 的Dirichlet先验分布。
的Dirichlet先验分布。
(3)根据 "文档-主题"、"主题-词汇"分布,依次生成所有文档中的词汇。具体做法,首先根据该文档的"文档-主题"分布规律采样一个主题,然后从这个主题对应的"主题-词汇"分布规律中采样生成一个词汇,不断重复步骤3的生成过程,直到m篇文档词汇全部生成。(采用Gibbs采样法,一种特殊的MCMC(Markov chain Monte Carlo 马尔可夫链蒙特卡罗)算法)
2 LDA模型
LDA主题模型生成文档语料库的过程可以画成一个经典的贝叶斯网络图:
(1)  是每个文档下主题的多项式分布的Dirichlet先验参数,
是每个文档下主题的多项式分布的Dirichlet先验参数, 是每个主题下词的多项式分布的Dirichlet先验参数。
是每个主题下词的多项式分布的Dirichlet先验参数。
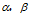 一般事先给定,如果取0,1对称的Dirichlet分布,表示在参数学习接收后,期望每篇文档的主题不会十分集中。
一般事先给定,如果取0,1对称的Dirichlet分布,表示在参数学习接收后,期望每篇文档的主题不会十分集中。
(2) 表示第m个文档下的主题分布的分布;
表示第m个文档下的主题分布的分布; 表示第k个主题下的词分布。
表示第k个主题下的词分布。
对于第i篇文档 的主题分布是
的主题分布是 ,是长度为K的向量;对于第i篇文档的
,是长度为K的向量;对于第i篇文档的 ,在主题分布
,在主题分布 下,可以确定一个具体的主题
下,可以确定一个具体的主题 对于第K个主题
对于第K个主题 的词分布
的词分布 ,是长度为v的向量;
,是长度为v的向量;
(3) 是第m个文档的单词总数。
是第m个文档的单词总数。 是第m个文档中第n个词的主题,
是第m个文档中第n个词的主题,
Gibbs迭代规则的思想:即不考虑当前词汇的主题分配,据此词汇所在文档的主题分布以及各个主题下词汇分布来计算此词汇被分配到各个主题的概率分布,然后选择以最大概率被分配的主题。
(1) 表示排除当前第i个词汇,根据文档集中其他词汇序列的主题分布来计算第i个词汇属于第k个主题的概率
表示排除当前第i个词汇,根据文档集中其他词汇序列的主题分布来计算第i个词汇属于第k个主题的概率
3)t 是第i个词汇对应词汇的字典序列号, 表示排除当前词汇,k个主题中词汇 t 出现次数。
表示排除当前词汇,k个主题中词汇 t 出现次数。
4)m 是当前词汇出现在第 m 篇文档中, 表示排除当前词汇,m 篇文档中出现词汇k的次数。
表示排除当前词汇,m 篇文档中出现词汇k的次数。
当 Gibbs 采样收敛后,跟据每个文档中主题分配次数以及每个主题中词汇分配次数来计算"文档-主题"分布和和"主题-词汇"分布。
1) 表示标号为v的词语分配到主题 k 的次数,
表示标号为v的词语分配到主题 k 的次数, 表示文档m 中所有词语分配到主题 z 的个数。
表示文档m 中所有词语分配到主题 z 的个数。
贝塔分布中的参数可以理解为伪计数,伯努利分布的似然函数可以表示为,表示一次事件发生的概率,它为贝塔有相同的形式,因此可以用贝塔分布作为其先验分布。
在刚才例子的后验概率的最终表达式中,参数α、β和x一起作为参数θ的指数——后验概率的参数为(x+α,1-x+β)。而这个指数的实践意义是:投币过程中,正面朝上的次数。α和β 先验性的给出了在没有任何实验的前提下,硬币朝上的概率分配;因此,α和β可被称作"伪计数"。
Dirichleet分布其实就是Beta分布推广到K维的情况。
而Beta分布的一个重要应该是作为伯努利分布和二项式分布的共轭先验分布出现,在机器学习和数理统计学中有重要应用。
二项分布的共轭先验分布是Beta分布,那多项分布的共轭先验分布就是Dirichleet分布。
后验概率分布拥有与先验分布相同的函数形式。这个性质被叫做共轭性。共轭先验有着很重要的作⽤。它使得后验概率分布的函数形式与先验概率相同,因此使得贝叶斯分析得到了极⼤的简化。
如果一个文档中只有两个词,那这个文档就是个二项分布吧, 但一个文档中一般有很多词,比如有K个,所以说文档是K项分布吧。
注意:词频不是Dirichleet分布,词频是K项分布,而K项分布需要有参数的,这个参数是Dirichleet分布
[1] 边晋强. 基于LDA主题模型的文档文摘研究[D].北京理工大学,2015.
[2] http://blog.csdn.net/xueyingxue001/article/details/52396279?locationNum=1&fps=1


 选择
选择 ,表示由词分布
,表示由词分布 确定词,即得到观测值
确定词,即得到观测值 。
。

 ;
;
 ,由
,由 个词汇组成,可重复;
个词汇组成,可重复;
 是第m个文档中的第n个词。
是第m个文档中的第n个词。
 :文档m中第n个词在词典中的序号,属于1到V
:文档m中第n个词在词典中的序号,属于1到V
 :文档m第n个词汇的主题标号,属于1到k
:文档m第n个词汇的主题标号,属于1到k
 k:第k个主题的词汇分布中的参数向量
k:第k个主题的词汇分布中的参数向量
 :第m文档的主题分布中的参数向量
:第m文档的主题分布中的参数向量


 是Dirichlet
是Dirichlet 分布的
分布的





 是主题在词汇上分布,式(2-10)中分子的意义是字典中第 t 个词汇分配到主题k下的次数,分母是表示的意义字典中所有词汇被分配到主题k下的次数,
是主题在词汇上分布,式(2-10)中分子的意义是字典中第 t 个词汇分配到主题k下的次数,分母是表示的意义字典中所有词汇被分配到主题k下的次数, 是主题-词汇分布中的先验参数,表示人为认为词汇 t 被分配到主题 k 的次数。所有词汇初始时都是等可能的被分配,以这里都假定
是主题-词汇分布中的先验参数,表示人为认为词汇 t 被分配到主题 k 的次数。所有词汇初始时都是等可能的被分配,以这里都假定 =1。
=1。
 是文档-主题分布,式(2-11)中分子的意义是主题 k 被分配到第 m 篇文档中的次数,分母是表示的意义各个主题被分配到第 m 篇文档中的次数总和,文档m 的长度。
是文档-主题分布,式(2-11)中分子的意义是主题 k 被分配到第 m 篇文档中的次数,分母是表示的意义各个主题被分配到第 m 篇文档中的次数总和,文档m 的长度。 是文档-主题分布中的先验参数,表示主题 k 被分配的次数。所有主题初始时都是等可能的被分配,以这里都假定
是文档-主题分布中的先验参数,表示主题 k 被分配的次数。所有主题初始时都是等可能的被分配,以这里都假定 =1
=1


