支持向量机
支持向量机
1 概念
支持向量机是一种分类方法，通过寻求结构化、风险最小，来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较小的情况下，亦能获得良好统计规律的目的。通俗来讲，他是一种二类分类模型，基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。
SVM可以很好的应用于高维数据，避免维灾难问题。这种方法具有一个独特的特点，它使用训练实例的一个子集来表示决策边界，该子集作为支持向量。
尽管SVM的训练非常慢，但是由于其对复杂的非线性边界的建模能力，他们是非常准确的，与其他模型相比，它们不至于出现过分拟合的现象。
2 最大边缘超平面
具有较大边缘的决策边界比具有较小边缘的决策边界具有更好的泛化误差。直觉上，如果边缘比较小，决策边界任何轻微的扰动都可能对分类产生显著的影响。因此，那些决策边界边缘较小的分类器对模型的过分拟合更加敏感，从而在未知的样本上的泛化能力很差。
统计学理论给出了线性分类器边缘与其泛化误差之间关系的形式化解释，称之为SWM（structural risk minimization）结构风险最小化理论。该理论根据分类器的训练误差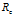
。训练样本数N和模型的复杂度h，给出了分类器的泛化误差的一个上界R。在概率
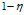下，分类器的泛化误差在最坏情况下满足
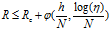
其中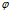
是能力的单调增函数。所以随着，能力的增加，泛化误差的上界也随之提高，因此需要设计一个最大化决策边界的边缘的线性分类器，以确保最坏情况下的泛化误差最小。线性SVM就是这样的分类器。
3 线性支持向量机：可分情况
线性SVM寻找具有最大边缘的超平面，因此它也经常被称为最大边缘分类器。为了理解SVM如何学习这样的边界，我们需要对线性分类器的决策边界和边缘进行讨论。
- 线性决策边界
一个包含N个训练样本的二类分类问题，每个样本表示为一个二元组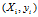
，其中
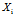表示第i个样本的属性集，
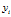表示它的类标号。一个线性分类器的决策边界可以写成：
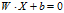
其中W和b是模型的参数。
对于任意位于决策边界上方的方块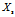
，我们可以证明
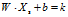，k>0。
对于任意位于决策边界下方的方块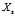
，我们可以证明
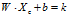，k<0。
于是可以用夏磊的方式预测任何测试样本Z的类标号。
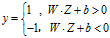
- 边缘
两个超平面上任意两个数据点的距离可以表示为
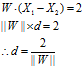
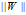表示范数，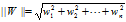
- SVM模型
最大边缘化等价于最小化下面的目标函数：
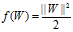
所以SVM的模型可以定义为：
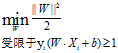
由于目标函数是二次的，而约束在参数W和b上是线性的，因此这个问题是一个凸函数优化问题。可以通过标准的拉个朗日乘子方法求解。
对应的拉格朗日函数为：
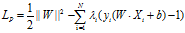
对于函数的优化问题设计到大量参数，为了简化问题，将问题换成对偶问题，对应的对偶拉格朗日函数为：
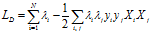
通过对偶函数找到对应的一组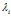
（可以通过二次规划），再通过
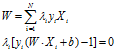，即可求得W和b。
决策边界可以表示成：
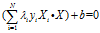
实践中，使用b的平均值作为决策边界的参数，它的大小取决于使用的支持向量。
4 线性支持向量机：不可分情况
数据线性可分是一种理想的状态，实际上，训练的数据是有噪声的，因此必须放松不等式的约束，以适应非线性可分数据。可以通过在优化问题的约束中引入正值的松弛变量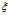
来实现。
修改后的最大边缘目标函数为：
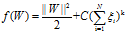
相应的拉格朗日函数为：
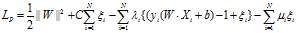
对偶的拉格朗日函数为：
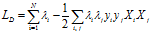
尽管线性可分与线性不可分的对偶的拉个朗日函数一样，但是拉格朗日乘子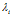
上的约束不同。
非线性的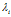
被限制在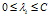
。
5 非线性支持向量机
很多真实生活中的数据集，决策面都是非线性的。为了解决分线性分割问题。假设存在一个合适的函数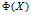
来变换给定的数据集，让数据集的分割问题映射到高维空间下，于是线性决策的边界具有以下形式：
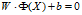
非线性支持向量的模型如下
最大边缘目标函数为：
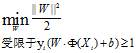
对偶的拉格朗日函数为：
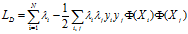
通过二次规划技术找到对应的一组，再通过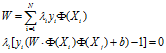
，即可求得W和b。
最后可以通过下式对检验的实例Z进行分类。
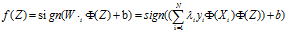
其中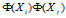
即相似度被称为核技术方法。
核技术
核技术使用中使用原属性集计算变换后的空间中的相似度的方法。该技术有利于处理如何实现非线性的问题。相似度函数K称为核函数，核函数必须满足Mercer定理。
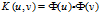
任何半正定的函数都可以作为核函数。当z*Mz > 0弱化为z*Mz≥0时，称M是半正定矩阵
参考文献：
