监督学习
监督学习
1 监督学习
在机器学习中，监督学习又被成为分类（Classfication）或者归纳学习（Inductive Learning）,这种类型的学习类似于人类学习的方式，从过去的经验中获取知识以用于提高解决现实问题的能力。监督学习在Web数据挖掘领域的一个成熟的应用是学习一个目标函数从而用于预测实例的类属性值。
给定一个数据集D，机器学习任务的目标就是产生一个联系属性值集合A和类标集合C的分类/预测函数，这个函数可以用于预测新的数据的类属性。这个函数通常被称为分裂模型、预测模型或者为分类器。这个分类模型的形式并不单一，例如决策树、规则集、贝叶斯模型或者一个超平面。
在监督学习中，我们通常把数据分为两个子集，一个子集作为训练集，一个子集作为测试集，测试集中样例往往也是带有类标的，通过检查模型预测的类标与实际类标是否一致，我们可以评测学习所得到模型的准确度。
2 决策树
决策树是一种监督式的学习方法，产生一种类似流程图的树结构。决策树对数据进行处理是利用归纳算法产生分类规则和决策树，再对新数据进行预测分类。决策树构建的主要步骤有三个：第一是选择适合的算法训练样本构建决策树，第二是适当的修剪决策树，第三是从决策树中萃取知识规则。决策树算法是一种贪心算法，包括Quinlan于1979年提出ID3算法，C4.5和C5.0算法是ID3算法的修订版本；Friedman等人提出的CART算法。
ID3算法是建立在奥卡姆剃刀原理的基础上的，越是小型的决策树越优于大的决策树。
C4.5算法是ID3算法的一种改进。其主要的改进在于用GainRatio来选择属性，克服了用信息增益选择属性时偏向于选择取值多的属性的不足；在树的构造过程中进行剪枝；能够完成对连续属性的离散化处理；能够对不完整数据进行处理。
C5.0算法则是C4.5算法的改进，适用于处理大数据集。主要改进是采用Boosting Tree来提高模型准确率。（boosting 是多棵决策树组合起来采用投票方式产生一个预测结果的方法机制来产生预测结果）。除此之外C5.0算法允许设定错误率最小的模型，依据不同的分类错误设定不同的成本。
CART,（Classification And Regression Tree）算法是基于树结构产生分类和回归模型的过程，是一种产生二元树的技术。最大的不同是其中每一个节点上都采用二分法。CART算法使用熵作为选择最好分割变量的测量准则。
2.1 决策树算法
决策树算法的框架
TreeGrowth(E,F)
If stopping_cond(E,F) = true then
//stopping_cond(E,F)检测是否搜有的记录都属于同一个类，或者都具 有相同的属性值，决定是否终止决策树的增长。
Leaf = createNode()
//为决策树建立新结点。决策树的节点分为2种，一种是类标号， 记为node.label;一种是测试节点，记为node.test_cond。
Leaf.label = Classify(E)
//Classify()为叶节点确定类标号。其中Clssify()返回的是最大化的p(i|t)的参数i，其中p(i|t)表示该节点上属于类i的训练记录所占的比例。
Return leaf
Else
Root = createNode()
Root.test_cond=find_best_split(E,F)
//find_best_split(E,F)用于确定应当选择哪个属性作为划分训练记录的测试条件。测试条件的选择取决于使用哪种不纯性度量来评估划分，常用的度量包括熵、Gini指数和
统计量。
令V={v|v是root.test_cond的一个可能的输出}
For 每个v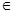
V do
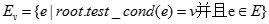
将child作为root的派生节点添加到树中，并将边（root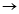
child）标为v
End for
End if
Return root
2.2 最佳的划分度量
- 信息增益
1）给定一个数据集，用熵计算D的混杂度，表示成entroPy(D)
算法C4.5即采用这种度量标准。信息增益基于熵，熵的计算公式
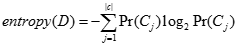
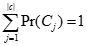
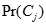表示
类中数据集D中的概率，即
类在D中的实例数目除以D中实际的总数。
- 然后，把所有属性都计算一遍，找出用那个属性来划分D可以将D的混杂度减少最多。设属性
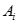可以取v个值，假定我们用
来划分D，则我们将D划分成v个不想交的子集
。然后划分后D的熵为
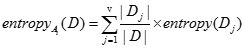
- 则属性
的信息增益计算如下
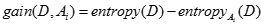
信息增益衡量混杂度的减少量。信息增益越大，作为根节点的可信度越高。
（2）信息增益率
信息增益率利用数据集的相对于属性值分布的熵归一化信息增益，用以修正上述偏袒性。
其中s是属性
的可能取值的数目，
是数据集中具有
属性第j个值的子集。通过计算，选择使得gainRatio值达到最大的属性来扩展决策树。
（3）基尼指数
基尼指数在CART中使用。基尼指数度量数据分区或训练元祖集D的不纯度，定义为：
其中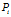
是D中元组属于
类的概率，并用|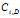
|/|D|估计。对m个类计算和。
当考虑二元划分时，计算每个结果分区的不纯度的加权和。例如，如果A的二元划分将D划分成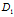
和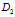
，则给定该划分，D的基尼指数为
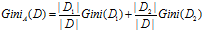
对于每个属性，考虑每种可能的二元划分。对于离散值属性，选择该属性产生最小基尼指数的子集作为它的分裂子集。
参考文献：
[1] http://www.cnblogs.com/biyeymyhjob/archive/2012/07/23/2605208.html
[2] http://blog.csdn.net/tianguokaka/article/details/9018933
