八皇后问题
核心算法描述:
DFS思想:(Depth-First-search)
DFS算法是一个递归算法,需要借助递归工作栈,空间复杂度为o(N)
从前往后寻找第i个皇后的列数,游标为j:
从前往后比较前i-1个皇后的位置是否与第i个皇后的位置冲突,游标为k:(k和i在图中表示行数):
如果:
(1) 列数冲突,即:第k个皇后的列数=第i个皇后的列数
(2) 正对角线冲突,即:第k个皇后的行数-第i个皇后的行数=第k个皇后的列数-第i个皇后的列数
如图所示:
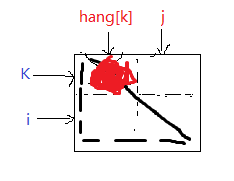
(3) 副对角线冲突,即第i个皇后的行数-第k个皇后的行数=第k个皇后的列数-第i个皇后的列数
如图所示:
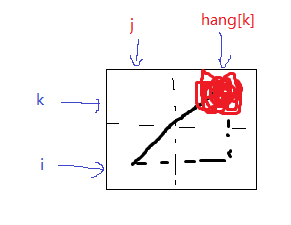
代码实现:
for (j=0; j<8; j++){ //将当前皇后i逐一尝试放置在不同的列
for(k=0; k<i; k++) //逐一判定i与前面的皇后是否冲突
if( hang[k] == j || (k - i) == (hang[k] - j) || (i - k) == (hang[k] - j )) break;
if (k == i) { //放置i,尝试第i+1个皇后
hang[i] = j;
queen(i + 1);
}
}
问题描述
会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上(有8 * 8个方格),使它们谁也不能被吃掉!这就是著名的八皇后问题。 对于某个满足要求的8皇后的摆放方法,定义一个皇后串a与之对应,即a=b1b2...b8,其中bi为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解(即92个不同的皇后串)。给出一个数b,要求输出第b个串。串的比较是这样的:皇后串x置于皇后串y之前,当且仅当将x视为整数时比y小。
输入数据
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数b(1 <= b <= 92)
输出要求
n行,每行输出对应一个输入。输出应是一个正整数,是对应于b的皇后串
输入样例
2
1
92
输出样例
15863724
84136275
Python实现1:
Q = [None for i in range(8)] VM = [False for i in range(8)] VL = [False for i in range(16)] VR = [False for i in range(16)] CNT = 0 N = 8 def dfs(cur): if cur == N: global CNT CNT += 1 else: for i in range(0, N): if not VM[i] and not VL[cur+i] and not VR[cur-i+N]: VM[i] = VL[cur+i] = VR[cur-i+N] = True Q[cur] = i dfs(cur+1) VM[i] = VL[cur+i] = VR[cur-i+N] = False dfs(0) print('ans = ' + str(CNT))
Python实现2:
def conflict(state,nextx): '定义冲突函数,state为元组,nextx为下一个皇后的水平位置,nexty为下一个皇后的垂直位置' nexty = len(state) for i in range(nexty): if abs(state[i]-nextx) in (0,nexty-i):#若下一个皇后和前面的皇后列相同或者在一条对角线上,则冲突 return True return False def queens(num,state=()):#num=n, '八皇后问题,这里num表示规模' for pos in range(num): if not conflict(state,pos):#位置不冲突 if len(state) == num - 1:#若是最后一个皇后,则返回该位置 yield (pos,) else:#若不是最后一个皇后,则将该位置返回到state元组并传给后面的皇后 for result in queens(num,state + (pos,)): yield (pos,) + result def prettyp(solution): '打印函数' def line(pos,length = len(solution)): '打印一行,皇后位置用X填充,其余用0填充' return 'O'*(pos)+'X'+'O'*(length-pos-1) for pos in solution: print(line(pos))
if __name__=='__main__': print(list(queens(4))
详解:
解题思路一
因为要求出92种不同摆放方法中的任意一种,所以我们不妨把92种不同的摆放方法一次性求出来,存放在一个数组里。为求解这道题我们需要有一个矩阵仿真棋盘,每次试放一个棋子时只能放在尚未被控制的格子上,一旦放置了一个新棋子,就在它所能控制的所有位置上设置标记,如此下去把八个棋子放好。当完成一种摆放时,就要尝试下一种。若要按照字典序将可行的摆放方法记录下来,就要按照一定的顺序进行尝试。也就是将第一个棋子按照从小到大的顺序尝试;对于第一个棋子的每一个位置,将第二个棋子从可行的位置从小到大的顺序尝试;在第一第二个棋子固定的情况下,将第三个棋子从可行的位置从小到大的顺序尝试;依次类推。
首先,我们有一个8*8的矩阵仿真棋盘标识当前已经摆放好的棋子所控制的区域。用一个有92行每行8个元素的二维数组记录可行的摆放方法。用一个递归程序来实现尝试摆放的过程。基本思想是假设我们将第一个棋子摆好,并设置了它所控制的区域,则这个问题变成了一个7皇后问题,用与8皇后同样的方法可以获得问题的解。那我们就把重心放在如何摆放一个皇后棋子上,摆放的基本步骤是:从第1到第8个位置,顺序地尝试将棋子放置在每一个未被控制的位置上,设置该棋子所控制的格子,将问题变为更小规模的问题向下递归,需要注意的是每次尝试一个新的未被控制的位置前,要将上一次尝试的位置所控制的格子复原。
参考程序一
#include <stdio.h> #include <math.h> int queenPlaces[92][8]; //存放92种皇后棋子的摆放方法 int count = 0; int board[8][8]; //仿真棋盘 void putQueen(int ithQueen); //递归函数,每次摆好一个棋子 void main() { int n, i, j; for(i = 0; i < 8; i++){ // 初始化 for(j = 0; j < 8; j++) board[i][j] = -1; for(j = 0; j < 92; j++) queenPlaces[j][i] = 0; } putQueen(0); //从第0个棋子开始摆放,运行的结果是将queenPlaces生成好 scanf("%d", &n); for(i = 0; i < n; i++){ int ith; scanf("%d", &ith); for(j = 0; j < 8; j++) printf("%d", queenPlaces[ith - 1][j]); printf("\n"); } } void putQueen(int ithQueen){ int i, k, r; if(ithQueen == 8){ count ++; return; } for(i = 0; i < 8; i++){ if(board[i][ithQueen] == -1){ //摆放皇后 board[i][ithQueen] = ithQueen; //将其后所有的摆放方法的第ith个皇后都放在i+1的位置上 //在i增加以后,后面的第ith个皇后摆放方法后覆盖此时的设置 for(k = count; k < 92; k++) queenPlaces[k][ithQueen] = i + 1; //设置控制范围 for(k = 0; k < 8; k++) for(r = 0; r < 8; r++) if(board[k][r] == -1 && (k == i || r == ithQueen || abs(k - i) == abs(r - ithQueen))) board[k][r] = ithQueen; //向下级递归 putQueen(ithQueen + 1); //回溯,撤销控制范围 for(k = 0; k < 8; k++) for(r = 0; r < 8; r++) if(board[k][r] == ithQueen) board[k][r] = -1; } } }
解题思路二
上面的方法用一个二维数组来记录棋盘被已经放置的棋子的控制情况,每次有新的棋子放置时用了枚举法来判断它控制的范围。还可以用三个一维数组来分别记录每一列,每个45度的斜线和每个135度的斜线上是否已经被已放置的棋子控制,这样每次有新的棋子放置时,不必再搜索它的控制范围,可以直接通过三个一维数组判断它是否与已经放置的棋子冲突,在不冲突的情况下,也可以通过分别设置三个一维数组的相应的值,来记录新棋子的控制范围。
参考程序二
#include <stdio.h> int record[92][9], mark[9], count = 0; //record记录全部解,mark记录当前解; bool range[9], line1[17], line2[17]; //分别记录列方向,45度,135度方向上被控制的情况 void tryToPut(int ); //求全部解的过程 void main() { int i, testtimes, num; scanf("%d", &testtimes); for(i = 0; i <=8; i++) range[i] = true; for(i = 0; i < 17; i ++) line1[i] = line2[i] = true; tryToPut(1); while(testtimes --){ scanf("%d", &num); for(i = 1; i <=8; i++) printf("%d", record[num - 1][i]); printf("\n"); } } void tryToPut(int i){ if(i > 8){ //如果最后一个皇后被放置完毕,将当前解复制到全部解中 for(int k = 1; k < 9; k ++) record[count][k] = mark[k]; count ++; } for(int j=1; j<=8; j++){ 逐一尝试将当前皇后放置在不同列上 if(range[j] && line1 [i + j] && line2[i - j + 9]){ //如果与前面的不冲突, //则把当前皇后放置在当前位置 mark[i] = j; range[j] = line1[i + j] = line2[i - j + 9] = false; tryToPut(i + 1); range[j] = line1[i + j] = line2[i - j + 9] = true; } } }
解题思路三
这个题目也可以不用仿真棋盘来模拟已放置棋子的控制区域,而只用一个有8个元素的数组记录已经摆放的棋子摆在什么位置,当要放置一个新的棋子时,只需要判断它与已经放置的棋子之间是否冲突就行了。
参考程序三
#include <stdio.h> int ans[92][8], n, b, i, j, num, hang[8]; void queen(int i){ int j, k; if(i == 8){ //一组新的解产生了 for(j = 0; j < 8; j++) ans[num][j] = hang[j] + 1; num++; return; } for (j=0; j<8; j++){ //将当前皇后i逐一尝试放置在不同的列 for(k=0; k<i; k++) //逐一判定i与前面的皇后是否冲突 if( hang[k] == j || (k - i) == (hang[k] - j) || (i - k) == (hang[k] - j )) break; if (k == i) { //放置i,尝试第i+1个皇后 hang[i] = j; queen(i + 1); } } } void main( ){ num=0; queen(0); scanf(“%d”, &n); for(i = 0; i < n; i++){ scanf(“%d”, &b); for(j = 0; j < 8; j++) printf(“%d”, ans[b - 1][j]); printf(“\n”); } }
实现中常见的问题
问题一: 使用枚举法,穷举8个皇后的所有可能位置组合,逐一判断是否可以互相被吃掉,得到超时错误;
问题二:对于多组输入,有多组输出,没有在每组输出后加换行符,得到格式错;
问题三:对输入输出的函数不熟悉,试图将数字转换成字符或者将8个整数转换成8位的十进制整数来完成输出,形成不必要的冗余代码。




