2022高考集训1
2022高考集训1
6月5日
前言:
说实话这高考不放假在学校待着就挺让人无语的,只能奥赛集训每天上午考试下午改题,当然我个人是非常喜欢考试的,我迷恋那种做题时的紧张,大脑飞速运转,灵光一现的想法,出分那一刻查看排名的刺激感,以及考好了嘲讽WintersRain的愉悦,我享受着这一切。可能有点病态了吧,不过确实如此
早上吃完饭去机房的路上碰见WintersRain,打赌,如果排名低中午就不回宿舍了,跪一中午键盘。然后临考前和他还特地向所有人说明了一下,可能他一直这种性子,要我说也不算张扬,就是没经历过社会的毒打hhhhhc。
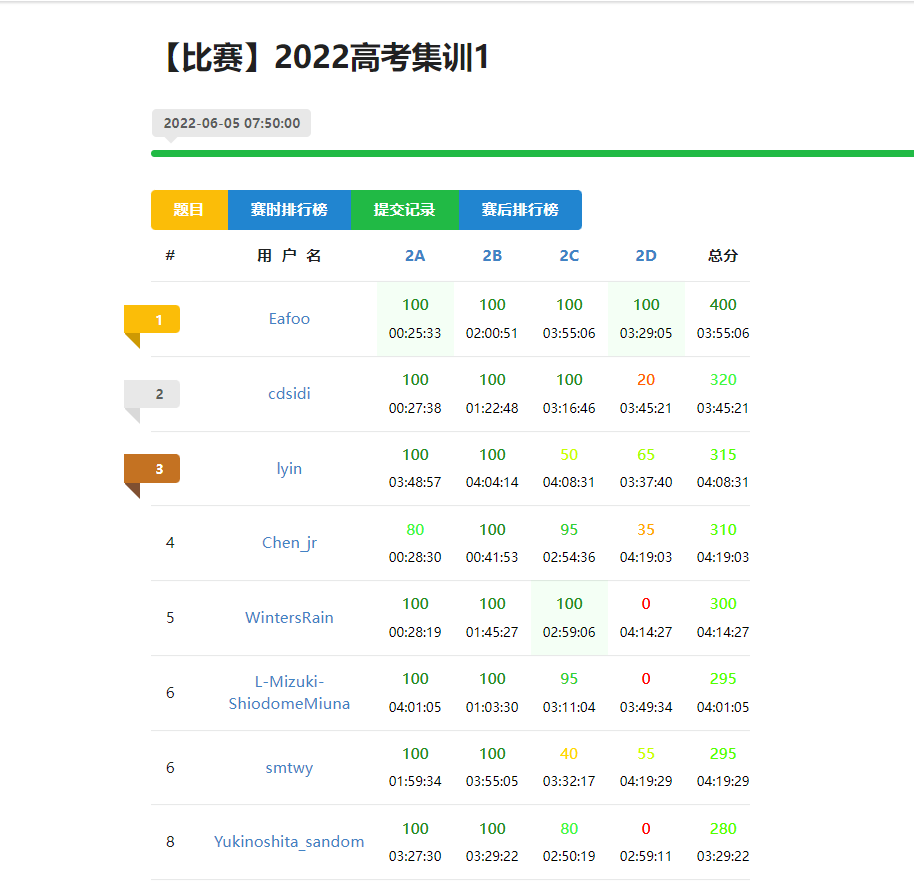
这次是44个人一起考,lyin,cd,eafoo都参加,多了五个人,所以我就比较激动,然后可能就加了点buff,贴下成绩,第六,说实话这个成绩还是不太满意,尤其是比WintersRain低五分。一考完他就来嘲讽说要让我跪键盘,然后我软磨硬泡装可怜说想吃饭就给糊弄过去了咳咳。
T1
2A


判断ip地址的合法性,他保证字符串中存在且仅存在四个分开的自然数,这一下就降低了一大堆难度,枚举一遍字符串,碰见数字就记录,碰见字符换成点,数字大了换255,注意一些零的问题,也就没有什么了。说白了就是个细节题,难度倒是没有什么,要说有哪些细节我现在忘了也懒得回想了,有兴趣可以看看我们hzoi其他人的博客,算是送分题,当然考细节致使有一半多的人这题都没有A,甚至不少分还很低。我倒是没啥感觉
查看代码
//2A
//三道字符串就有点恶心了
//它这个存在且仅存在真的一下把题目难度降低了不少
#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mx=40000;
char s[mx];
int a[mx];
int b[mx];
int cnt=0;
int ant=0;
int op=0;
void Solve(){
scanf("%s",s+1);
int flag;
int len=strlen(s+1);
s[len+1]='.';
for(int i=1;i<=len+1;++i){
if(s[i]>=48 && s[i]<=57){
a[++cnt]=s[i]-48;
// printf("a[]=%d\n",a[cnt]);
}
else {
if(s[i]!=46){
flag=1;
}
else op++;
// printf("cn=%d\n",cnt);
if(cnt==0)continue;
int at=0;
if(a[1]==0 && cnt==1){
b[++ant]=0;
b[++ant]=46;
cnt=0;
continue;
}
else if(a[1]==0)flag=1;
for(int j=1;j<=cnt;++j){
at=at*10+a[j];
if(at>255){
at=566;
break;
}
}
// printf("at=%d\n",at);
if(at>255){
flag=1;
b[++ant]=2;
b[++ant]=5;
b[++ant]=5;
}
else if(at==0){
b[++ant]=0;
}
else {
int kt=1;
for(int j=1;j<=cnt;++j){
if(a[j]!=0){
kt=j;
break;
}
}
for(int j=kt;j<=cnt;++j){
// if(j==1 && a[1]==0)continue;
b[++ant]=a[j];
// printf("ant=%d a[%d]=%d i=%d\n",ant,j,a[j],i);
}
}
cnt=0;
b[++ant]=46;
}
}
if(op>4)flag=1;
if(flag==1){
printf("NO\n");
for(int i=1;i<=ant-1;++i){
if(b[i]==46){
printf(".");
}
else {
printf("%d",b[i]);
}
}
printf("\n");
}
else {
printf("YES\n");
}
//肯定会有一些遗漏情况,想到再说
}
int main(){
freopen("ip.in","r",stdin);
freopen("ip.out","w",stdout);
Solve();
return 0;
}T2
2B


你会得到一个长度为n的字符串,这个字符串有且只有两个字符:A和P。我一看又是字符串心就有点凉,我因为牛棚回声到现在也不会写(这事其实也挺搞笑的,四年了)所以对字符串有种天然恐惧。然后去看T3,T4,最终又回来了。把题干读了读,认真看了四五分钟,在纸上写了写,DP->可n—>AP,PP, !woc思路题? 我的思路过程大概就是这样,这东西说结论我不太认为是,就是个小思路题,要说证明我也不会,我认为就挺显然的,AP和PP可消,那肯定是用P去尽量匹配前面的A把A消掉,最后剩下pp再互相消。不会出现什么A围着P的情况,因为P碰见A就消。所以一个思路题又挂了多少人啊
查看代码
//2B
#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mx=100000+1000;
//这种显然的思路题真的有考的必要嘛
//这还没t1难度大,莫名想到一个好玩的事,去写DP的好像真应了题名hhhhhhhhc
//在这里立个flag,下会一定要去学写对拍,一定!!!!!
char s[mx];
void Solve(){
scanf("%s",s+1);
int len=strlen(s+1);
int cnt=0;
int ant=0;
int ans=0;
for(int i=1;i<=len;++i){
if(s[i]=='A')cnt++;
else {
if(cnt!=0){
cnt--;
}
else {
ant++;
}
}
}
ant=ant%2;
ans=cnt+ant;
printf("%d\n",ans);
}
int main(){
freopen("apstr.in","r",stdin);
freopen("apstr.out","w",stdout);
Solve();
return 0;
}T3
2C



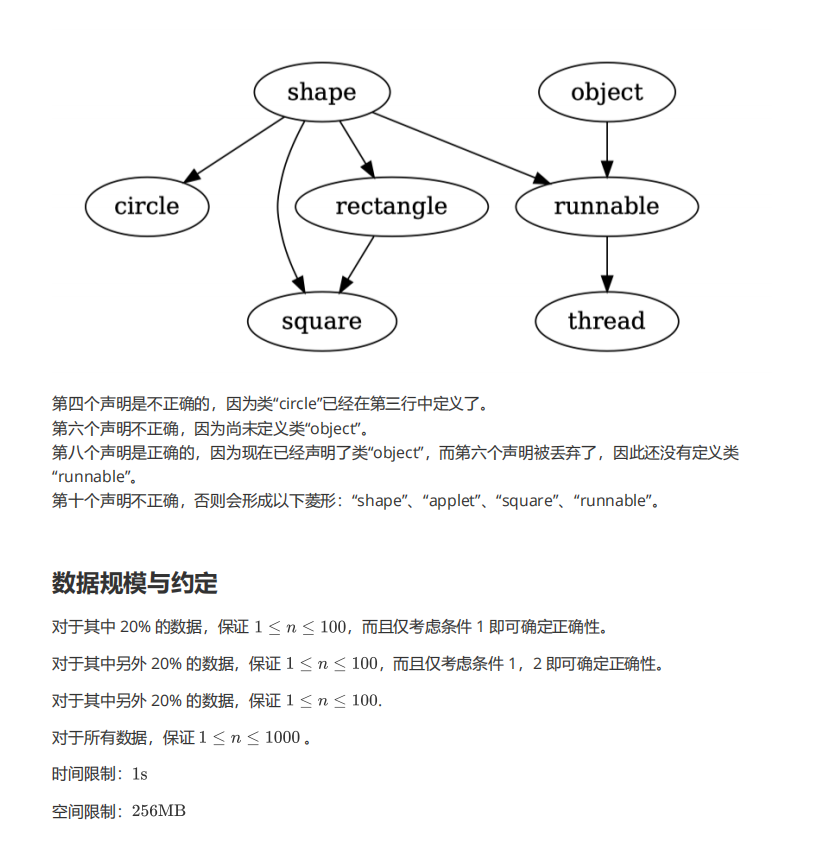
不允许在类层次结构中出现所谓的菱形。说实话这个题也很简单,举个洛谷难度的例子,(自己举得可能不太恰当),T4紫题肯定有,能不能近黑不好说,这题说是蓝题我觉都难。它就是考你会不会用STL。但是当时同样两道新定义题,我就是放弃了它去写T4,当然送的40分不要白不要,这几道题据他们说是教练买的,所以网上查不到题解,这不重要。关键是,只有图片,所以我们考试的时候样例输入只能自己一个个手打,恶心死我了。开个map,显然,直接查询是否出现过,以及直接赋值还是很方便。然后还要用一个触及我知识盲区的东西,好像叫bitsite?md我忘了。351238告诉我这东西好像就是记录0,1状态,这个菱形说白了,就是看两个单词往上有没有共同祖先,直接用它一比就行,特方便,当然我现在还没有改A,回头再补代码。
T4
2D
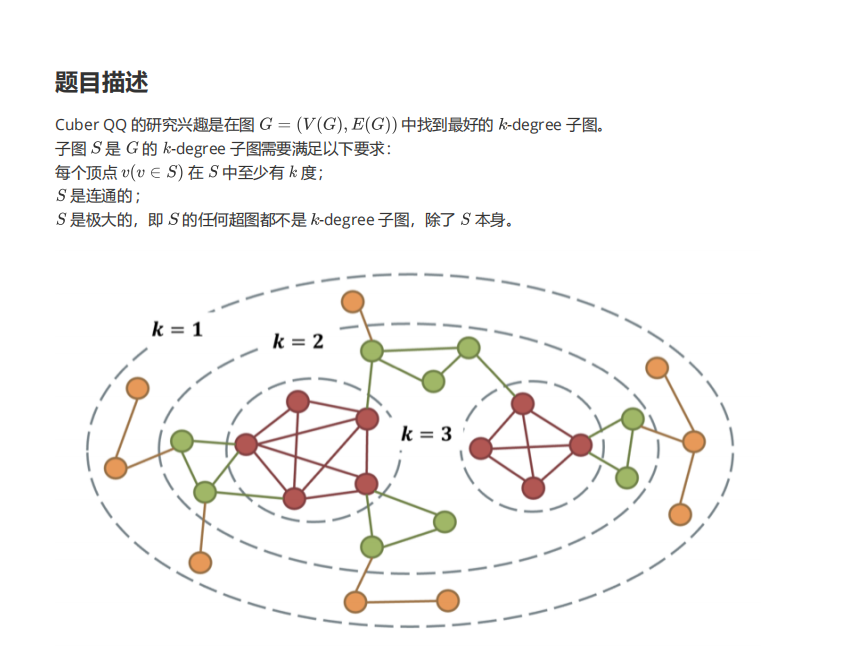

我就果断放弃T3,只写了个40暴力。 考试一共四个小时,分配了近三个小时给这个题,当然我考场确实写A了,最后因为一个细节问题>写成>=被卡了一半分。我觉得这固然是遗憾,但也是自己能力不行的体现,为什么eafoo就不会有这种问题,为什么他就能AK,所以大佬太强了%%%%%%%%。自己还是要反思
Cuber QQ的研究兴趣 连定义都说的稀里糊涂真的好嘛,k-degree子图,说实话这个题挺好的,不要去管超图是什么东西
题意理解:对于一个图,图中任意一个点的度值不小于k。同时只要给它加点,它的k值就会降低,那么我们就认为它是一个k-degree图,它是极大的。反之,如果给一个图加点它的k值不变或者升高,那么他就不是k-degree子图
观察给图,两堆红点都是3-degree子图,给红点加一个绿点,它的k值一定会被降低,所以它是。同时加上部分红点加上部分绿点不是k-degree子图,因为它再加更多的绿点k值不会降低,这里就解决了与Anastasia和351238讨论的定义问题,当然351238可能自己都没有意识到她提出了这个问题。回去洗澡了,明天再说
继续
催第四题的比较多,先简单写一下第四题的题解
这个题从下午两点到刚才8点40,一共整整讲了十遍,讲得我口干舌燥
后来lyin出了几组数据hack了本来就硕果仅存的通过的几个人(除了他自己全hack了),再后来我又改A
得到lyin亲口承认,只有hack你像hack O2一样,无法hack,他还说因为我们的诚挚的友谊,是挚友所以他无法hack,hhhhhhc笑死了
这里先说一下,因为这个题反正我们是没有找到题解,老师发的正解不说人话,我是没能看懂。所以几种思路方法都是我们几个自己琢磨出来的。下午讲题的时候虎没让eafoo大佬组织(hzoi惯例:考后讲题的时候赛时rk1是组织者,教练不会插手),让WintersRain讲的,前几题没有啥,就是他讲第三题的思路一步步推进时,讲到60分的方法,来了一句“仅凭这个显然是无法让wy跪键盘的,所以我们要继续思考”,然后当时所有人都看我,我当时只想消失。
第四题只有eafoo做出,他大概讲了讲,当然考试的时候这题基本没有什么人看,所以也就我问了问,其他大部分人当时还很陌生(这就是后来我又讲了10遍,基本给2机房所有人都讲了一遍的原因)。eafoo方法是O(n*n)的暴力 先把最大k-degree子图整个找出,然后依次把外围的点删去,每删一层算一个答案。 我是O(n*根号n) 先依据k值分层找出每层的点,然后以k值从大往小依次去合并,每并一层算一个答案。lyin的方法最厉害 O(n+m+n) 开一个桶,依据度数把点插进去,删点时删度,如果一个点度变小就把指针往回拨,因为最多往回拨m次,或者说移动m个距离,所以说是m+n+n。当然他这种方法没有人能听懂,我勉强理解他是什么意思,但我也写不出来。。。。。 后来lyin搞了两组数据,加了上去,把除了他自己全hack了,我加了个快读,把队列改成数组模拟,就又A了。当然还是O2太强了。lyin给我输出了一下,说循环确实是跑了1e9次,但是让O2给降下了。当然如果这个题数据再加强我就悬了,数据再加强就是纯黑题,估计除了lyin没有人能A
就图来看
显然,我们要找出 k=3 ; k=2,3; k=1,2,3一共三个解,去比较大小
先说怎么找出它们,我们用一个vector存储不同k-degree下的所有结点
例如ve[1]就存了所有的黄点,ve[2]就存了所有的绿点,ve[3]就存了所有的红点
这里用到拓扑排序的思想(当然我考试的时候根本没有去想到这个是拓扑排序,就自然而然的写出来了)
1.记录所有点的度(这个怎么记录都行)
2. 从度最小的开始遍历,且必须从最小的开始遍历 把所有度相同的点扔进一个ve,同时遍历这个点的所有儿子,它们的度都减1
如果一个点处在k值为1的环里,那么它一定连着一条度为1的点,如果这个点想要成为k=2的点,就需要那个度为1的点也是k=2的点,也就是说,度为1的点就等同于被删去了,它的存在不会为k值更大做任何贡献,它不足以支撑那个点在k=2的环里立足
如果有那个图对着讲会更好,我回头再做
3.循环完毕,我们就得出了想要的ve
怎么去寻找n,m,b的值
我们从k值最大开始,一层层往外扩展,且必须从最大开始,不能算k=1,2的一个解
因为 (k+1)-degree 一定属于k-degree ,k里的点都消失,k+1里的点的k值最小依旧是k+1,因为k里的点本身就不会对k+1的点在k+1里立足做任何贡献,它们的消失对k+1无影响
但如果k+1消失,k里的点的k值最小可能就不是k了,k+1里的点对于k里的点的k值绝对是做>=的贡献的
用并查集记录扩展关系,同时带权记录n,m,k
这就是整体的一个大思路,更为重要的是代码的具体实现以及为什么这么做,这些东西我就都放代码里了,很多东西还是很有价值的,建议细细琢磨一下
//2D
//求最大子图的tarjan的强连通思想
//魔法少女运用并查集维护相对关系的思想
//再有点带权并查集银河英雄传说的思想
#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mx=1000000+1000;
int n,m;
ll M,N,B;
int len;
int du[mx];//记录节点度数
int head[mx*5];
int fa[mx];
ll ans=-999999999999999999,an1;
int q[mx];
int l,r;
struct Nodee{
int belong;//这个点属于哪个k-degree图,belong存的是k值 它属于vector体系
int ns;//这个点所属联通块的点数
int bs;//边界边数
int ms;//边数
//因为我们用并查集维护关系,所以除了father的值,其它的值都只是中转,并不是严格定义上的 “这个点所属联通块的点数”
}o[mx];//下标是点的编号
struct Node{
int from;
int to;
int next;
}e[mx*5];//建图
vector <int> num[mx];//储存k-degree的vector
void Insert(int u,int v){
e[++len].from=u;
e[len].to=v;
e[len].next=head[u];
head[u]=len;
du[u]++;
} //前向星建图并记录度数
inline ll read(){
ll x=0;
ll w=1;
char ch=getchar();
while(isdigit(ch)==false){
if(ch=='-')w=-1;
ch=getchar();
}
while(isdigit(ch)==true){
x =(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*w;
}
int find(int rt){
if(fa[rt]==rt)return rt;
return fa[rt]=find(fa[rt]);
}
void merge(int x,int y){
int xx=find(x);
int yy=find(y);
if(xx!=yy){//如果本次相连的两个点不属于同一个祖先
fa[yy]=xx;
o[xx].ns+=o[yy].ns;//两个联通块的节点个数直接相加
o[xx].ms+=o[yy].ms+1;//边数相加并加1,加1是因为在并查集中,它们原本不相连,是我们此刻给它连了一条边
//而它们之所以可以相连,是因为它们在原始图中是相连的,这条边一直存在
o[xx].bs+=o[yy].bs-2;//在并查集的定义中,此刻相连的这条边,原本在不相连时是两个连通块的边界边,它一连不是边界边,所以要减2
}
else {//如果属于同一个祖先
o[xx].bs-=2;//那么两个点之间这条边,原本是双方各自的边界边,此刻成了相连边,所以减2
o[xx].ms++;//加的就是之间这条边 ,和上一行那个是同一条边
}
//并查集这里为什么这么加一定要理解,这样我们就把题干要求的n,m,b通过带权并查集求出
}
void Solve(){
n=read();m=read();
M=read();N=read();B=read();
//如果不写快读会被lyin卡掉,来自“挚友”的hack
l=1;
r=0;
for(int i=1;i<=m;++i){
int x,y;
x=read();
y=read();
Insert(x,y);
Insert(y,x);
}
for(int i=1;i<=n;++i){
fa[i]=i;
o[i].ns=1;//初始化每个点都是一个独立连通块
o[i].bs=du[i]; //刚开始,对于一个“独立”的点而言,它的度数就是边界边数(所有相连的边都是边界边)
//这里提醒一下,并查集记录的是联通块间的相对关系,vector存的是k-degree子图,e前向星是存储整张原始图,三者相互独立
}
int cnt=0;
int maa=0;
for(int i=0;i<n;++i){//循环枚举k-degree的k值
for(int j=1;j<=n;++j){
if(du[j]==i){
if(i==0){//这个零度点的地方我处理的不太好,应该还可以再妙
cnt++;
}
else {
q[++r]=j;//如果度值等于当前k值,扔进队列
}
}
}
if(i==0)continue;
while(l<=r){
int u=q[l];
l++;//这里如果用queue会被lyin卡掉
num[i].push_back(u);//把相同度数的点放进一个ve
o[u].belong=i;//同时记录属于关系,这样后面操作更方便一些
//这两步跟强连通的存储差不多
cnt++;
for(int k=head[u];k;k=e[k].next){
int v=e[k].to;
du[v]--;//v点有一个相连的点u在k=i的范围内,u已经在i被归属,不会再对v点在更大的k-degree做贡献
//所以直接减去
if(du[v]==i)q[++r]=v;//这里就是开队列的妙处,如果v减去之后度值也属于i了,就压进去,存起来
}
}
l=1,r=0;
if(cnt==n){//假设有七个点,度的可能性为0到6,但是可能度为2的有3个,度为3的有4个
//我们直接找全了7个点,就直接break就行,没有必要再循环下去
//当然据lyin说当数据大了之后它总会跑到很大,后面多几次空循环也无所谓,所以其实没有什么用
maa=i;//记录所有的点,度数最大为几
break;
}
}
for(int i=maa;i>0;--i){//从k值最大的k-degree图开始,从里往外扩展
int nu=num[i].size();
for(int j=0;j<nu;++j){//枚举这个k-degree图中的所有点
for(int k=head[num[i][j]];k;k=e[k].next){
int v=e[k].to;
if(i<o[v].belong){//如果当前i(k)值小于v的点k值
//说明当前是小的外层,可以与内层相连
//比如如果是红点k=3,那么这里一直不会执行,因为它的k是最大的,所以只会执行下面那个
//把红点相互连起来。如果是绿点k=2,看最左边那个绿点,它可以连一个黄点k=1,没有任何用,跳过
//它还可以连一个红点,k=3,那么就会执行这一步,扩展出去
//这是用绿点向里连接,等于是又倒了一下。其实直接用红点向外连也行,而且更好理解
//但是当时我考试就这么麻烦的写得
//结果他们改题就都这么写hhhhhhhc,这才是最为高深的防伪标记
merge(num[i][j],v);
continue;
}
if(i==o[v].belong && num[i][j]<v){//如果k值一样也要相连
//int u=num[i][j]. u<v,因为这是无向图,所以u,v可以互相找到,但是边只有一条
//如果你重复合并值肯定就错了,所以这就保证了只会连一次,写成v<u也行
//其实就相当于一个bool vis,但是这个题一个点可能会被连接多次,写vis不好处理
//而且这么写岂不是更帅,并起到一个强者检测器(这个词是给351238讲的时候想到的)的功能
//因为这实际上就是一个图论找边不用vis的小优化,真正强的一眼就能看透
//但是看不懂或者不愿意思考的肯定就很难了(这是351238说的,我没有别的意思hhhhhhc)
merge(num[i][j],v);
}
}
}
for(int j=0;j<nu;++j){
//这里最后把这个k-degree子图的所有点再都循环一遍,找father,求解
//一定要都循环一遍,因为实际数据可能会有多个联通块(它有的数据甚至有两万多个零度点)
//不同联通块可能都有k值为2的点,它们在并查集肯定无关联,但是在ve中都存到一起了
//就比如图的两块红区域,就要分开都算一遍,因为没有绿点加进来的时候它们肯定不连通
int fat=find(num[i][j]);
ll op=M*o[fat].ms-N*o[fat].ns+B*o[fat].bs;
if(ans<op){
ans=op;
an1=i;
}
}
}
printf("%d %lld\n",an1,ans);//ok,开始调试环节
}
int main(){
// freopen("data.in","r",stdin);
// freopen("out.out","w",stdout);
// freopen("kdgraph.in","r",stdin);
// freopen("kdgraph.out","w",stdout);
Solve();
return 0;
}我贴下lyin的桶,当然这位大佬属于装在套子里的人,我俩认识四年,初三还一个班,我也从来没见过他脱下那个外套(除了迫于我们老班的淫威,穿我们初三那高贵的清华紫班服),每天套个外套拉链往上一拉hhhhc(这是鑫大佬说的),所以他基本不会写题解。我挂一下他:lyin大佬
查看代码
#include <bits/stdc++.h>
#define fre(x) freopen( #x ".in", "r", stdin), freopen( #x ".out", "w", stdout )
using namespace std; typedef long long ll; typedef unsigned long long ull; typedef double db; typedef long double ldb;
const int N = 1e6 + 10;
mt19937 mt( (ull)(new char) );
int Rand ( int l, int r ) { return uniform_int_distribution<>(l,r)(mt); }
int n, m, kn, km, kb, du[N]; vector <int> vec[N];
struct BCJ
{
int fa[N], sm[N], sn[N], sd[N];
void Init ( int n ) { for( int i = 1; i <= n; ++i) fa[i] = i, sm[i] = 0, sn[i] = 1, sd[i] = du[i]; }
int Find ( int x ) { return x == fa[x] ? x : fa[x] = Find(fa[x]); }
void Merge ( int x, int y )
{
int fx = Find(x), fy = Find(y); if( fx == fy ) return; if( sn[fx] > sn[fy] ) swap( fx, fy );
fa[fx] = fy, sm[fy] += sm[fx], sn[fy] += sn[fx], sd[fy] += sd[fx];
}
ll Calc ( int x ) { return sn[x] == 1 ? -LLONG_MAX : 0LL + 1LL * km * sm[x] + 1LL * kn * sn[x] + 1LL * kb * ( sd[x]-2LL*sm[x] ); }
}S;
struct Graph
{
struct Edge { int to, next; } E[N<<1];
int ind, head[N];
void Insert ( int u, int v ) { ++ind, ++du[u], E[ind].to = v, E[ind].next = head[u], head[u] = ind; }
void Link ( int u, int v ) { Insert( u, v ), Insert( v, u ); }
vector <int> bin[N]; bool vis[N]; int top;
bool Select ( int k, int &u ) { while( bin[top].empty() && top <= k ) ++top; if( top > k ) return false; u = bin[top][ bin[top].size()-1 ], bin[top].pop_back(); return true; }
void Solve ()
{
for( int i = 1; i <= n; ++i) bin[ du[i] ].push_back( i ); top = 0;
for( int k = 1, u = 0; k <= n; ++k) while( Select( k, u ) )
{
if( vis[u] ) continue; vec[k].push_back(u), vis[u] = true, S.sm[u] = top;
for( int i = head[u]; i; i = E[i].next ) if( !vis[ E[i].to ] ) bin[ --du[ E[i].to ] ].push_back( E[i].to ), top = min( top, du[ E[i].to ] );
}
for( int i = 1; i <= n; ++i) vis[i] = 0;
ll maxi = -LLONG_MAX, maxk = 0;
for( int k = n; k >= 1; --k)
{
reverse( vec[k].begin(), vec[k].end() );
for( auto u : vec[k] ) { vis[u] = true; for( int i = head[u]; i; i = E[i].next ) if( vis[ E[i].to ] ) S.Merge( u, E[i].to ); }
for( auto u : vec[k] ) if( maxi < S.Calc( S.Find(u) ) ) maxi = S.Calc( S.Find(u) ), maxk = k;
}
cout << maxk << " " << maxi << "\n";
}
}G;
void Solve ()
{
cin >> n >> m >> km >> kn >> kb, kn = -kn;
for( int i = 1; i <= m; ++i) { int a, b; cin >> a >> b, G.Link( a, b ); }
S.Init(n), G.Solve();
}
signed main ()
{
fre(kdgraph);
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0); Solve(); return 0;
}后记:
后来晚上回去我就搂着WintersRain一副舔狗样(当然kiritokazuto的舔狗故事我们有时间再讲),生怕他拿跪键盘说事。但他还是提了,那我是什么人啊,我这个人脸皮厚的跟城墙一样,没脸没皮,内心强大,他问我什么时候跪,我说我晚上跪你床上行不行?然后他不敢说话了hhhhhhhc,还得是我。晚上回去又给myh打电话大概说了说,当然因为这通电话导致我没有洗澡 以至于早上起来用凉水洗澡然后去跑操搞得我第二天下午头疼感冒差点挂了就是后话了。此刻欢乐的我还不知道第二天要经历什么。。。。我得补一句我刚才看了一眼Kamisato_Ayaka的博客2022高考集训1他第一天挂了,然后说希望第二天不会挂,结果第二天20个人爆零,真就众生平等hhhhhhc


