初步网络最大流的算法及详解
网络最大流
众所周知,网络流是图论的一个很重要的内容,也很有难度(主要难在建模)。
网络流的基础概念这里提一下:
容量网络:设G(V,E),是一个有向网络,在V中指定了一个顶点,称为源点(记为Vs),以及另一个顶点,称为汇点(记为Vt);对于每一条弧<u,v>属于E,对应有一个权值c(u,v)>0,称为弧的容量.通常吧这样的有向网络G称为容量网络.
这里主要讲一下网络流最简单的一个分支:网络最大流。
什么是网络最大流?
通俗的说,如果把网络流比作水流,源点比作水龙头,汇点比作农田,边表示水管,那么,网络最大流表示的就是水龙头放水经过自来水管能够灌溉农田的最大水量。路途中其流量必然不能超过管的容积(否则管就爆了)。
下面给出一张图理解(字有点丑,不要介意):
s为源点,t为汇点,
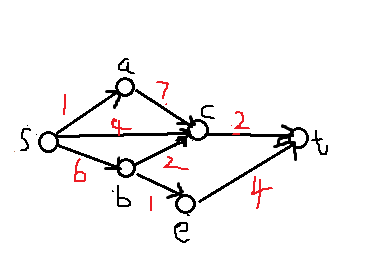
如图,有s->a->c->t,经过容量为1,7,2的边,路径最大流为1(路径中最小的边)。
s->c->t,经过容量为4, 2的边,但容量为2的边剩余容量为0,所以流为1,
s->b->c->t,经过容量为6,2,2的边,路径c->t中已经没有容量剩余,所以流为0,
s->b->e->t,经过容量为6,1,4的边,路径b->e中流最大为1,所以流为1.
所以,这张图的网络最大流为1+1+0+1 = 3.
怎么求网络最大流?
由定义,非常自然的,我们可以求出源点到汇点每条路径中水管容积最小的管的容积(水量不能超过每一条管的容积),累加这些路径的答案。
当图中不再存在增广路(即每一条路径中有一条边内没有容量剩余)时,就求出了网络最大流。
由此,我们推出了EK(Edmonds-Karp)算法。
EK算法
基于刚才的分析,我们可以通过BFS不断寻找增广路,直至图中不存在增广路为止。
在每轮寻找增广路的过程中,EK算法只考虑图中所有f(x, y) < c(x, y)的边,用BFS找到任意一条从S到T的路径,同时计算出路径上剩余容量的最小值minf, 则网络的流量可以增加minf。
具体实现步骤如下:
(1) BFS寻找增广路,若能找到,转步骤(2).否则转步骤(3)
(2) 更新剩余容量,将流累加.
(3) 输出累加的流,即为最大流。
代码如下:
1 #include<bits/stdc++.h>
2 #define ll long long
3
4 using namespace std;
5
6 const int inf = 1 << 29, N = 1000010;
7
8 int head[N], cnt = 1;
9 int n, m, s, t, maxflow = 0;
10 struct node{ int to, next,v;} e[N];
11
12 void add(int x, int y, int z){
13 e[++cnt].to = y; e[cnt].v = z;
14 e[cnt].next = head[x]; head[x] = cnt;
15 }
16 int v[N], incf[N], pre[N];
17 bool bfs(){
18 queue<int > q;
19 memset(v, 0, sizeof(v));
20 q.push(s); v[s] = 1;
21 incf[s] = inf; // 增广路上各边的最小剩余容量
22 while(q.size()){
23 int x = q.front(); q.pop();
24 for(int i = head[x];i;i = e[i].next){
25 if(e[i].v){
26 int y = e[i].to;
27 if(v[y]) continue;//如果点已经被标记过,则continue
28 incf[y] = min(incf[x], e[i].v);// 记录路径中剩余容量的的最小值
29 pre[y] = i;// 记录前驱,便于找到最长路的实际方案
30 q.push(y), v[y] = 1;
31 if(y == t) return 1;// 到达汇点结束BFS
32 }
33 }
34 }
35 return 0;
36 }
37 void update(){ // 更新增广路及其反向边的剩余容量
38 int x = t;
39 while(x != s){
40 int i = pre[x];
41 e[i].v -= incf[t];
42 e[i^1].v += incf[t];// 利用成对储存的xor 1技巧
43 x = e[i^1].to;
44 }
45 maxflow += incf[t];
46 }
47 int main(){
48 // freopen("input.in","r",stdin);
49 // freopen("output.out","w",stdout);
50 scanf("%d%d%d%d",&n, &m, &s, &t);
51 for(int i = 1;i <= m;i++){
52 int xx, yy, zz;
53 scanf("%d%d%d", &xx, &yy, &zz);
54 add(xx, yy, zz);
55 add(yy, xx, 0);
56 }
57 while(bfs()) update();
58 printf("%d\n", maxflow);
59 return 0;
60 }
时间复杂度为O(n*m*m),实际运用中远远达不到这个上界,效率较高,一般能够处理10^3 ~ 10^4 规模的网络。
对EK算法的优化——Dinic算法
我们发现,EK算法每轮可能会遍历整个残量网络,但只找出一条增广路,还有优化的空间。
我们不妨做一个优化,每次求完增广路后,构造分层图,删去已经标记的点,这样就避免了重复,节省了时间。
Dinic 算法核心思想:
首先BFS,在残量网络上构造分层图。
然后对每一个分层图分别dfs寻找增广路,实时更新剩余容量。
(1)初始化容量网络和网络流。
(2)构造残留网络和层次网络,若汇点不再层次网络中,则算法结束。
(3)在层次网络中用一次DFS过程进行增广,DFS执行完毕,该阶段的增广也执行完毕。
(4)转步骤(2)。
具体代码如下:
1 #include<bits/stdc++.h>
2 #define ll long long
3
4 using namespace std;
5
6 const int inf = 1<<29, N = 1000010;
7 int head[N], cnt = 0;
8 int n, m, s, t, maxflow;
9 struct node{ int to, next, v;} e[N];
10 queue <int> q;
11 void add(int x, int y, int z){
12 e[++cnt].to = y; e[cnt].v = z;
13 e[cnt].next = head[x]; head[x] = cnt;
14 }
15 int d[N];
16 bool bfs(){ // 在残量网络上构造分层图 ,求出每一个点的层次,用d[]表示。
17 memset(d, 0, sizeof(d));
18 while(q.size()) q.pop();// 清空队列
19 q.push(s); d[s] = 1;
20 while(q.size()){
21 int x = q.front(); q.pop();
22 for(int i = head[x];i;i = e[i].next){
23 int y = e[i].to;
24 if(e[i].v && !d[y]) { // 当前边还有剩余容量,且当前点未标记分层
25 q.push(y);
26 d[y] = d[x] + 1;//分层
27 if(y == t) return 1;// 到达汇点
28 }
29 }
30 }
31 return 0;
32 }
33
34 int dinic(int x, int flow){ // 在当前分层图上增广
35 if(x == t) return flow; // 若当前点为汇点则直接返回此时的流量
36 int rest = flow, k;
37 for(int i = head[x];i;i = e[i].next){
38 int y = e[i].to;
39 if(e[i].v && d[y] == d[x]+1){ // 当前边还有剩余容量,y 是 x 的后继顶点。
40 //更新x的后一层分层图
41 k = dinic(y, min(rest, e[i].v));//增广路中拥有最小流量的边,记为k.
42 if(!k) d[y] = 0; // 去掉增广完毕的点
43 e[i].v -= k; // 正向边减去k .
44 e[i^1].v += k; // 反向边增加k.
45 rest -= k; // 更新剩余容量
46 }
47 }
48 return flow - rest;
49 }
50 int main(){
51 // freopen("input.in","r",stdin);
52 // freopen("output.out","w",stdout);
53 scanf("%d%d%d%d", &n, &m, &s, &t);
54 cnt = 1;
55 for(int i = 1;i <= m;i++){
56 int xx, yy, zz;
57 scanf("%d%d%d", &xx, &yy, &zz);
58 add(xx, yy, zz);
59 add(yy, xx, 0); // 反向边初始为0.
60 }
61 int flow = 0;
62 while(bfs())// bfs 构造分层图,直到流到汇点后分层完毕。
63 while(flow = dinic(s, inf)) maxflow += flow; // 累加每一层的流
64 printf("%d\n", maxflow);
65 return 0;
66 }
Dinic算法时间复杂度为(n*n*m),实际上远远达不到这个上界,可以说是比较容易实现的的效率最高的网络流算法之一,一般能处理10^4~10^5的网络。
总结
这就是求网络最大流的两个主要算法(我不会其他算法QWQ)。
其实网络流除了网络最大流之外,还有最大流最小割,最小费用最大流,最大费用最大流等,以后再叙述。
