字典序算法

一个全排列可看做一个字符串，字符串可有前缀、后缀。

生成给定全排列的下一个排列.所谓一个的下一个就是这一个与下一个之间没有其他的。这就要求这一个与下一个有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。

[例]839647521是1--9的排列。1—9的排列最前面的是123456789，最后面的987654321，从右向左扫描若都是增的，就到了987654321，也就没有下一个了。否则找出第一次出现下降的位置。

就是找变化最小的。

例子：

【例】 如何得到346987521的下一个
    1，从尾部往前找第一个P(i-1) < P(i)的位置
            3 4 6 <- 9 <- 8 <- 7 <- 5 <- 2 <- 1
        最终找到6是第一个变小的数字，记录下6的位置i-1
    2，从i位置往后找到最后一个大于6的数
            3 4 6 -> 9 -> 8 -> 7 5 2 1
        最终找到7的位置，记录位置为m
    3，交换位置i-1和m的值
            3 4 7 9 8 6 5 2 1
    4，倒序i位置后的所有数据
            3 4 7 1 2 5 6 8 9
    则347125689为346987521的下一个排列

代码如下：

private static void PermutationList()
        {
            int fromIndex, endIndex, changeIndex;
            Sort(0, length - 1);
            do
            {
                // 输出一种全排列
                Output();
                fromIndex = endIndex = length - 1;
                // 向前查找第一个变小的元素
                while (fromIndex > 0 && words[fromIndex] < words[fromIndex - 1]) --fromIndex;//有重复字符的情况改为words[fromIndex] <= words[fromIndex - 1]
                changeIndex = fromIndex;
                if (fromIndex == 0) break;
                // 向后查找最后一个大于words[fromIndex-1]的元素
                while (changeIndex + 1 < length && words[changeIndex + 1] > words[fromIndex - 1]) ++changeIndex;
                Swap(fromIndex - 1, changeIndex);   // 交换两个值
                InvertArray(fromIndex, endIndex);   // 对后面的所有值进行反向处理
            } while (true);
        }

 

递归算法：

 

固定第一个字符，然后依次将后面的字符串与前面的交换，那么排列的个数就是除了第一个字符以外，其他字符的排列个数+1。也就是固定一个字符串之后，之后再将问题变小，只需求出后面子串的排列个数就可以得出结果。

 

 

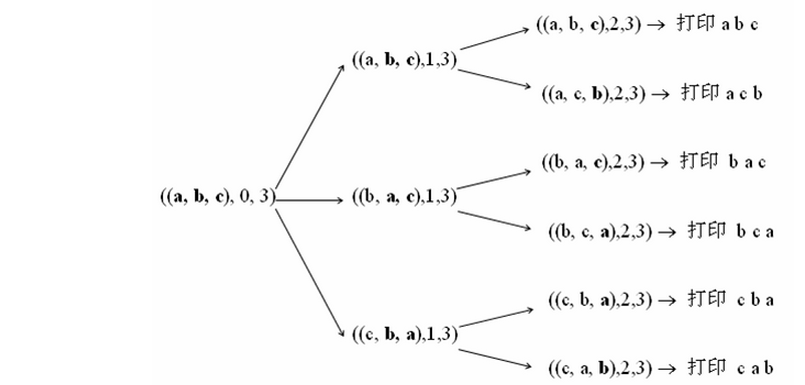
递归的出口，就是只剩一个字符的时候，递归的循环过程，就是从每个子串的第二个字符开始依次与第一个字符交换，然后继续处理子串。

代码如下：

public static void main (String[] args){
        Solution p = new Solution();
        System.out.println(p.Permutation("abc").toString());
    }
    public ArrayList<String> Permutation(String str) {
        List <String> res = new ArrayList();
        if (str != null&& str.length() > 0 ){
            per(str.toCharArray(),0,res);
            Collections.sort(res);
        }
        return (ArrayList)res;
    }
    public void per(char[] ch, int i,List<String> res){
        if ( i == ch.length-1){
            String val =String.valueOf(ch);
            if (!res.contains(val))//判断是否重复，重复则不加入
                res.add(val);
        }
        else{for (int j = i ;j<ch.length;j++){
        swap(ch,i,j);
        per(ch,i+1,res);
        swap(ch,i,j);
    }}}
 
     public void swap(char[] cs, int i, int j) {
        char temp = cs[i];
        cs[i] = cs[j];
        cs[j] = temp;
    }

 

参考自：https://www.cnblogs.com/cxjchen/p/3932949.html

　　　　https://www.cnblogs.com/pmars/archive/2013/12/04/3458289.html