一道算法题-求三个矩形的交集矩形。
给定矩形的定义如下:
struct Rect{ int x; //表示矩形的左上水平坐标 int y; //表示矩形的左上垂直坐标 int w; //表示矩形宽度 int h; //表示矩形高度 };
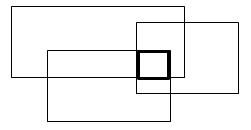
现在给三个矩形,求三个矩形的交集,如果没有交集,那么矩形的x,y,w和h均赋值为-1。例如下面示例图,求出三个矩形相交的粗线线框表示的矩形。
解题思路:
解题思路很重要,没有集体思路,题目肯定是做出不来的。下面给出本人的解题思路:
(1)判断三个矩形有没有交集。这个是难点,该怎么做呢?可以在x轴方向将三个矩形按x的大小从左到右排列,判断两两矩形在x轴方向是否有交集,如果有任意一对没有相交那么三个矩形没有交集。判断方法是如果rectB.x>=rectA.x+rectA.w的话,那么说明rectA和rectB之间没有交集。
同理,在y轴方向做同样的判断;
(2)求出任意两个矩形的交集矩形,再将交集矩形与第三个矩形再求交集,可得最后的交集矩形。
有了正确和清晰的思路,就可以写代码了,下面给出本人的实现,可供网友参考。
1 #include <iostream> 2 using namespace std; 3 #include <vector> 4 #include <algorithm> 5 6 struct Rect{ 7 int x; //表示矩形的左上水平坐标 8 int y; //表示矩形的左上垂直坐标 9 int w; //表示矩形宽度 10 int h; //表示矩形高度 11 }; 12 13 //按照x递增排序 14 bool compareX(const Rect& rectA,const Rect& rectB ){ 15 return rectA.x<rectB.x; 16 } 17 18 //按照y递增排序 19 bool compareY(const Rect& rectA,const Rect& rectB ){ 20 return rectA.y<rectB.y; 21 } 22 23 //判断三个矩形是否相交 24 bool isIntersect(const Rect& rectA,const Rect& rectB,const Rect& rectC){ 25 Rect rectLeft,rectXMid,rectRight; //从左向右的矩形 26 Rect rectTop,rectYMid,rectBelow; //从上到下的矩形 27 28 //将矩形按照x由左向右排序 29 vector<const Rect> vec; 30 vec.push_back(rectA); 31 vec.push_back(rectB); 32 vec.push_back(rectC); 33 sort(vec.begin(),vec.end(),compareX); 34 rectLeft=vec[0],rectXMid=vec[1],rectRight=vec[2]; 35 36 //水平方向任意两个矩形没有交集 37 if(rectXMid.x>=rectLeft.x+rectLeft.w||rectRight.x>=rectXMid.x+rectXMid.w||rectRight.x>=rectLeft.x+rectLeft.w) 38 return false; 39 40 //同理将矩形按照y由上往下排序 41 sort(vec.begin(),vec.end(),compareY); 42 rectTop=vec[0],rectYMid=vec[1],rectBelow=vec[2]; 43 44 //垂直方向任意两个矩形没有交集 45 if(rectYMid.y>=rectTop.y+rectTop.h||rectBelow.y>=rectYMid.y+rectYMid.h||rectBelow.y>=rectTop.y+rectTop.h) 46 return false; 47 return true; //三个矩形有交集 48 } 49 50 //两个矩形的交集,前提是两个矩形一定有交集 51 Rect intersection(const Rect& rectA,const Rect& rectB){ 52 Rect resRect; 53 resRect.x=rectA.x>rectB.x?rectA.x:rectB.x; //选最右边的矩形的x作为交集的x 54 resRect.y=rectA.y>rectB.y?rectA.y:rectB.y; //选最下面的矩形的y作为交集的y 55 //选择左边矩形(x坐标较小者)的右边的作为交集矩形的右边,这样就可以求出交集矩形的宽度 56 resRect.w=rectA.x+rectA.w<rectB.x+rectB.w?rectA.x+rectA.w-resRect.x:rectB.x+rectB.w-resRect.x; 57 //同理,选择上面矩形(y坐标较小者)的下边的作为交集矩形的下边,这样就可以求出交集矩形的高度 58 resRect.h=rectA.y+rectA.h<rectB.y+rectB.y?rectA.y+rectA.h-resRect.y:rectB.y+rectB.h-resRect.y; 59 return resRect; 60 } 61 62 63 //求三个矩形的交集 64 Rect threeIntersection(const Rect& rectA,const Rect& rectB,const Rect& rectC){ 65 Rect res; 66 bool isIntersectBool=isIntersect(rectA,rectB,rectC); 67 if(isIntersectBool){ //有相交 68 Rect rectAB=intersection(rectA,rectB); 69 res=intersection(rectAB,rectC); 70 } 71 else 72 res.x=res.y=res.w=res.h=-1; 73 return res; 74 }
测试结果如下:
int main(){ Rect rectA,rectB,rectC; //测试案例1 //rectA.x=0,rectA.y=0,rectA.w=1,rectA.h=1; //rectB.x=1,rectB.y=1,rectB.w=1,rectB.h=1; //rectC.x=2,rectC.y=2,rectC.w=1,rectC.h=1; //测试案例2 rectA.x=0,rectA.y=0,rectA.w=2,rectA.h=2; rectB.x=1,rectB.y=1,rectB.w=1,rectB.h=1; rectC.x=1,rectC.y=1,rectC.w=1,rectC.h=1; Rect resRect=threeIntersection(rectA,rectB,rectC); if(resRect.x!=-1){ //有相交 cout<<"resRect.x:"<<resRect.x<<endl; cout<<"resRect.y:"<<resRect.x<<endl; cout<<"resRect.w:"<<resRect.x<<endl; cout<<"resRect.h:"<<resRect.x<<endl; } else cout<<"not intersect"<<endl; getchar(); }
测试案例1输出:not intersect;
测试案例2输出:
resRect.x:1
resRect.y:1
resRect.w:1
resRect.h:1




