激活函数
神经网络做的主要事情就是分类,在上课中,最简单的问题为二分类问题,利用单层感知机,可以画出一条线将平面隔开分类。同样如果增加感知机个数,可以得到更强的分类能力,但是无论如何都是一个线性方程。只不过是线性的复杂组合,当然曲线可以用无限的直线去逼近,但是这显然会带来巨大的计算量。因此加入了激活函数,这样原本的线性方程表成了一个非线性方程。如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下每一层输出都是上层输入的线性函数,所以无论神经网络有多少层,输出都是输入的线性组合,与没有激活层效果相当,这种情况就是最原始的感知机了。正因为上面的原因,所以需要引入非线性函数作为激励函数。这样深层神经网络就有意义了。
relu,sigmoid和tanh激活函数
只是在本数据集和特定网络下的结果,网络结构:
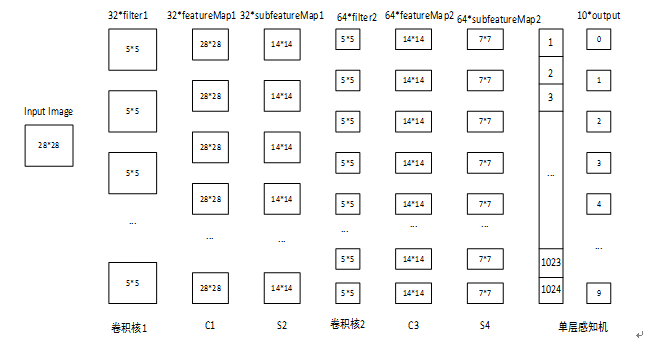
利用MNIST数据集,做了relu,sigmoid和tanh的实验,每次输入50个数据,迭代10000次,三种激活函数的正确率如图:

正确率relu>tanh>sigmoid。
收敛速度有很大的不同,在训练过程中,每迭代100次,会把加载的50个数据作为测试集,利用前一个模型计算一次正确率输出。迭代前2000次,不同激活函数正确率曲线如下:
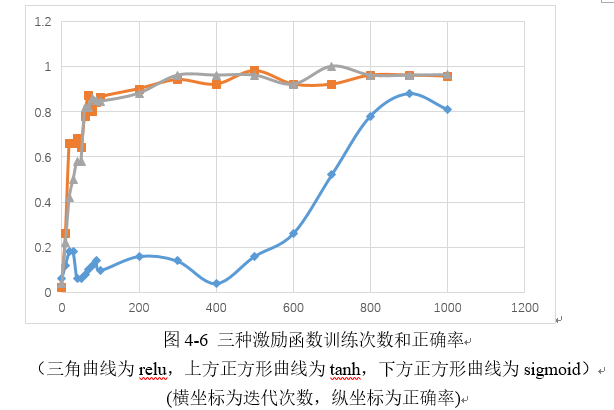
可见,sigmoid的收敛速度远远慢于tanh和relu激活函数,tanh和relu在100迭代左右已经开始收敛,而sigmoid在800次左右才可收敛。
原因分析: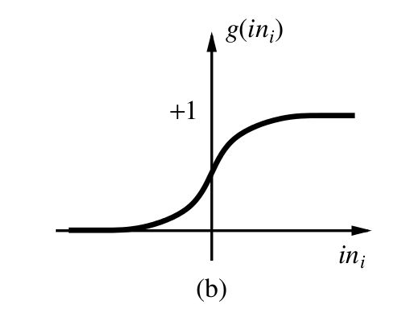
sigmoid函数,
sigmoid函数在在两段接近饱和区是,变换的很缓慢,导数趋近于0,在反向传播时,容易出现梯度消失的现象,造成信息的丢失。同时因为sigmoid函数是指数运算,计算量较大,导致反向传播求误差梯度是,计算量相对于relu会大很多,而采用relu激活函数,计算量会小很多。同样还有一个好处,relu函数会使得一部分神经元的输出为0,这样会使网络稀疏,减少了参数的依赖关系,缓解了过拟合的发生。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号