retrival and clustering : week 3 k-means 笔记
华盛顿大学 machine learning 笔记。
K-means algorithm
算法步骤:
0. 初始化几个聚类中心 (cluster centers)μ1,μ2, … , μk

1. 将所有数据点分配给最近的聚类中心;
![]()
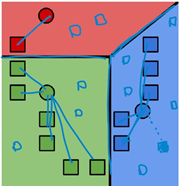
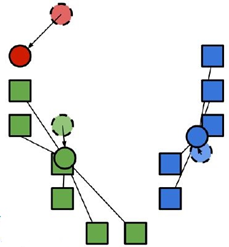
2. 将每个聚类中心的值改成分配到该点所有数据点的均值;
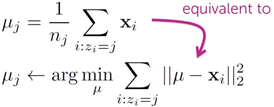
3. 重复1-2步骤,直到收敛到局部最优(local optimium).
#输入: #数据集 data #集群数 k #初始集群中心组 initial_centroids #最多循环次数 maxiter #输出: #集群中心组 centroids #数据点分配情况 cluster_assignment def kmeans(data, k, initial_centroids, maxiter): centroids = initial_centroids[:] prev_cluster_assignment = None for itr in xrange(maxiter): # 计算各数据点到各个centroid的距离 distances_from_centroids = pairwise_distances(data, centroids, metric='euclidean') # 将数据点分配到各个centroid cluster_assignment = np.argmin(distances_from_centroids, axis = 1) # 将每个centroid的值改成分配到该点的所有数据点的均值 new_centroids = [] for i in xrange(k): member_data_points = data[cluster_assignment == i] centroid = member_data_points.mean(axis = 0) # 格式转换 centroid = centroid.A1 new_centroids.append(centroid) new_centroids = np.array(new_centroids) centroids = new_centroids # 判断是否收敛到局部最优 if prev_cluster_assignment is not None and \ (prev_cluster_assignment==cluster_assignment).all(): break prev_cluster_assignment = cluster_assignment[:] return centroids, cluster_assignment
问题1: 算法结果为局部最优,受初始化选择的聚类中心影响很大,如何初始化?
k-means ++:
1.第一个聚类中心从随机点中随机选择。
2.对于每个数据点,计算到最近集群中心的距离。
3.从数据点中选择新的集群中心,数据点选择概率与它离最近的集群中心的距离成比例(使centroids之间离得越远越好)。
4.重复步骤2和3,直到k个中心全被选中。
特点:
随机初始化计算成本相对较高,但随后通常会更迅速地收敛,局部最优质量更高,运行时间短。
def smart_initialize(data, k): # k-means++ 方法 得到初始的centroids组 centroids = np.zeros((k, data.shape[1])) # 随机选择第一个centroid idx = np.random.randint(data.shape[0]) centroids[0] = data[idx,:].toarray() # 计算其他数据点到第一个centroid的距离 squared_distances = pairwise_distances(data, centroids[0:1], metric='euclidean').flatten()**2 # 选择接下来的 k-1 个centroids # 每个数据点被选中的概率与它离最近的centroid的距离成比例(即使得centroids之间离得越远越好) for i in xrange(1, k): idx = np.random.choice(data.shape[0], 1, p=squared_distances/sum(squared_distances)) centroids[i] = data[idx,:].toarray() # 更新每个数据点离已选择的centroids的距离 squared_distances = np.min(pairwise_distances(data, centroids[0:i+1], metric='euclidean')**2,axis=1) return centroids
问题2:如何评价聚类算法结果的质量?
两种聚类方法,第二种更符合我们对聚类算法的预期,如何评估聚类的结果?
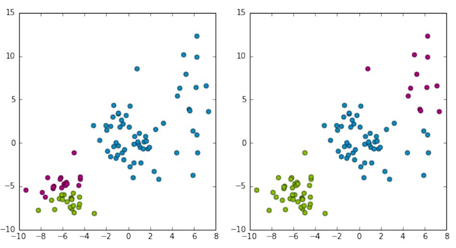
最小化距离的平方和:
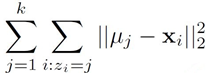
问题3: 如何选择合适的k?
随着k的增加,聚类算法的异质性(heterogeneity)会降低。
heterogeneity 表达式:

方法一:拐点法
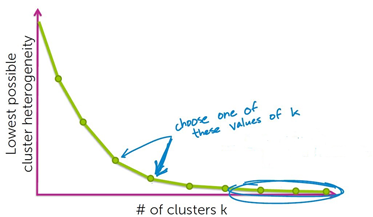
选取拐点处的k值。
方法二:均方根: ![]() (n个数据点)
(n个数据点)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号