图象恢复学习笔记(一)
Restoration: From Sparse and Low-rank Priors to Deep Priors 阅读笔记
来源:http://www.comp.polyu.edu.hk/~cslzhang
图象恢复问题描述
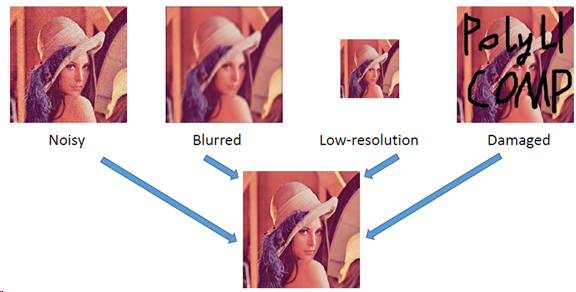
公式表示
𝒚 = 𝑯𝒙 + 𝒗 ,其中𝑯 是退化矩阵,𝒗 是加性噪声
图像恢复问题可以描述为给定观察到的y图像,从中恢复出原图像x。
图象恢复是一种不适定问题。
(适定问题是指定解满足下面三个要求的问题:① 解是存在的;② 解是唯一的;③ 解连续依赖于定解条件,即解是稳定的。这三个要求中,只要有一个不满足,则称之为不适定问题。)
图象恢复模型
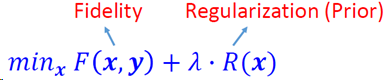
核心问题:
退化过程模型建立
合适的先验条件(good priors)
稀疏表示
回顾线性代数𝑨𝜶=𝒃, 如何求解𝜶?
A满秩方阵,𝜶=𝑨-1𝒃.
A列满秩矩阵(over-determined),有最小二乘解 𝜶= 𝑨†𝒃 (伪逆)
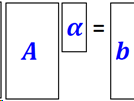
A行满秩矩阵(under determined)?
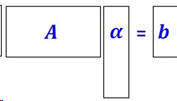
优化模型: 𝑚𝑖𝑛𝜶𝐽(𝜶) 𝑠.𝑡.𝑨𝜶=𝒃
不同目标函数𝐽(𝜶)可以得到不同的解,其中目标函数取

L2范数最小化的解为稠密解(解里有许多非0的值),但更多的时候,我们希望得到一个稀疏的解,即解里有许多0或接近0的值。
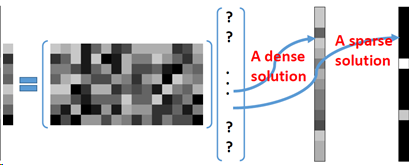
稀疏编码模型
为了得到稀疏解,取目标函数为L0范数。
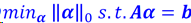
但L0范数最小化为非凸的NP-hard问题。
而L1范数最小化是L0范数最小化的最紧的凸松弛。
最为广泛使用的稀疏编码模型形式如下:
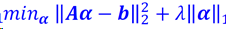
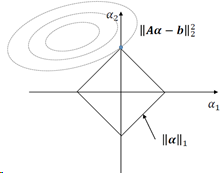
稀疏编码的算法
L0范数最小化-贪婪搜索
匹配追踪MP
正交匹配追踪OMP
L1范数最小化-凸优化
迭代再加权最小二乘
近似梯度下降(迭代软阈值ISTA)
增广拉格朗日方法(乘子交替方向法ADMM)
MP&OMP
匹配追踪(MP)和正交匹配追踪(OMP)要解决的问题可以具体表示为:
在过完备字典𝑨中选出k列,用这k列的线性组合近似表达待稀疏分解信号𝒃,表示为,𝒃=𝑨𝜶,求𝜶。
其中字典A和观测到的信号𝒃已知。
过完备字典,即原子个数远大于信号长度,𝒃=𝑨𝜶中,过完备字典𝑨为n*m尺寸,信号b长度为n*1,𝜶为m*1。
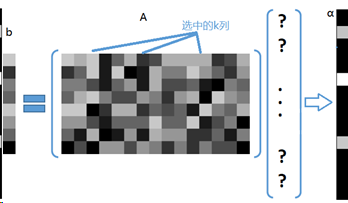
MP算法的基本思想:
从过完备字典矩阵A(也称为原子库中),选择一个与信号𝒃 最匹配的原子(某一列),最小二乘解逼近,再从信号𝒃中减去这部分,求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号𝒃可以由这些原子的线性和,加上最后的残差值来表示。
由于字典原子不是相互正交的,有可能会使得每次迭代的结果不是最优的,需要很多次迭代才能收敛。
OMP算法思想:
在正交匹配追踪OMP中,残差是总与已经选择过的原子正交的。这意味着一个原子不会被选择两次,结果会在有限的几步收敛。
具体步骤其实就是用施密特正交化使每次选择的原子(字典某一列,基)与已经选择过的所有原子正交。另外,求残差也不是直接减,而是减去在已经选择过的所有原子组成的空间上的正交投影。
增广拉格朗日方法
https://blog.csdn.net/itnerd/article/details/86012869
基于稀疏表示的图像恢复
用字典 D加强x的稀疏表示:

考虑到图象恢复模型:
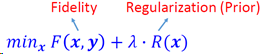
基于稀疏表示的模型为
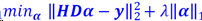
整个算法的流程为:
- 将图片y切割成重叠的图片块。
- 对于每个图片块,求解非线性L1范数稀疏编码问题:

(这个算法里,稀疏字典D是已知的)
- 重建每个图像块:
- 将重建的图像块重叠部分平均,重建图片x.
- 迭代以上步骤。
为什么要稀疏?
神经科学视角
Olshausenand Field’s Sparse Codes, 1996
目标:实现一种生成自然图像的编码策略,要求能同时保持位置、方向和带通特性。
解决方案:最大化稀疏性的编码策略:
E = -[preserve information] –lambda [sparseness]
•Bruno A. Olshausen, “Emergence of simple-cell receptive field properties by learning a sparse code for natural images.” Nature, 381.6583 (1996): 607-609.
•Bruno A. Olshausenand David J. Field. “Sparse coding with an overcompletebasis set: A strategy employed by VI?.” Vision Research, 37.23 (1997): 3311-3326.
贝叶斯视角
贝叶斯定理下的信号恢复
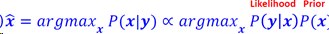
代入 𝒙 = 𝑫𝜶,假设𝜶符合指数分布:
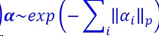
最大后验概率的解为
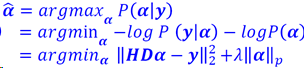
信号处理视角
如果一个信号可以用K个基线性表示,这个信号被称为K稀疏信号,如果K<<N,这个信号被称为可压缩的。
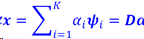
𝒚=𝑯𝒙=𝑯𝑫𝜶=𝑨𝜶
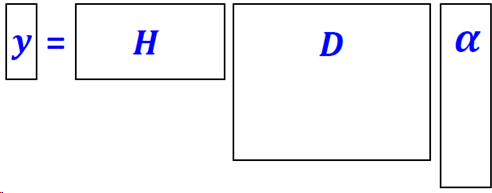
信号重建
如果信号是k稀疏的,则可以通过远小于信号矩阵尺寸(M<<N)的测量从y中恢复这个信号。

其中,测量矩阵A需要满足RIP条件。
RIP, 有限等距性质(Restricted Isometry Property, RIP)

王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报,2013,41(10):2041-2050.
字典学习
字典分类
分析字典
DCT、小波变换、Curvelets、Ridgelets, bandlets, …
学习字典
K-SVD、坐标下降 、多尺度字典学习、自适应PCA字典...
为什么要字典学习?
基于学习的过完备字典的稀疏模型比基于分析字典(如DCT字典、小波字典)效果更好。
为什么学过的词典更有效?
•更适合特定任务/数据。
•对字典的基dictionary atom)的数学性质没有严格限制。
•对模型数据更灵活。
•容易产生稀疏解。
字典学习算法
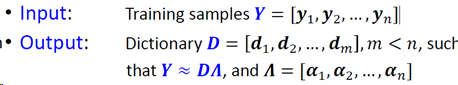
K-SVD (L0范数)
•Coordinate descent (L1范数)
•其他:多尺度字典学习、自适应PCA…
K-SVD
K-means是一种稀疏字典学习的特殊情况(即只用一个原子来近似整个样本,例如cluster中心),这种有选择性地对cluster标签和中心进行更新的思想可以在字典学习中采用。

K-SVD则是用一个K原子的字典D来近似样本。K-SVD的目标是要构造一个过完备字典D(k原子),然后选择最稀疏的系数解𝜶使得过完备字典D可以对其训练集相似的目标向量进行稀疏表示。
采用L0范数,每次更新D,只关注𝜶中非零值的个数。
M. Aharon, M. Elad, A. Bruckstein, K-SVD: An algorithm for designing over complete dictionaries for sparse representation, IEEE Transactions on Signal Processing, 54 (11), 4311-4322.
算法流程:
构造字典的算法分为两步:稀疏表示和字典更新。
首先要有一个初始化的字典D,用当前字典D对信号y进行稀疏表示,稀疏表示使用传统稀疏编码算法,例如MP、OMP。
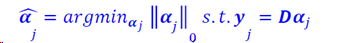
逐列更新字典向量:
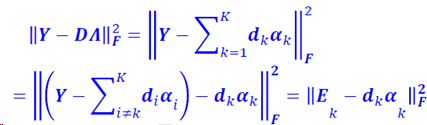
去掉字典第k列,得到误差矩阵Ek,对E做SVD分解E=UΛVT,U和V为酉矩阵,Λ是对角矩阵,对角元素从大到小排列,取U第一列表示dk,Λ最大元素和V第一个列乘积表示𝜶k,这样完成了字典D中一列的更新。
注意,只选择𝜶k中的非零元素,对相应的dk进行更新。即用𝜶k中非零元素构建一个新的矩阵Ωk,上式变为:
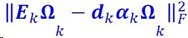
此时取EkΩk进行SVD分解。
参考:https://www.cnblogs.com/salan668/p/3555871.html
L1范数字典学习
L1范数字典学习采用与K-SVD相似的策略,L0范数方法(K-SVD)只关心非零值的数量,而对于L1范数方法,也要考虑参数的值。
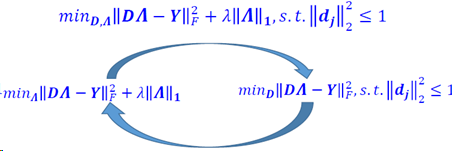
Meng Yang, et. al. "MetafaceLearning for Sparse Representation based Face Recognition," In ICIP 2010. (Code:http://www4.comp.polyu.edu.hk/~cslzhang/code/ICIP10/Metaface_ICIP.rar)
其他字典学习方法
多尺度字典学习
随着信号尺寸的增加,稀疏编码的复杂度呈指数上升。因此,大多数方法只适用于处理小图片块。为了能在大图片块上实现稀疏编码,多尺度方法可以提供一种在大尺度上对简单结构进行自适应建模、在小尺度上对细节进行自适应建模的方法。
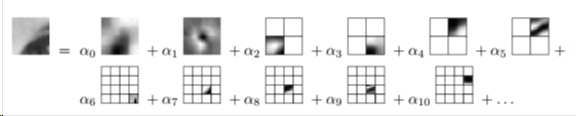
J. Mairal, et al., Learning multiscale sparse representations for image and video restoration.MultiscaleModeling & Simulation.
双重稀疏度:高维数据稀疏字典
为了建模高维数据,采用稀疏的稀疏字典。稀疏字典表示为𝑫=𝜱𝒁, 其中 𝜱是预定义的字典的基,例如DCT或小波。目标函数为
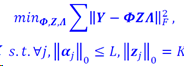
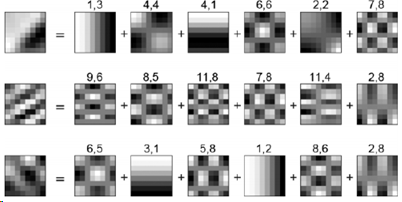
R. Rubinstein, et. al. Double Sparsity: Learning Sparse Dictionaries for Sparse Signal Approximation. IEEE Trans. on Signal Processing, 2010.
半耦合字典学习
用于复杂图像的建模
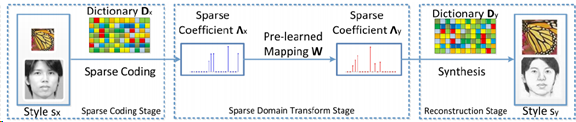
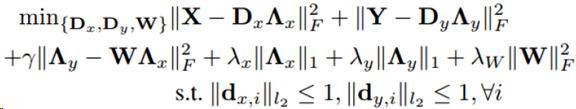
S. Wang, L. Zhang, Y. Liang, Q. Pan, "Semi-Coupled Dictionary Learning with Applications to Image Super-Resolution and Photo-Sketch Image Synthesis," InCVPR 2012.
•http://www4.comp.polyu.edu.hk/~cslzhang/SCDL/SCDL_Code.zip
自适应PCA字典选择
稀疏编码耗时较多,尤其是大字典。但为了对复杂图像的局部结构进行建模,通常需要一个很大的过完备字典。一个解决方法是学习一系列PCA字典,然后从中挑选一个来表示给定的图片块。
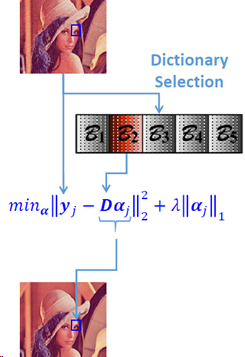
W. Dong, L. Zhang, G. Shi, X. Wu, Image deblurringand super-resolution by adaptive sparse domain selection and adaptive regularization, TIP 2011.
•http://www4.comp.polyu.edu.hk/~cslzhang/ASDS_data/TIP_ASDS_IR.zip
非局部中心化稀疏表示(NCSR)
局部自相似性
自然图像常常存在非局部自相似性,即对于一个指定的图像块,在图像中往往存在许多离得较远的图像块与其相似。

Buades, et al., A non-local algorithm for image denoising. CVPR 2005.
非局部中心化稀疏表示(NCSR)是一种简洁但非常有效的稀疏表示模型,它自然地集成了非局部自相似(NSS)先验和稀疏编码。
W. Dong, L. Zhang and G. Shi, “Centralized Sparse Representation for Image Restoration”, in ICCV 2011.
W. Dong, L. Zhang, G. Shi and X. Li, “NonlocallyCentralized Sparse Representation for Image Restoration”, IEEE Trans. on Image Processing, vol. 22, no. 4, pp. 1620-1630, April 2013.
http://www4.comp.polyu.edu.hk/~cslzhang/code/NCSR.rar
NCSR主要思想
对于真实信号x:
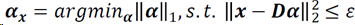
对于观测信号y:
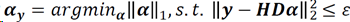
SCN(Sparce coding noise)稀疏编码噪声:
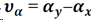
为了更好地重建x,必须降低稀疏编码噪声:
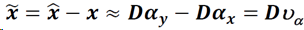
NCSR目标函数
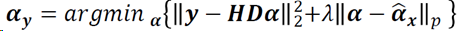
其中 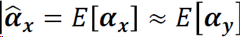
核心思想即抑制稀疏编码噪声。
NCSR的解
[𝜶𝒚]非局部估计
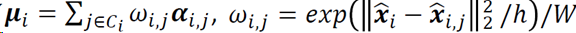
化简目标函数
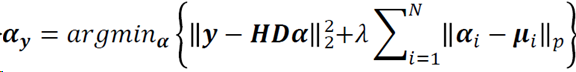
迭代解
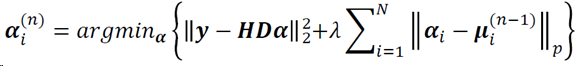
在NCSR方法中,考虑到稀疏表示噪声(SCN)普遍服从Laplacian分布,𝐿𝑝范数实际采用𝐿1范数
正则化参数𝜆由MAP估计原则自适应确定的。
使用局部自适应PCA字典,对图像块进行集群,对于每个集群,学习并使用PCA字典对集群中的图像块进行编码。
低秩最小化方法
思想
一组视觉信息通常具有低秩的固有属性。
例如:


联合稀疏
如何定义一组相关向量的稀疏度?
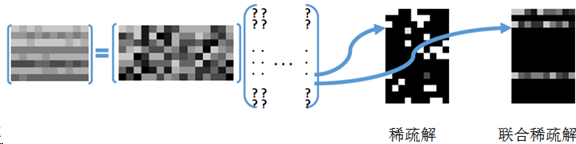
把一组图片视为二维低秩矩阵,秩为:
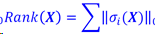
核范数最小化(NNM)
秩的最小化是非凸且NP困难问题,一个凸松弛形式是核范数:
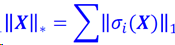
将一组图像组成的二维矩阵表示为:

其中Y每列表示一个图像样本,X为Y的理想低秩矩阵形式,E为残差矩阵。
核范数最小化(NNM)即一种从Y中估计X的方法,公式为:
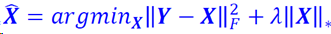
其解析解为:𝑿=𝑼𝑆𝜆(𝜮)𝑽𝑇
其中𝒀=𝑼𝜮𝑽𝑇(SVD分解),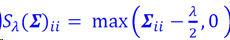
核范数最小化的缺陷在于对于所有奇异值都一视同仁,没有凸出奇异值大小的作用。
J.-F. Cai, E.J. Candèsand Z. Shen,A singular value thresholdingalgorithm for matrix completion,SIAM J. Optimiz., 20(4): 1956--1982, 2010.
加权奇异值最小化(WNNM)
加权核范数: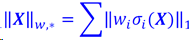
模型: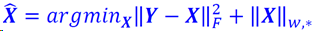
解为:
其中
S. Gu, Q. Xie, D. Meng, W. Zuo, X. Feng, L. Zhang, “Weighted Nuclear Norm Minimization and Its Applications to Low Level Vision,” International Journal of Computer Vision, 2017.
WNNM用于图像去噪
S. Gu, L. Zhang, W. Zuoand X. Feng, “Weighted Nuclear Norm Minimization with Application to Image Denoising,” CVPR 2014.
Robust PCA
一些应用中,残差矩阵E可能不服从高斯分布的,也可能是稀疏的。L1-范数在描述稀疏误差方面更稳健,模型为:
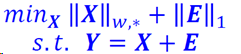
可以用ALM方法求解:
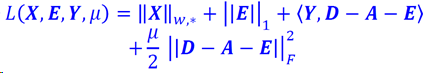
ALM方法
对于形如
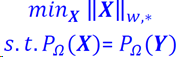
的目标函数,使用ALM方法,代价函数为
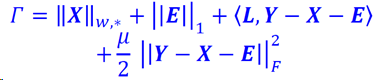
深度学习方法
Discriminative learning判别学习方法
从退化-潜在图像对(degraded-latent sample pairs)学习一个映射函数,通常公式采用如下形式:
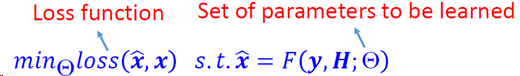
关键问题
合适的图像对训练数据集
模型结构
损失函数定义
基于模型的优化方法通常具有明确物理意义,但人工选择的先验条件(prior)可能不够准确,优化过程耗时较多,而判别学习方法实现数据驱动的端到端学习,学习好的模型的通用性和可解释性有限.
超分辨:
S. Gu, W. Zuo, Q. Xie, D. Meng, X. Feng, L. Zhang, "Convolutional Sparse Coding for Image Super-resolution," in ICCV 2015.
Dong, Chao, et al. "Image super-resolution using deep convolutional networks."IEEE PAMI 38.2 (2016): 295-307.
JiwonKim, Jung Kwon Lee, and KyoungMu Lee. "Accurate image super-resolution using very deep convolutional networks."CVPR, 2016.
WenzheShi, et al. "Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network."CVPR, 2016.
SRGAN:
C. Ledig, L. Theis, F. Huszar, J. Caballero, A. Cunningham, A. Acosta, A. Aitken, A. Tejani, J. Totz, Z. Wang, W. Shi, “Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network”, CVPR,2017
去噪:
K. Zhang, W. Zuo, Y. Chen, D. Meng, L. Zhang, "Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising,"IEEE Trans. on Image Processing, 2017.
Code: https://github.com/cszn/DnCNN
去模糊
Jiawei Zhang, et al. "Learning Fully Convolutional Networks for Iterative Non-blind Deconvolution."CVPR,2017.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号