交叉熵解读

参考：https://www.jianshu.com/p/8a0ad237b0ed

1、随机现象：并不总是出现相同结果的现象称为随机现象。

2、随机变量：随机现象各种结果的变量（一切可能的样本）称为随机变量。

3、信息量：概率越小的事件，信息量越大。

　 例如：

　　　　事件一：巴西进世界杯

　　　　事件二：中国进世界杯

　由于中国进世界杯的概率很小，所以事件二带来的信息量更大一些，给人留下的印象更深刻（惊讶）一些。

4、 用I表示信息量，P表示概率，两者之间的关系如下：                                            

　　　　　　　　　　　　　　　　　　I

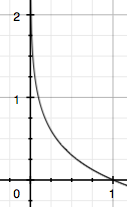                                                   P

信息量计算公式：

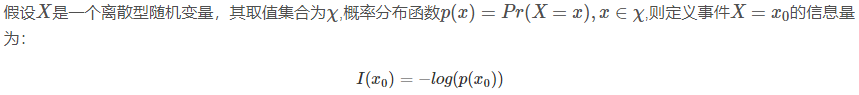
5、熵：所有信息量的期望值。例如，打开计算机有三种可能，具体如下表：

计算熵的公式：

　　　　　　

-log(p(xi))为每个信息量，-p(xi)logp(xi）为每个信息量占总事件的比例。假设一共有n个事件，即n个p(xi)log(p(xi))相加，前面加负号，使最后的值为正。

 

上面的例子，结合熵的定义，计算过程如下：

               

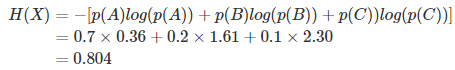
如果是二项分布，可以简化熵的计算。

              

6、相对熵（KL散度）：描述同一个随机变量的两个独立的概率分布的差异。

     如果有一个模型来表示一个样本，这个模型为P(x)。同时有另外一个模型Q（x）也可以表示这个样本。这两个模型也称为两个相互独立的概率分布P(x)和Q(x)，相对熵（KL散度）就是描述这两个分布（模型）的差异。

KL散度的计算公式：

                

n为样本所有可能的结果，Dkl的值越小，P分布（模型）和Q分布（模型）越接近。

7、交叉熵

     对上面的式子变形：

                

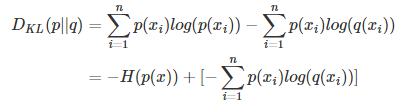
      等式的前一部分，恰好是P的熵的相反数，后一部分便是交叉熵。

 

                 

      在机器学习中需要评估label和precdicts的差距，使用KL散度恰好。KL散度前一部分是-H(p(x))不变，因此在优化过程中，只需关注KL散度的后一部分（交叉熵）即可，交叉熵越小，说明预测的模型和真实样本越匹配。