P4568 [JLOI2011] 飞行路线

分层图的板子题

代码

#include <bits/stdc++.h>
#define R(x) x=read()
#define fi first
#define se second
using namespace std;

typedef pair<int,int> PII;
const int N = 1e4, M = 5e5;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

struct EdgeElement{
    int toP, val, ne;
}edges[M*11+5];

int h[N*11+5];
int n, m, k, s, t;
int idx;

inline void add(int a, int b, int c)
{
    edges[++idx].toP = b;
    edges[idx].ne = h[a];
    edges[idx].val = c;
    h[a] = idx;
}

inline void addDouble(int a, int b, int c)
{
    add(a, b, c);
    add(b, a, c);
}

bool vis[N*11 + 5];
int dis[N*11 + 5];

int DJ()
{
    priority_queue<PII, vector<PII>, greater<PII> > Q;
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0;
    Q.push(make_pair(0, s));
    while(Q.size())
    {
        PII t = Q.top();
        Q.pop();
        if(vis[t.se])
            continue;
        for(int i = h[t.se]; i; i = edges[i].ne)
        {
            int j = edges[i].toP;
            if(dis[j] > dis[t.se] + edges[i].val)
            {
                dis[j] = dis[t.se] + edges[i].val;
                Q.push(make_pair(dis[j], j));
            }
        }
        vis[t.se] = 1;
    }
    return dis[t + n*k];
}

int main()
{
    // spots: 0~n-1
    R(n);R(m);R(k);
    R(s);R(t);
    for(int i = 1; i <= m; i++)
    {
        int a, b, c;
        R(a);R(b);R(c);
        addDouble(a, b, c);
        for(int j = 1; j <= k; j++)
        {
            addDouble(a + j * n, b + j * n, c);
            add(a + (j - 1) * n, b + j * n, 0);
            add(b + (j - 1) * n, a + j * n, 0);
        }
    }
    // attention!
    // additional operations about T
    for(int i = 1; i <= k; i++)
        add(t + (i-1)*n, t + i*n, 0);
    printf("%d\n", DJ());
    return 0;
}

细节

1.插入不同层之间的节点时，只能插入单向边，不能插双向边，以样例为例：

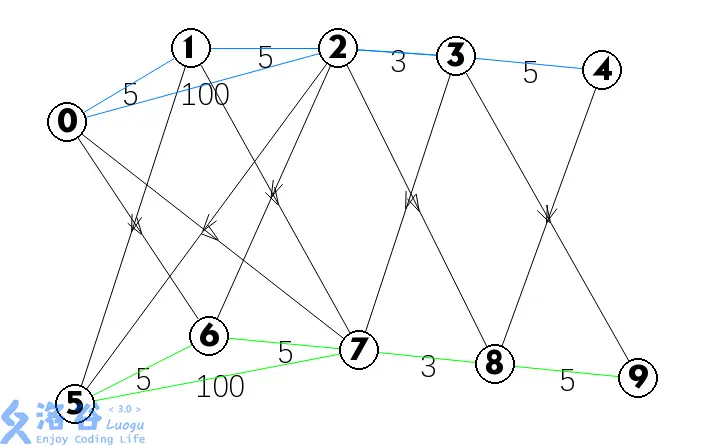
 如果在不同层之间插入的是双向边，那就可以从起点走免费点到下一层，然后又走免费边回来……

最后零成本到达终点。

2.边数M的确定

起初我是这样算M的：

题目中给的m上限是5e4，先乘以二，然后又因为要加上十层图，再乘以11.

for(int i = 1; i <= m; i++)
    {
        int a, b, c;
        R(a);R(b);R(c);
        addDouble(a, b, c);
        for(int j = 1; j <= k; j++)
        {
            addDouble(a + j * n, b + j * n, c);
            add(a + (j - 1) * n, b + j * n, 0);
            add(b + (j - 1) * n, a + j * n, 0);
        }
    }

我们可以看到，这里一次加了五条边，所以要再乘以5

3.终点的确定

for(int i = 1; i <= k; i++)
        add(t + (i-1)*n, t + i*n, 0);

因为我们这里把每一层的终点都连在一起了，所以可以直接把T+n*k作为终点；

如果没有进行这个操作的话，那就需要遍历每一层，dis[T+n*i]取min。