1655：数三角形

1655：数三角形

时间限制: 1000 ms         内存限制: 524288 KB
提交数: 90     通过数: 52

【题目描述】

给定一个 n×m

的网格，请计算三点都在格点上的三角形共有多少个。下图为 4×4

的网格上的一个三角形。

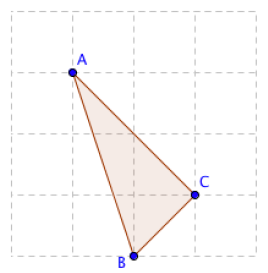
注意：三角形的三点不能共线。

【输入】

输入一行，包含两个空格分隔的正整数 m

和 n

。

【输出】

输出一个正整数，为所求三角形数量。

【输入样例】

2 2

【输出样例】

76

【提示】

数据范围与提示：

对于所有数据，1≤m,n≤1000

。

居然把图片也复制进来了吗。。。少说废话。

前面的题目基本都是水题而这道题需要动一下脑筋。

因为直接求三角形个数比较麻烦所以我们采取正难则反的方法

先求出所有的排列组合数，然后减去三点共线的情况

首先，一共有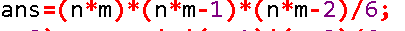这么多情况

然后三点都在同一条直线上的情况也比较好办

如果不进行判断的话可能会越减越大这个要注意

最后是重点，三点都在同一条斜线上（我已经把m和n先加了1）

解释下 以（0,0）为原点来枚举所有斜向上的斜线（因为矩形是对称的所以另一个方向不用考虑只要乘以2就行了）

去看看我上一篇blog的结论

然后每条先可以平移这么多次，再乘上就好了

 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m;
inline ll gcd(ll a,ll b)
{
    if(!b) return a;
    return gcd(b,a%b);
}
int main()
{
    scanf("%lld%lld",&m,&n);
    m++;
    n++;
    ll ans=(n*m)*(n*m-1)*(n*m-2)/6;
    if(n>2) ans-=m*n*(n-1)*(n-2)/6;
    if(m>2) ans-=n*m*(m-1)*(m-2)/6;
    for(int i=1;i<n;i++) 
     for(int j=1;j<m;j++)
      ans-=(gcd(i,j)-1)*(n-i)*(m-j)*2;
    printf("%lld",ans);
    return 0;
}