时间复杂度和空间复杂度1

目录

• 算法效率的度量方法
  • 事后统计方法
  • 事前分析估算方法
• 函数的将近增长
  • 定义

算法效率的度量方法

事后统计方法

通过设计好的测试程序和数据，利用计算机计时器对不用算法编制的程序的运行时间进行比较，从而确定算法的高低

缺陷：

1. 事先编制好程序，花费大量时间和精力
2. 时间的计算依赖计算机硬件和软件等环境因素
3. 算法的测试数据设计困境

事前分析估算方法

在计算程序编制前，依据统计方法对算法进行估算

取决因素：

1. 算法才用的策略、方法
2. 编译产生的代码质量
3. 问题输入规模
4. 机器执行指令速度

一个程序的运行时间，取决于算法的好坏和问题的输入规模(输入量的多少)

例子：

第一个算法：

int i, sum=0, n=100; //执行1次
for(i=0; i<=n; i++) // 执行n+1次
{
  sum = sum + i; //执行n次
}
prinf("%d", sum) //执行1次

第二种算法：

int sum = 0, n=100; //执行1次
sum = (1 + n) * n/2; //执行1次
printf("%d", sum); //执行1次

第一种算法执行了1 + (n +1)+ n+1 次 = 2n+3次

第二种算法执行 1 +1+1 = 3次

如果把循环看作一个整体，忽略头尾循环判断的开销，那么这个两个算法其实就是n次和1次的差距

例子：

int i,j, x=0, sum=0, n=100; //执行1次
for(i=1; i<=n; i++) 
{
  for(j=i; j<=n; j++) 
	{
    x++
  	sum = sum + x; 		//执行n * n次
  }
}
prinf("%d", sum) //执行1次

从这个例子中，i从1到100，每次都有让j循环100次，而当中x++ 和sum= sum+x；其实就是1+2+3+...+10000, 也就是100^{2次；循环整体n}2,显然算法执行次数与输入规模n=100有关系，算法执行时间随着n的增加也变长

因此，测试运行时间最可靠方法：计算对运行时间有消耗的基本操作次数；运行时间与这个计数成正比

我们不关心编写程序所用的编程设计语言是什么，不关心程序跑在什么计算机中，值关心实现算法，

不计哪些循环所用的递增和循环终止条件，变量声明，打印结果等操作，最终，在分析程序运行时间时，最重要的事把程序看成独立与程序设计语言的算法或以一系列步骤

分析一个算法的运行时间，重要的事基本操作的数量和输入规模关联起来，即基本操作的数量必须表示输入规模的函数

函数的将近增长

先判断两个算法A和B哪个更好？

前提：两个算法输入规模都是n

算法A：2n+3次操作

算法B：3n+1次操作

规模	算法A1（2n+3）	算法A2（2n）	算法B1（3n+1）	算法B2（3n）
n=1	5	2	4	3
n=2	7	4	7	6
n=3	9	6	10	9
n=10	23	20	31	30
n=100	203	200	301	300

分析：

• 当n=1时，算法A1效率不如算法B1
• 当n=2时，算法A1效率与算法B1相同
• 当n>2时，算法A1优于算法B1

总体上算法A比算法B优秀

定义

给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有n > N, f(n)总是比g(n)大，那么，我们说f(n)的增长渐近快于g(n)

第一个例子

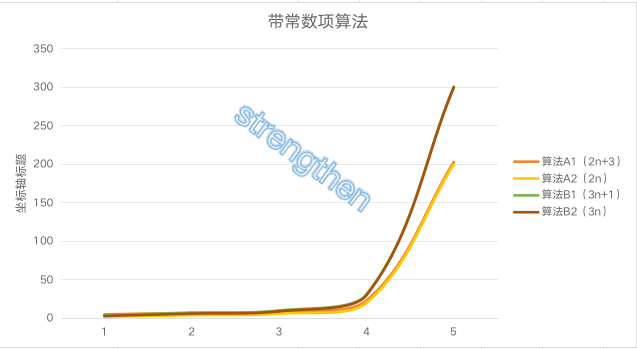
随着n的增大，算法后面+3和+1不会影响最终算法的变化，因此可以忽略这些算法的常数

第二个例子:

规模	算法C（4n+8）	算法C1（n）	算法D（2n^2+1）	算法D2（n^2）
n=1	12	1	3	1
n=2	16	2	9	4
n=3	20	3	19	9
n=10	48	10	201	100
n=100	408	100	20001	10000
n=1000	4008	1000	2000001	1000000

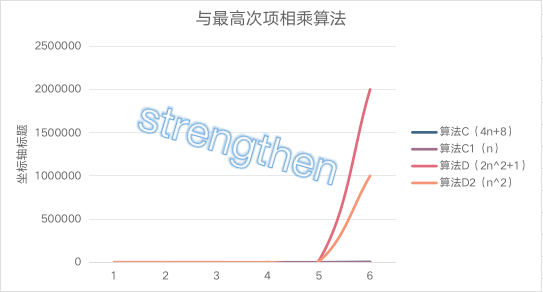
当n<=3时，算法C要差月算法D， 当n>3后，算法C的优势越来越优于算法D， 去掉与n相乘的常数,结果也没变化

,与最高次项相乘的常数并不重要

第三个例子：

算法E是 2n^2+3n+1, 算法F是2n^3+3n+1

规模	算法E(2n^2+3n+1)	算法E1(n^2)	算法F(2n^3+3n+1)	算法F2(n^3)
n=1	6	1	6	1
n=2	15	4	23	8
n=3	28	9	64	27
n=10	231	100	2031	1000
n=100	20301	10000	2000301	1000000

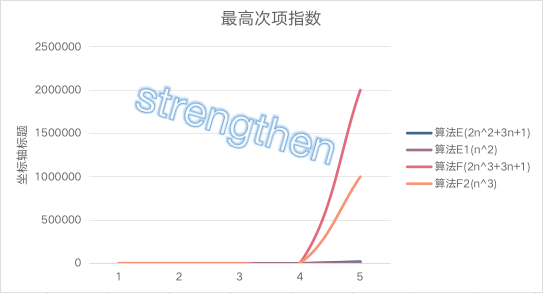
当n=1时，算法E与算法F结果相同

当n>1后，算法E优势就开始优于算法F，随着n的增大，差异非常明显

最高次项的指数大的，函数随着n的增大，结果也会变得增大特别快

最后一个例子

算法G：2n^2

算法H: 3n+1

算法I: 2n^2+3n+1

规模	算法G(2n^21)	算法H(3n+1)	算法I(2n^3+3n+1)
n=1	2	4	6
n=2	8	7	15
n=5	50	16	66
n=10	200	31	2031
n=100	20000	301	20301

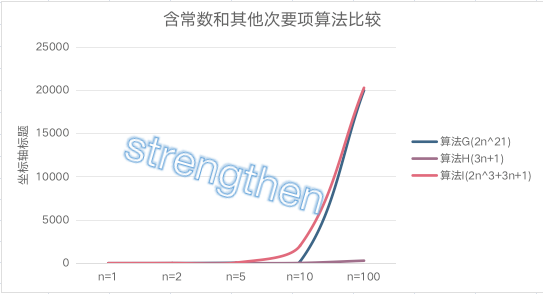
当n的值越来越大时，3n+1已经无法与2n^2比较，算法G的结果趋于算法I

判断一个算法效率时，函数中的常数和其他次要项常常可以忽略，更应该关注（最高阶项）的阶数

某个算法，随着n的增大，它会越来越优于另一个算法，或者越来越差另一个算法