如何快速设计一个FIR滤波器（二）通俗易懂，膜拜

一、理想低通滤波器单位脉冲响应是什么样

在如何快速设计一个FIR滤波器（一）中，我们介绍了一种简单设计FIR的方法——零极点法。这个方法非常简单，稍加培训，用笔和纸就能完成；当然缺点也很显而易见：零极点设计出的滤波器，只能给出大概的频率响应，对于一些要求较高的系统，显得无能为力。今天我们介绍一种更加严谨的方法。

现在假设我们要设计一个低通滤波器，截止频率为 $\omega_c$ ，其理想频率响应可以用如下函数表示：

$H_d(e^{j\omega})=\left\{ \begin{aligned} 1 ,\quad &\left| \omega \right| \leq \omega_c\\ 0, \quad& \left| \omega \right| >\omega_c \\ \end{aligned} \right.$

则该滤波器的脉冲响应为：

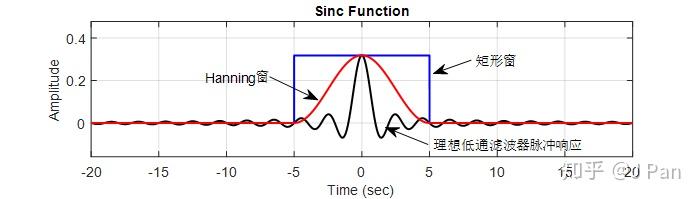
$h_d(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}H_d(e^{j\omega})e^{j\omega t}d\omega=\frac{sin(\omega_c t)}{\pi\omega_c}$

可见脉冲响应为一个sinc函数。画出来大概张这个样子：

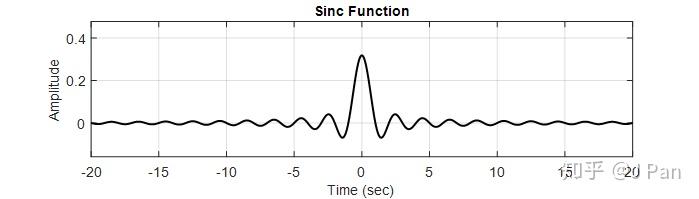
这个函数非常重要哦，建议都自己手动推导一下，非常有意思，我们把幅值最大的那一瓣称之为主瓣，剩下称之为从瓣，是不是很形象呢？注意主瓣的周期是从瓣的2倍哦。

可能你已经看见了，脉冲响应是由无穷多个——不对呀，我们是想设计一个有限脉冲响应的，结果出现了无穷多个响应，这可如何搞？——既然臣妾做不到把所有的脉冲响应都用上（因为我是有限脉冲滤波器FIR啊），那我只能截取有限一部分进行代替了，也就是——加窗。

窗函数这个东西很不好理解，我们就多花点功夫说说这个事。

二、什么是加窗

现在假设有一个函数，表达式为 $y(t)=Acos(2\pi f t)$ ，为简单起见，令 $A=1$ ， $f=1$ ，很显然，余弦函数的频域包含两个分量 $±f$ ，即 $±1$ Hz。

假如我们现在以10Hz的频率进行采样，显然是满足香浓采样定理的，采样脉冲及其频谱如下图：

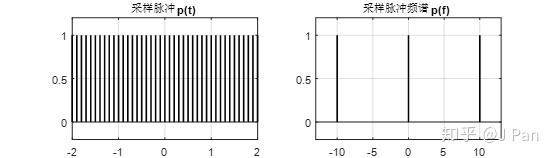
采样过程就是拿采样信号和原始信号进行乘积，那采样之后的信号长啥样呢？

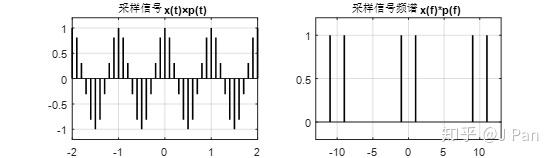
上图即为采样后的信号及其频谱。注意：此时采样后的信号是在时域无限扩展的，频谱也一样。但实际的计算中是不可能处理无穷多数量的信号的，那怎么办呢？——截短呗，只观察一部分样本行不？貌似我们也没有更好的选择了。

那怎么截短呢？最简单的方式就是矩形函数了，如下图所示：

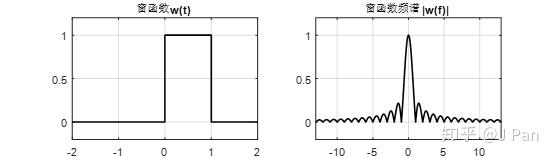
矩形函数的方法简单粗暴，只保留一部分（幅值为1），其余全部设为0，然后那矩形函数和采样信号相乘，就得到加窗（矩形窗）之后的采样信号了。矩形信号的频谱就是我们熟悉的sinc函数。加窗之后的采样信号及其频谱如下：

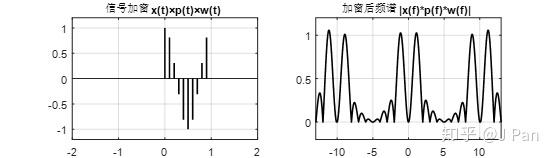
加窗后的离散余弦信号可以看成窗函数（矩形，频谱为sinc函数）与余弦离散信号的乘积。那在频域呢就是sinc函数和余弦频谱的卷积。看一个图就明白加窗后的频谱是怎么来的了：

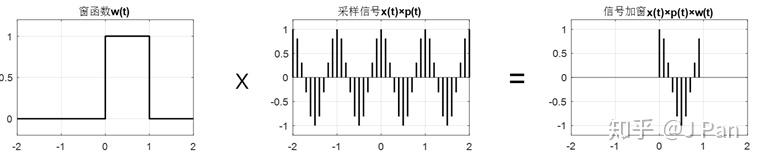
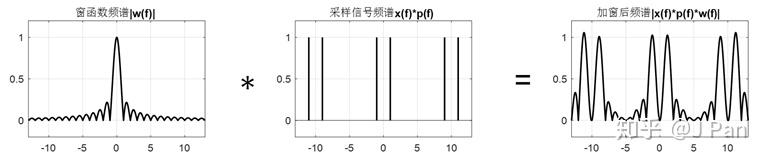
可以看出，由于加窗行为，频谱中频率成分变复杂了，由于矩形窗函数的频谱是无限宽的，在频谱的最大值处也出现了一定的畸变（略大于1）。这种有限长的离散信号在时域中计算机是可以处理（离散的），但是在频域还是不能，因为还是连续信号。在如何理解离散傅里叶变换及Z变换一文中，我们介绍了将有限长的信号进行周期延拓，就得到一个周期的离散信号，其傅里叶变换也是周期离散的，这样就可以在计算机中处理了。关于离散傅里叶变换，可以参照：

J Pan：如何理解离散傅里叶变换及Z变换zhuanlan.zhihu.com

现在问题就变成了如何进行周期延拓——卷积，什么意思呢？我们现在找一个采样脉冲，时域中周期和加窗后的采样信号的周期一致（都是1），其形貌如下图（左）所示：

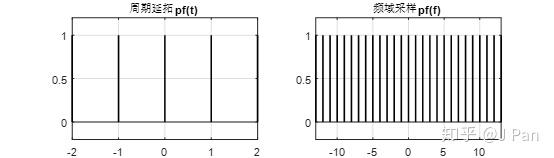
我们已经知道，周期延拓采样脉冲的频谱仍未采样脉冲如上图（右）所示。现在就可以做一个有意思的事情：周期延拓在数学上可以看成是一个有限长的信号（长度即为周期）和一个同样周期的无限长采样脉冲的卷积。什么意思呢？看一个图就一目了然了：

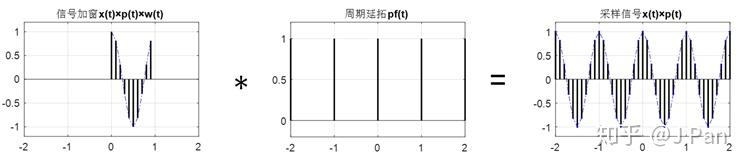
感兴趣的可以用卷积的数学定义推导一下看看是不是这样，很简单的。由卷积定理我们知道，卷积和乘积在时域和频域是对偶的，也就是说刚才我们所做的周期延拓（时域卷积）在频域是乘积哦，具体如下图所示。

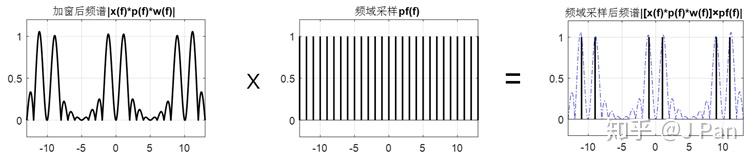
所以最终得到的经过周期延拓的加窗信号及其频谱如下图所示。可以看出，进过周期延拓，加窗导致的频谱泄漏似乎得到了抑制，加窗对频谱没什么影响。

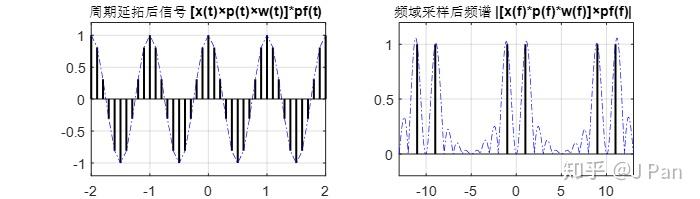
事实是不是这样呢？——直觉告诉我们应该不是。我们之所以最终得到这个结论，是因为我们选的初始函数太简单了。余弦函数是周期信号，频谱是有限宽度的，如果窗函数的宽度是信号周期的整数倍，则频域采样（时域周期延拓）将正好采在sinc函数的从瓣取值为零的地方，泄漏的频谱没有采到而已，具体如下图所示。

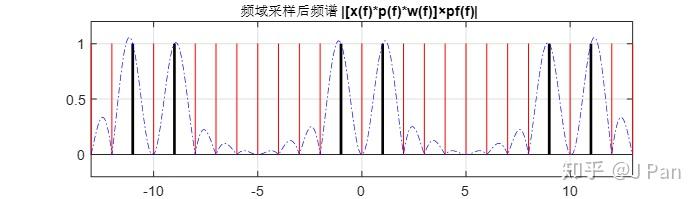
可能心细有童鞋会有疑问，为啥主瓣的最大值会有一定的偏移？——原因就是sinc函数主瓣和从瓣的周期不一样，卷积时主瓣与从半叠加，最大值就偏移了。

实际工程中，我们可能不知道被处理信号的周期，或者压根就不是周期的信号，那会出现什么呢？现在假如我们把窗函数加宽，比如增加到原来的1.4倍，如下图所示：

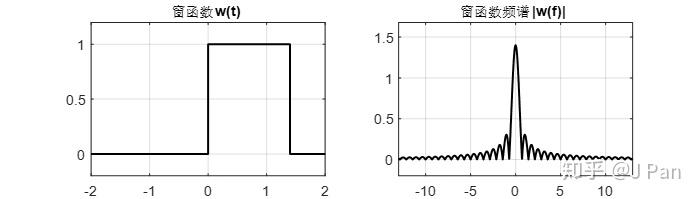
则可以得到加窗后的信号及频谱为：

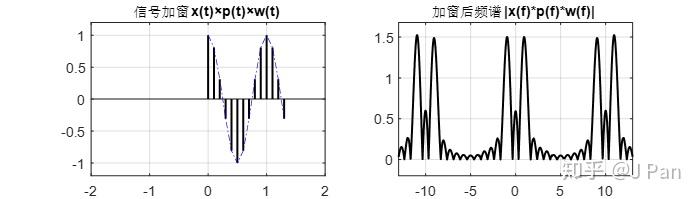
加窗并进行周期延拓后的信号及频谱为：

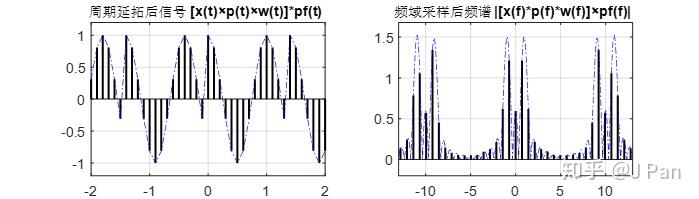
可见，由于窗函数宽度和原信号周期不一致，加窗后的信号进行周期延拓时出现了不连续，频域采样时不像前面那样只采集到sinc为零的地方，频谱出现了较大的泄漏，如下图所示。

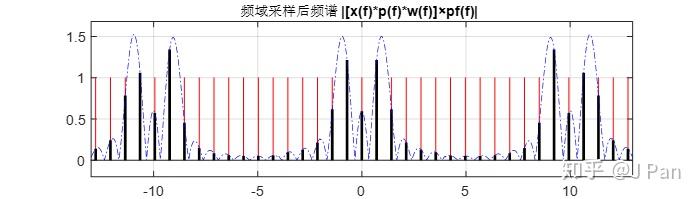
实际工程上绝大多数信号都不是周期信号，也不是有限长信号，而是我们只能观察有限长度而已。要想不出现频谱泄漏，需要窗函数长度是被处理信号频谱所有分量的整数倍，这几乎是不能达到的。因此加窗后，频谱泄漏是不可避免的，只能尽量减小。

本节中所用的算例来自离散傅里叶变换DFT基本原理图解，感兴趣请前往阅读。

三、窗函数都有哪些

最开始我们介绍了一个理想的低通滤波器，在频域内其幅值响应是一个矩形。这个矩形进行傅里叶逆变换，发现单位冲击响应有无穷多个，我们没办法，用了一个矩形窗进行截短，注意着两个矩形不是同一个事情哦，一个是幅值响应（频域），一个截短函数（时域），只不过样子都呈现矩形。

现在我们都放在频域来看：首先时域矩形函数在频域为sinc函数，时域的矩形函数截短（乘积）在频域对应卷积。也就是说在频域里，脉冲响应截短后的滤波器频域幅值响应是矩形信号和sinc信号的卷积，仔细想想这段话哦！下图展示了卷积之后的信号的样子。

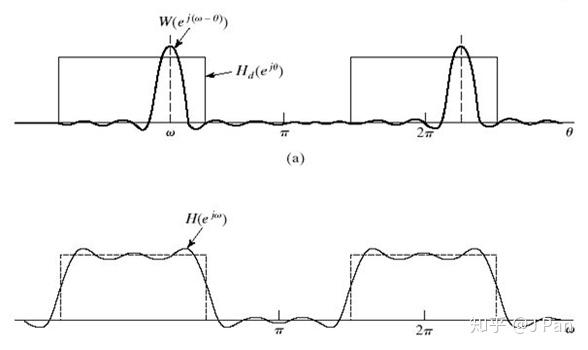
可以想象：假设窗函数宽度无穷大，则对应的sinc函数无穷窄，则卷积之后的函数非常接近理想矩形；反之，若窗函数很窄，在sinc函数就会变得很宽，则卷积之后的函数与理想矩形差别就比较大，这就是传说中的不确定原理哦，具体可参照：

J Pan：如何理解不确定性原理—不确定or测不准？zhuanlan.zhihu.com

那什么样的窗函数比较好呢？——在频域看就是要能量相对集中，也就是旁瓣要低。因为出现泄漏的主要原因就是窗函数的频谱是无限长的，与信号的频谱卷积时，主瓣与从瓣会出现叠加，因此从瓣的能量越小，影响就越小。在时域看就是加窗后的函数在进行周期延拓时尽量不要有非连续，因为非连续就需要很多分量来模拟，就造成了频谱泄露。那什么样函数的频谱主瓣能量较集中呢？——主要有以下是几种常见的窗函数：矩形窗、汉宁窗、汉明窗、凯撒窗等。

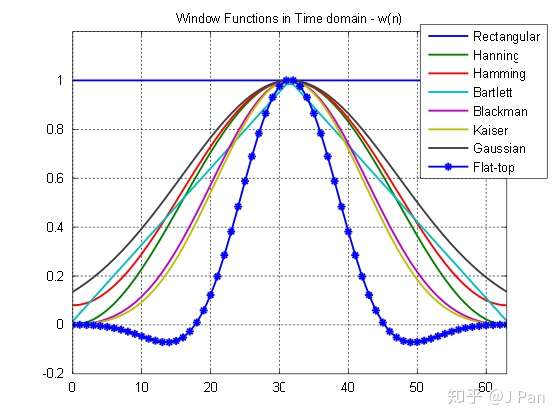
这些窗函数对应的频谱分别为：

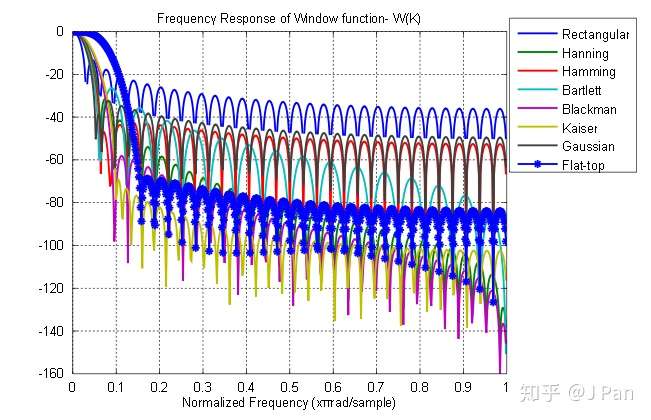
现在我们拿汉宁窗（Hanning）来举个例子。还是原来的余弦函数 $y(t)=Acos(2\pi f t)$ ， $A=1$ ， $f=1$ 。假设窗函数的宽度 $wT=1.4$ ，Hanning窗窗函数及其频谱为：

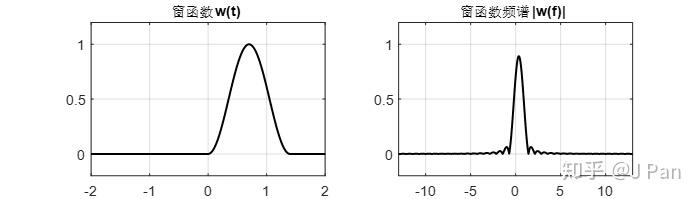
可见其频谱中主瓣能量与矩形窗比，集中了很多。余弦信号采样、加窗之后的信号及其频谱为：

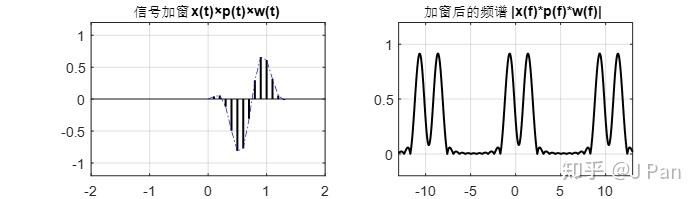
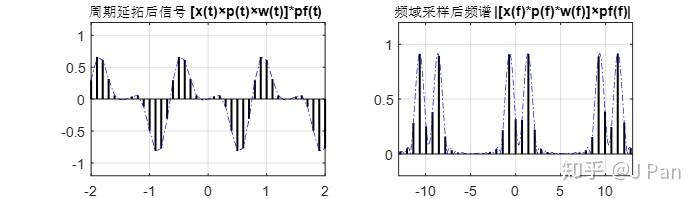
由于Hanning窗从零开始，结束的时候也是零，因此加窗之后的信号开始和结束也都是零，连续性好了，从频谱看，泄漏也少了。这个从周期延拓后（DTFT）的信号与频谱看的更清楚。

四、如何基于窗函数法设计FIR

这篇文章中，我们主要说怎么较为精确的设计一个FIR，我们花了大量篇幅说了窗函数，这是因为窗函数在实际的工程应用中很多，比如基于窗函数的FIR就是FIR设计中最广泛运用的一个方法。接下来，我们要介绍一下什么是用窗函数设计FIR。

在文章开始的时候，我们已经介绍了，对于理想低通滤波器，其脉冲响应为sinc函数，且有无穷多个，我们必须加窗才能处理，加窗就会有一定的频谱泄漏，因此实际设计出来的滤波器和理想滤波器还是有差别的。

基于窗函数的FIR设计就是通过选择合适常函数来找到满足要求的滤波器，一般步骤是这样的：

1）确定频域的响应函数 $H_d(e^{j\omega })$ ，低通、高通、带通或者其他；

2）确定频域的响应函数 $H_d(e^{j\omega })$ 的傅里叶逆变换，找到连续脉冲响应函数 $h_d(t)$ ；

3）对脉冲响应函数 $h_d(t)$ 按照一定的采样频率进行采样，获得离散信号 $h_d[m]$ ；

4）选择合适的窗函数，对离散信号 $h_d[m]$ 加窗，获得有限长度的脉冲响应 $h[m]$ ；

当然实际实践中，我们只需要知道这个过程，具体细节不需要我们考虑，因为MATLAB提供了一个强大的函数，帮我们都做好了——fir1。

fir1的基本语法如下：h = fir1(n,Wn,ftype,window)

其中n表示滤波器的阶数（order），Wn表示归一化后的滤波器的截止频率，可表示成 $[f_{low} \quad f_{high}]$ 的形式。举个例子，比如一个带状滤波器，采样频率 $f_s$ 是200Hz，两个截止频率分别为10Hz和50Hz，则 $[f_{low} \quad f_{high}]=[0.1 \quad 0.5]$ ，即截止频率除以 $\frac{1}{2}f_s$ 。ftype表示滤波器类型，可以是lowpass, highpass, bandpass, bandstop, or multiband filter。window表示窗函数类型，前面我们列到的窗函数都可以选择。h为所设计的滤波器的系数。

举个简单的例子：

h = fir1(48,[0.35 0.65]);
freqz(b,1,512)

这是一个48阶的带通滤波器，归一化的截止频率为[0.35 0.65]，其幅值响应和相位响应如下图所示。

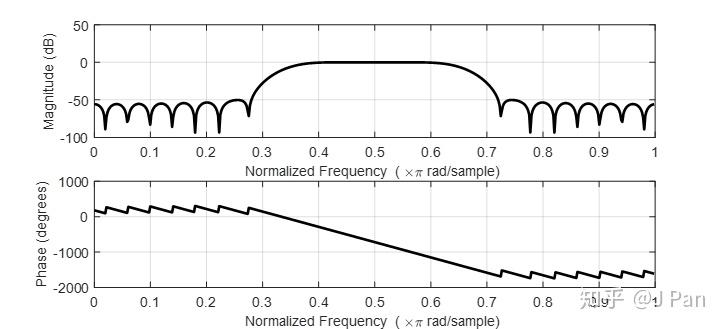
可见，采用fir1函数设计FIR滤波器非常方便。

除了fir1函数，fir2函数也有时候会用到，fir2函数是什么意思呢？——我们称之为基于频率采样法的设计方法，具体做法就是：把滤波器期望的幅值响应用一组分立的点 $(f_i,A(f_i)) \quad i=1,2,3,...M$ 来表示， $A(f_i)$ 表示频率为 $f_i$ 时的期望幅值响应，然后在不同的点之间进行线性插值，得到完成的期望幅值响应，然后进行傅里叶逆变换并用Hamming（汉明窗）截短来获得滤波器的系数。

基本语法为：h = fir2(n,f,m)

n表示滤波器阶数，f表示分离点的矢量，m表示分立点对应的幅值响应矢量，举个例子就明白了。现在要设计一个低通滤波器，幅值响应如下图所示：

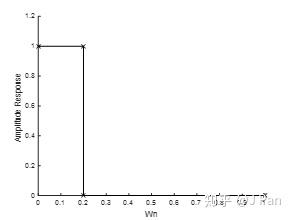
显然四个特征点的坐标分别为(0,1), (0.2,1), (0.2,0), (1,0) ，于是我们可以获得分立点的矢量为f=[0 0.2 0.2 1] ，对应幅值响应矢量为m=[1 1 0 0]。

f=[0 0.2 0.2 1] ;
m=[1 1 0 0];
h = fir2(48,f,m);
freqz(b,1)

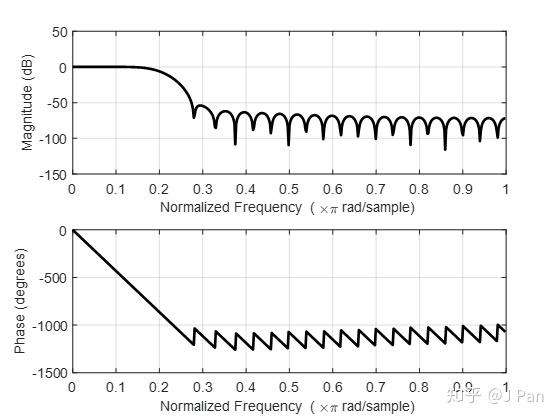
五、如何基于响应最优法设计FIR

前面我们说了两种基于窗函数的方法，主要是用窗函数对无限长的脉冲进行截短，获得近似的频域响应。除了窗函数法，还有另外的一种解决方案也比较常用，我们称之为“最优法”，主要思路就是找到一组脉冲响应，让它的频域响应 $H(e^{j\omega})$ 与期望的滤波器的频域响应 $H_d(e^{j\omega})$ 尽可能的一致，主要通过两种方法来实现，一个是最小二乘法，另一个是切比雪夫法。

（一）最小二乘法

与频率采样法近似，期望的频率响应用一组分立的点 $(f_i,A(f_i)) \quad i=1,2,3,...M$ 来表示，在不同的点之间进行插值，然后来寻找滤波器的系数 $\{h\}$ 时期满足

$\sum_{i=1}^{N}W_i\left[ H(f_i)-H_d(f_i) \right]^2\rightarrow min$

其中 $W_i$ 为不同频率下的权重。

MATLAB指令为：h=firls(n,f,m)

n为滤波器阶数，f表示分离点的矢量，m表示分立点对应的幅值响应矢量。仍以前面说的低通滤波器为例：

f=[0 0.2 0.2 1] ;
m=[1 1 0 0];
h = firls(48,f,m);
freqz(b,1)

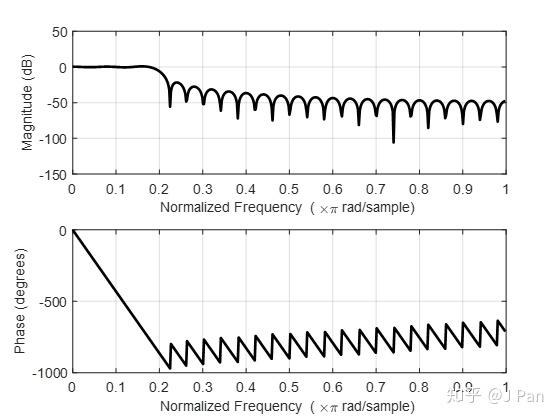
（二）切比雪夫法（又叫帕克斯-麦克劳林法）

与最小二乘法不同（方差最小），切比雪夫法采用的方案是最大误差最小，即：

$max\left| W_i\left( H(f_i)-H_d(f_i) \right) \right|\rightarrow min$

MATLAB指令为：h=firpm(n,f,m)

n、f、m定义和前面一致，不同的是频率响应在同一频率下必须去不同的值。前面的例子中当频率为0.2（归一化后）时，频率响应可直接从1降到0，对于切比雪夫法，规定不能这样做，我们将第二个0.2改为0,21。

f=[0 0.2 0.21 1] ;
m=[1 1 0 0];
h = firpm(48,f,m);
freqz(b,1)

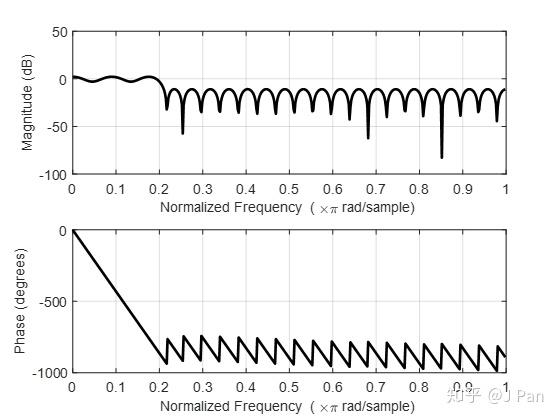
六、如何利用MATLAB设计FIR滤波器

要想快速设计一个FIR滤波器，MATLAB可以说是一个最有利的帮手，当你知道较多滤波器知识和相关函数时，可以直接调用函数进行设计，灵活且方便。当你不知道时，也没有关系，打开MATLAB，在命令行输入：filterDesigner或者fdatool(老版MATLAB)，你就能看到如下界面：

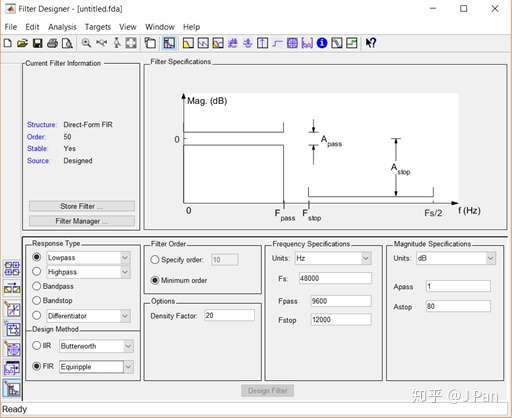
通过勾勾选选就能设计滤波器哦！

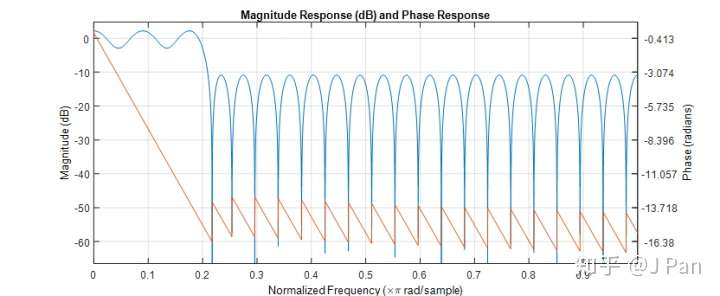
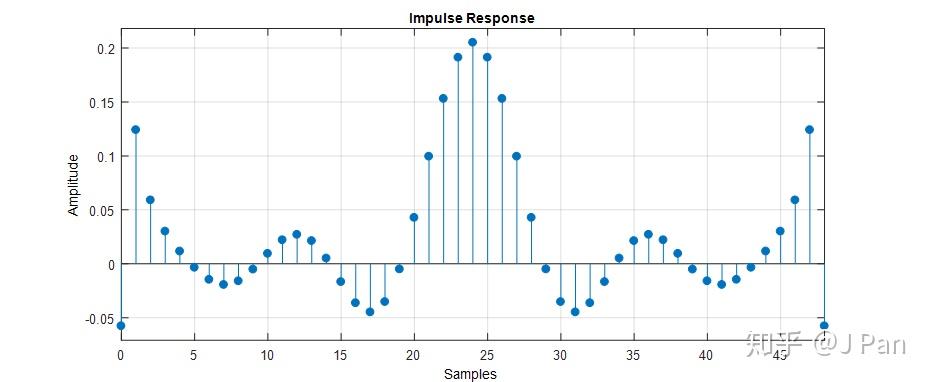
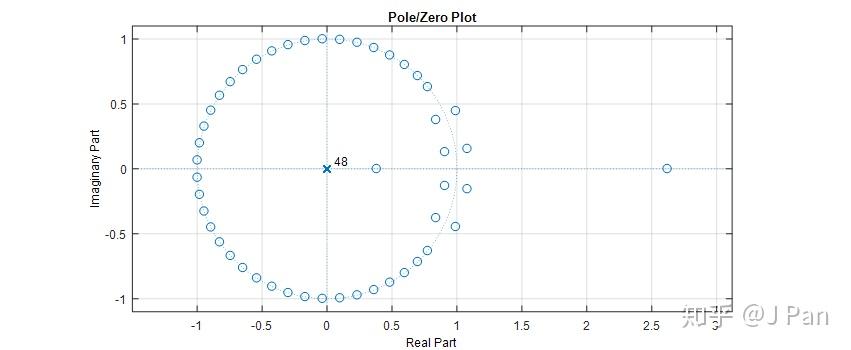
如果你又进步了一点，已经设计出一个滤波器，相看看性能怎么样，也简单，打开MATLAB，输入：fvtool(h)，h就是你设计的滤波器的系数，你就会看到各种你想要的滤波器特性：幅值响应、相位响应、脉冲响应、零极点等等。

转载在知乎——膜拜能把知识理解的怎么透彻

posted @ 2019-01-08 17:00 surferqing 阅读(2159) 评论(0) 编辑收藏举报

surferqing