[学习笔记]网络流
基本概念
网络流用来解决流量的问题:所有弧上流量的集合\(f={f(u,v)}\),称为该容量网络的一个网络流
- 带权的有向图\(G=(V,E)\) 满足以下几点,则称为网络流图
- 有一个入度为0的顶点\(s\),称\(s\)为源点。
- 有一个出度为0的顶点\(t\),称\(t\)为汇点。
- 每条边的权值为非负数,成为容量,记作\(c(i,j)\)。
- 弧的流量:通过容量网络\(G\)中每条弧\(<u,v>\),上的实际流量(简称流量),记为\(f(u,v)\);
- 对于任意一个时刻,设\(f(u,v)\)实际流量,则整个图\(G\)的流网络满足3个性质:
- 容量限制:对任意\(u,v∈V,f(u,v)≤c(u,v)\)。
- 反对称性:对任意\(u,v∈V,f(u,v) = -f(v,u)\)。从 \(u\)到\(v\)的流量一定是从\(v\)到\(u\)的流量的相反值。
- 流守恒性:对任意\(u\),若\(u\)不为\(S\)或\(T\),一定有\(∑f(u,v)=0,(u,v)∈E\)。即\(u\)到相邻节点的流量之和为0,因为流入\(u\)的流量和\(u\)点流出的流量相等,\(u\)点本身不会"制造"和"消耗"流量。
- 可行流:在容量网络\(G\)中满足以下条件的网络流\(f\),称为可行流:
- 弧流量限制条件: \(0<=f(u,v)<=c(u,v)\);
- 平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
- 零流 若网络流上每条弧上的流量都为0,则该网络流称为零流.
- 伪流:如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)
- 最大流最小割定理:
在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流. - 弧的类型:
- 饱和弧:即\(f(u,v)=c(u,v)\);
- 非饱和弧:即\(f(u,v) < c(u,v)\);
- 零流弧:即\(f(u,v)=0\);
- 非零流弧:即\(f(u,v)>0\).
- 最大流最小,可行流为最大流,当且仅当不存在新的增广路径。
- 链:在容量网络中,称顶点序列\((u_1,u_2,u_3,u_4,..,u_n,v)\)为一条链要求相邻的两个顶点之间有一条弧.
设\(P\)是\(G\)中一条从\(V_s\)到\(V_t\)的链,约定从\(V_s\)指向\(V_t\)的方向为正方向.在链中并不要求所有的弧的方向都与链的方向相同. - 割:
- 无向图的割集(Cut Set):\(C[A,B]\)是将图\(G\)分为\(A\)和\(B\)两个点集 \(A\)和\(B\)之间的边的全集
- 网络的割集:\(C[S,T]\)是将网络G分为\(s\)和\(t\)两部分点集 \(S\)属于\(s\)且\(T\)属于\(t\) 从\(S\)到\(T\)的边的全集
- 带权图的割(Cut):就是割集中边或者有向边的权和
- 增广路:如果一个可行流不是最大流,那么当前网络中一定存在一条增广路,通过该条路径\(p\)使得图\(G\)的最大流得到了增加,这样的路径\(p\)被称为增广路径。
- 残留容量
给定容量网络\(G(V,E)\),及可行流\(f\),弧\(<u,v>\)上的残留容量记为\(cl(u,v)=c(u,v)-f(u,v)\).每条弧上的残留容量表示这条弧上可以增加的流量.因为从顶点\(u\)到顶点\(v\)的流量减少,等效与从顶点\(v\)到顶点\(u\)的流量增加,所以每条弧\(<u,v>\)上还有一个反方向的残留容量\(cl(v,u)=-f(u,v)\). - 残余网络 (Residual Network)
在一个网络流图上,找到一条源到汇的路径(即找到了一个流量)后,对路径上所有的边,其容量都减去此次找到的量,对路径上所有的边,都添加一条反向边,其容量也等于此次找到的流量,这样得到的新图,就称为原图的“残余网络”. - 费用流 即在网络流的基础上,每条边都加上了费用,网络的费用等于该边的费用乘以流量。
常用算法
最大流算法
引入反向边 为什么要有反向边?

我们第一次找到了\(1-2-3-4\)这条增广路,这条路上的$ Delta$值显然是\(1\)。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候\((1,2)\)和\((3,4)\)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是\(1\)。
但这个答案明显不是最大流,因为我们可以同时走\(1-2-4\)和\(1-3-4\),这样可以得到流量为\(2\)的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走\((2-3-4)\)而改走\((2-4)\)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边\((i,j)\)都有一条反向边\((j,i)\),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少\(Delta\)的同时,也把每一段上的反方向的容量增加\(Delta\)。即在\(Dec(c[x,y],Delta)\)的同时,\(inc(c[y,x],Delta)\)
我们来看刚才的例子,在找到\(1-2-3-4\)这条增广路之后,把容量修改成如下
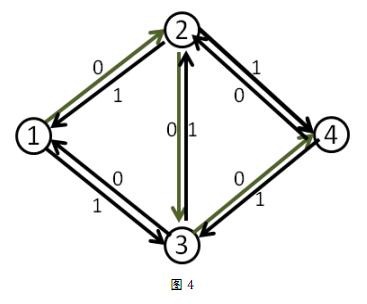
这时再找增广路的时候,就会找到\(1-3-2-4\)这条可增广量,即\(Delta\)值为\(1\)的可增广路。将这条路增广之后,得到了最大流\(2\)。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走\(3-2\)这条反向边的时候,就相当于把\(2-3\)这条正向边已经是用了的流量给”退”了回去,不走\(2-3\)这条路,而改走从\(2\)点出发的其他的路也就是\(2-4\)。(有人问如果这里没有\(2-4\)怎么办,这时假如没有\(2-4\)这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在\(3-4\)上的流量由\(1-3-4\)这条路来”接管”。而最终\(2-3\)这条路正向流量\(1\),反向流量\(1\),等于没有流量。
最大流入门题
- 题目描述
Every time it rains on Farmer John's fields, a pond forms over Bessie's favorite clover patch. This means that the clover is covered by water for awhile and takes quite a long time to regrow. Thus, Farmer John has built a set of drainage ditches so that Bessie's clover patch is never covered in water. Instead, the water is drained to a nearby stream. Being an ace engineer, Farmer John has also installed regulators at the beginning of each ditch, so he can control at what rate water flows into that ditch.
Farmer John knows not only how many gallons of water each ditch can transport per minute but also the exact layout of the ditches, which feed out of the pond and into each other and stream in a potentially complex network. Note however, that there can be more than one ditch between two intersections.
Given all this information, determine the maximum rate at which water can be transported out of the pond and into the stream. For any given ditch, water flows in only one direction, but there might be a way that water can flow in a circle.
- 输入
Line 1: Two space-separated integers, N (0 <= N <= 200) and M (2 <= M <= 200). N is the number of ditches that Farmer John has dug. M is the number of intersections points for those ditches. Intersection 1 is the pond. Intersection point M is the stream.
Line 2..N+1:Each of N lines contains three integers, Si, Ei, and Ci. Si and Ei (1 <= Si, Ei <= M) designate the intersections between which this ditch flows. Water will flow through this ditch from Si to Ei. Ci (0 <= Ci <= 10,000,000) is the maximum rate at which water will flow through the ditch.
- 输出
One line with a single integer, the maximum rate at which water may be emptied from the pond.
- 样例输入
5 4
1 2 40
1 4 20
2 4 20
2 3 30
3 4 10
- 样例输出
50
EK算法:
- 算法流程如下:
设队列Q:存储当前未访问的节点,队首节点出队后,成为已检查的标点;
Path数组:存储当前已访问过的节点的增广路径;
Flow数组:存储一次BFS遍历之后流的可改进量;
Repeat:
Path清空;
源点S进入Path和Q,Path[S]<-0,Flow[S]<-+∞;
While Q非空 and 汇点T未访问 do
Begin
队首顶点u出队;
For每一条从u出发的弧(u,v) do
If v未访问 and 弧(u,v) 的流量可改进;
Then Flow[v]<-min(Flow[u],c[u][v]) and v入队 and Path[v]<-u;
End while
If(汇点T已访问)
Then 从汇点T沿着Path构造残余网络;
Until 汇点T未被访问
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=210;
const int inf=0x3f3f3f3f;
int n,m,mapp[maxn][maxn],path[maxn],flow[maxn],st,en;
queue<int>q;
template<class T>
void read(T &res){
res=0;
T f=1;
char c;
c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
res=res*10+c-'0';
c=getchar();
}
res*=f;
}
int bfs(){
int t;
while(!q.empty()) q.pop();
memset(path,-1,sizeof(path));
path[st]=0,flow[st]=inf;
q.push(st);
while(!q.empty()){
t=q.front();
q.pop();
if(t==en) break;
for(int i=1;i<=m;i++){
if(i!=st&&path[i]==-1&&mapp[t][i]){
flow[i]=flow[t]<mapp[t][i]?flow[t]:mapp[t][i];//汇入该点的流可改进
q.push(i);
path[i]=t;//增广路径
}
}
}
if(path[en]==-1) return -1;
return flow[m];//流量可改进
}
int ek(){
int max_flow=0,step,now,pre;
while((step=bfs())!=-1){//没有增广路径说明是最大流
max_flow+=step;
now=en;
while(now!=st){//构造残余网络
pre=path[now];
mapp[pre][now]-=step;
mapp[now][pre]+=step;//反向边
now=pre;
}
}
return max_flow;
}
int main(){
int u,v,cost;
while(scanf("%d %d",&n,&m)!=EOF){
memset(mapp,0,sizeof(mapp));
for(int i=1;i<=n;i++){
read(u);
read(v);
read(cost);
mapp[u][v]+=cost;
}
st=1,en=m;
printf("%d\n",ek());
}
return 0;
}
实际上EK算法并不是很优 最好使用的是dinic算法
Dinic算法
Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=300;
const int inf=0x3f3f3f3f;
template<class T>
void read(T &res){
res=0;
T f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
res=res*10+c-'0';
c=getchar();
}
res*=f;
}
struct Edge
{
int next,val,to;
}e[maxn<<1];
int head[maxn],dep[maxn],n,m,tol=1,ans;
inline void add(int u,int v,int val)
{
tol++;
e[tol].to=v;
e[tol].next=head[u];
e[tol].val=val;
head[u]=tol;
}
bool bfs(int s,int t){
queue<int>q;//定义一个bfs寻找分层图时的队列
memset(dep,-1,sizeof(dep));
q.push(s);
dep[s]=0;//源点深度为0
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=head[now];i;i=e[i].next){
if(dep[e[i].to]==-1&&e[i].val){//若该残量不为0,且to还未分配深度,则给其分配深度并放入队列
dep[e[i].to]=dep[now]+1;
if(e[i].to==t) return true;
q.push(e[i].to);
}
}
}
return false;
}
int dfs(int x,int maxx){//u是当前节点,maxx是当前流量
if(x==m) return maxx;
for(int i=head[x];i;i=e[i].next){
if(dep[e[i].to]==dep[x]+1&&e[i].val>0){//注意这里要满足分层图和残量不为0两个条件
int flow=dfs(e[i].to,min(maxx,e[i].val));//向下增广
if(flow){//若增广成功
e[i].val-=flow;//正向边减
e[i^1].val+=flow;//反向边加,有个小技巧
return flow;//向上传递
}
}
}
return 0;//否则说明没有增广路,返回0
}
void dinic(int s,int t)
{
while(bfs(s,t)) ans+=dfs(s,inf);
}
int main(){
read(n);
read(m);
int u,v,cost;
for(int i=1;i<=n;i++){
read(u);
read(v);
read(cost);
add(u,v,cost);
add(v,u,0);
}
dinic(1,m);
printf("%d\n",ans);
return 0;
}
当前弧优化
即每一次dfs增广时不从第一条边开始,而是用一个数组cur记录点u之前循环到了哪一条边,以此来加速
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=300;
const int inf=0x3f3f3f3f;
template<class T>
void read(T &res){
res=0;
T f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
res=res*10+c-'0';
c=getchar();
}
res*=f;
}
struct Edge
{
int next,val,to;
}e[maxn<<1];
int head[maxn],dep[maxn],n,m,tol=1,ans;
int cur[maxn];//cur就是记录当前点u循环到了哪一条边
int src,sink;
inline void add(int u,int v,int val)
{
tol++;
e[tol].to=v;
e[tol].next=head[u];
e[tol].val=val;
head[u]=tol;
}
bool bfs(int s,int t){
queue<int>q;//定义一个bfs寻找分层图时的队列
memset(dep,-1,sizeof(dep));
q.push(s);
dep[s]=0;//源点深度为0
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=head[now];i;i=e[i].next){
if(dep[e[i].to]==-1&&e[i].val){//若该残量不为0,且to还未分配深度,则给其分配深度并放入队列
dep[e[i].to]=dep[now]+1;
if(e[i].to==t) return true;
q.push(e[i].to);
}
}
}
return false;
}
int dfs(int x,int maxx){//u是当前节点,dist是当前流量
if(x==sink) return maxx;
for(int& i=cur[x];i;i=e[i].next){//注意这里的&符号,这样i增加的同时也能改变cur[u]的值,达到记录当前弧的目的
if(dep[e[i].to]==dep[x]+1&&e[i].val>0){//注意这里要满足分层图和残量不为0两个条件
int flow=dfs(e[i].to,min(maxx,e[i].val));//向下增广
if(flow){//若增广成功
e[i].val-=flow;//正向边减
e[i^1].val+=flow;//反向边加
return flow;//向上传递
}
}
}
return 0;//否则说明没有增广路,返回0
}
void dinic(int s,int t)
{
ans=0;
while(bfs(s,t)){
for(int i=0;i<=n;i++) cur[i]=head[i];//每一次建立完分层图后都要把cur置为每一个点的第一条边
while(int d=dfs(s,inf)) ans+=d;
}
}
int main(){
read(n);
read(m);
int u,v,cost;
for(int i=1;i<=n;i++){
read(u);
read(v);
read(cost);
add(u,v,cost);
add(v,u,0);
}
dinic(1,m);
printf("%d\n",ans);
return 0;
}
模板
const int maxn=1e5+7;
const int maxm=1e5+7;
const int inf=0x3f3f3f3f;
struct Dinic {
struct Edge {
int next, f, to;
} e[maxm];
int head[maxn], dep[maxn], tol, ans;
int cur[maxn];
int src, sink, n;
void add(int u, int v, int f) {
tol++;
e[tol].to = v;
e[tol].next = head[u];
e[tol].f = f;
head[u] = tol;
tol++;
e[tol].to = u;
e[tol].next = head[v];
e[tol].f = 0;
head[v] = tol;
}
bool bfs() {
queue<int> q;
memset(dep, -1, sizeof(dep));
q.push(src);
dep[src] = 0;
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = head[now]; i; i = e[i].next) {
if (dep[e[i].to] == -1 && e[i].f) {
dep[e[i].to] = dep[now] + 1;
if (e[i].to == sink)
return true;
q.push(e[i].to);
}
}
}
return false;
}
int dfs(int x, int maxx) {
if (x == sink)
return maxx;
for (int &i = cur[x]; i; i = e[i].next) {
if (dep[e[i].to] == dep[x] + 1 && e[i].f > 0) {
int flow = dfs(e[i].to, min(maxx, e[i].f));
if (flow) {
e[i].f -= flow;
e[i ^ 1].f += flow;
return flow;
}
}
}
return 0;
}
int dinic(int s, int t) {
ans = 0;
this->src = s;
this->sink = t;
while (bfs()) {
for (int i = 0; i <= n; i++)
cur[i] = head[i];
while (int d = dfs(src, inf))
ans += d;
}
return ans;
}
void init(int n) {
this->n = n;
memset(head, 0, sizeof(head));
tol = 1;
}
} G;
最小费用最大流
刚好有一道比较基础的题目。这题主要是难在建图。每部动画只能供一个人看,有k个人,连续看重复的动画会损失幸福感。怎样让幸福感最大?
如何连边?有一个超级大源点,再设一个起点,源点到起点的最大流量是k,每部动画拆成两个点,两点价值刚好为这部动画的幸福感的负数,因为要求最小花费,所以把边权用负数就好了。然后除起点,每条边的最大流量为1,这样就保证了每部动画只有一个人看。然后直接套模板就好了
#include <bits/stdc++.h>
using namespace std;
const int maxn = 500010;
const int maxm = 500010;
const int INF = 0x3f3f3f3f;
template<class T>
void read(T &res){
res=0;
T f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
res=res*10+c-'0';
c=getchar();
}
res*=f;
}
struct edge
{
int to,next,cap,flow,cost;
}e[maxn];
int head[maxn],tol;
int pre[maxn],dis[maxn];
bool vis[maxn];
int N;
void init(int n)
{
N=n;
tol=1;
memset(head,0,sizeof(head));
}
void addedge(int u,int v,int cap,int cost)
{
tol++;
e[tol].to=v;
e[tol].cap=cap;
e[tol].cost=cost;
e[tol].flow=0;
e[tol].next=head[u];
head[u]=tol;
tol++;
e[tol].to=u;
e[tol].cap=0;
e[tol].flow=0;
e[tol].cost=-cost;
e[tol].next=head[v];
head[v]=tol;
}
bool spfa(int s,int t)
{
queue<int>q;
for(int i=0;i<=N;i++){
dis[i]=INF;
vis[i]=false;
pre[i]=-1;
}
dis[s]=0;
vis[s]=true;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=false;
for(int i=head[u];i;i=e[i].next)
{
int v= e[i].to;
if( e[i].cap>e[i].flow&&dis[v]>dis[u]+e[i].cost){
dis[v]=dis[u]+e[i].cost;
pre[v]=i;
if(!vis[v]){
vis[v]=true;
q.push(v);
}
}
}
}
if(pre[t]==-1) return false;
else return true;
}
int cost=0;
int mcmf(int s,int t)
{
int flow=0;
cost=0;
while(spfa(s,t)){
int minn=INF;
for(int i=pre[t];i!=-1;i=pre[e[i^1].to]){
if(minn> e[i].cap- e[i].flow){
minn=e[i].cap- e[i].flow;
}
}
for(int i=pre[t];i!=-1;i=pre[e[i^1].to]){
e[i].flow+=minn;
e[i^1].flow-=minn;
cost+=e[i].cost*minn;
}
flow+=minn;
}
return flow;
}
struct node
{
int l,r,val,op;
}s[300];
bool cmp(node a,node b)
{
if(a.l==b.l) return a.r<b.r;
else return a.l<b.l;
}
int main()
{
//freopen("in.txt","r",stdin);
int t,m,n,k,w;
read(t);
while(t--){
read(n);
read(m);
read(k);
read(w);
init(m*2+3);
addedge(0,1,k,0);
for(int i=1;i<=m;i++){
read(s[i].l);
read(s[i].r);
read(s[i].val);
read(s[i].op);
addedge(i+m+1,m*2+2,1,0);//拆点 第二个点连汇点
}
sort(s+1,s+m+1,cmp);
for(int i=1;i<=m;i++){
addedge(i+1,i+m+1,1,-s[i].val);
}
for(int i=1;i<=m;i++){
addedge(1,i+1,1,0);
}
for(int i=1;i<=m;i++){
for(int j=1;j<=m;j++){
if(i!=j){
if(s[j].l>=s[i].r){
if(s[i].op==s[j].op){
addedge(i+m+1,j+1,1,w);
}
else{
addedge(i+m+1,j+1,1,0);//一点的第二个点连一点的第一个点
}
}
}
}
}
mcmf(0,m*2+2);
printf("%d\n",(-cost));
}
//fclose(stdin);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号